3.8: La Métrica en la Relatividad General

Hasta ahora hemos considerado una variedad de ejemplos en los que la métrica está predeterminada. No es así en la relatividad general. Por ejemplo, Einstein publicó la relatividad general en 1915, pero no fue hasta 1916 cuando Schwarzschild encontró la métrica para un cuerpo esférico, gravitante como el sol o la tierra.

Cuando hay masas presentes, encontrar la métrica es análogo a encontrar el campo eléctrico hecho por cargas, pero la interpretación es más difícil. En el caso electromagnético, el campo se encuentra sobre un fondo preexistente de espacio y tiempo. En la relatividad general, no hay geometría preexistente del espacio-tiempo. La métrica nos dice cómo encontrar distancias en términos de nuestras coordenadas, pero las coordenadas en sí mismas son completamente arbitrarias. Entonces, ¿qué significa incluso la métrica? Este fue un tema que causó gran angustia y confusión a Einstein, y en un momento dado, en 1914, incluso lo llevó a publicar una teoría incorrecta y sin salida de la gravedad en la que abandonó la independencia de coordenadas.

Con el beneficio de la retrospectiva, podemos considerar estos temas en términos de la descripción general de las mediciones en relatividad dada en la sección 3.4:

1. Podemos decir si los eventos y las líneas mundiales son incidentes.
2. Podemos hacer mediciones en marcos locales de Lorentz.

El argumento del agujero

El principal factor que llevó a Einstein a su falso inicio se conoce como el argumento del agujero. Supongamos que conocemos la distribución de la materia a lo largo de todo el espacio-tiempo, incluyendo una región particular de tamaño finito —el “agujero ”— que no contiene materia. Por analogía con otras teorías clásicas de campo, como el electromagnetismo, esperamos que la métrica sea una solución a algún tipo de ecuación diferencial, en la que la materia actúa como término fuente. Encontramos una métrica\(g(x)\) que resuelve las ecuaciones de campo para este conjunto de fuentes, donde\(x\) hay algún conjunto de coordenadas. Ahora bien, si las ecuaciones de campo son independientes de coordenadas, podemos introducir un nuevo conjunto de coordenadas x', que es idéntico al\(x\) exterior del agujero, pero difiere de él en el interior. Si reexpresamos la métrica en términos de estas nuevas coordenadas como\(g'(x')\), entonces se nos garantiza que también\(g'(x')\) es una solución. Pero además, podemos sustituir\(x\)\(x'\), y\(g'(x)\) seguirá siendo una solución. Para el exterior del agujero no hay diferencia entre las cantidades cebadas y no cebadas, y dentro del agujero no hay una distribución de masa que tenga que coincidir con el comportamiento de la métrica punto por punto.

Figura\(\PageIndex{1}\) - Argumento del agujero de Einstein.

Concluimos que en cualquier teoría de coordenadas invariantes, es imposible determinar de manera única la métrica dentro de dicho agujero. Einstein inicialmente decidió que esto era inaceptable, porque mostraba una falta de determinismo; en una teoría clásica como la relatividad general, debemos ser capaces de predecir la evolución de los campos, y parecería que no hay forma de predecir la métrica dentro del agujero. Finalmente se dio cuenta de que se trataba de una interpretación incorrecta. El único tipo de observación global que la relatividad general nos permite hacer son las mediciones de la incidencia de las líneas mundiales. Volver a etiquetar todos los puntos dentro del agujero no cambia ninguna de las relaciones de incidencia. Por ejemplo, si dos partículas de prueba enviadas a la región chocan en un punto x dentro del agujero, entonces cambiar el nombre del punto a x' no cambia el hecho observable de que colisionaron.

Una paradoja maquiana

Otro tipo de argumento que hizo sufrir a Einstein también se resuelve mediante una correcta comprensión de las mediciones, esta vez el uso de mediciones en marcos locales de Lorentz. La tierra se encuentra en equilibrio hidrostático, y su ecuador sobresale debido a su rotación. Supongamos que el universo estaba vacío a excepción de dos planetas, cada uno girando alrededor de la línea que conecta sus centros. ¹³ Al no existir estrellas u otros puntos de referencia externos, los habitantes de cada planeta no tienen puntos de referencia externos contra los que juzgar su rotación o falta de rotación. Sólo pueden determinar su rotación, dijo Einstein, en relación con el otro planeta. Ahora supongamos que un planeta tiene un bulto ecuatorial y el otro no, esto parece violar el determinismo, ya que no hay causa que pueda producir el efecto diferente. Las personas de cualquiera de los dos planetas pueden considerarse a sí mismas como giratorias y al otro planeta como estacionarias, o pueden describir la situación al revés. Einstein creía que este argumento demostraba que no podía haber diferencia entre los tamaños de los bultos ecuatoriales de los dos planetas.

Figura\(\PageIndex{2}\) - ¿Una paradoja? El planeta A no tiene protuberancia ecuatorial, pero B sí. ¿Qué causa produce este efecto? Einstein razonó que la causa no podía ser la rotación de B, porque cada planeta gira en relación con el otro.

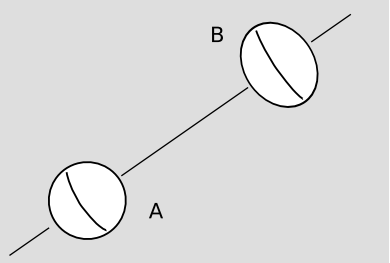
Nota

El ejemplo se describe en la ponencia de Einstein “La Fundación de la Teoría General de la Relatividad”. Un extracto, que incluye el ejemplo, se da en el Apéndice A.

La falla en el argumento de Einstein fue que las mediciones en los marcos locales de Lorentz sí permiten hacer una distinción entre rotación y falta de rotación. Por ejemplo, supongamos que los científicos del planeta A notan que su mundo no tiene protuberancia ecuatorial, mientras que el planeta B tiene uno. Mandan una sonda espacial con un reloj a B, dejan que permanezca en la superficie de B por algunos años, y luego ordenan que regrese. Cuando el reloj está de vuelta en el laboratorio, lo comparan con otro reloj que permaneció en el laboratorio en el planeta A, y encuentran que ha transcurrido menos tiempo de acuerdo con el que pasó el tiempo en la superficie de B. Concluyen que el planeta B está rotando más rápidamente que el planeta A, y que el movimiento de la superficie de B fue la causa de la dilatación del tiempo observada. Esta resolución de la aparente paradoja depende específicamente de la forma lorentziana de la geometría local del espacio-tiempo; no está disponible, por ejemplo, en la descripción curva espacio-temporal de Cartan de la gravedad newtoniana.

El uso original e incorrecto de Einstein de este ejemplo surgió de su interés por las ideas del físico y filósofo Ernst Mach. Mach tenía una idea algo mal definida de que dado que el movimiento es sólo una noción bien definida cuando hablamos de un objeto que se mueve en relación con otro objeto, la inercia de un objeto debe ser causada por la influencia de toda la otra materia en el universo. Einstein se refirió a esto como el principio de Mach. Los falsos inicios de Einstein en la construcción de la relatividad general se relacionaban frecuentemente con sus intentos de hacer que su teoría fuera demasiado “maquiana”. En la sección 8.3 se discute una alternativa, más maquiana, teoría de la gravedad propuesta por Brans y Dicke en 1951.