4.3: Cuatro vectores (Parte 2)

El vector de frecuencia y el desplazamiento Doppler relativista

En el espíritu de la notación índice-gimnasia, la frecuencia es al tiempo como el número de onda k =\(\frac{1}{\lambda}\) es al espacio, por lo que al tratar las ondas relativisticamente es natural conjeturar que hay _una f a de cuatro frecuencias hecha ensamblando (f, k), que se comporta como un vector Lorentz. Esto es correcto, ya que ya sabemos que\(\partial_{a}\) se transforma como un vector covariante, y para una onda escalar de la forma

\[A = A_o \exp [2\pi if_ax^a]\]

el operador derivado parcial es idéntico a la multiplicación por 2\(\pi\) f _a.

Como aplicación, considere el desplazamiento Doppler relativista de una onda de luz. Por simpicidad, limitémonos a una dimensión espacial. Para una onda de luz,\(f = k\), por lo que el vector de frecuencia en 1+1 dimensiones es simplemente (f, f). Poniendo esto a través de una transformación Lorentz, encontramos

\[f' = (1 + v) \gamma f = \sqrt{\frac{1+v}{1-v}} f,\]

donde la segunda forma muestra más claramente la forma simética de la relación relativista, de tal manera que intercambiar los roles de fuente y observador equivale a voltear el signo de v. Es decir, la versión relativista sólo depende del movimiento relativo de la fuente y del observador, mientras que el newtoniano también depende del movimiento de la fuente en relación con el medio (es decir, relativo al cuadro preferido en el que las ondas tienen la velocidad “correcta”). En mecánica newtoniana, tenemos f' = (1 + v) f para un observador en movimiento. Relativisticamente, también hay una dilatación temporal de la oscilación de la fuente, proporcionando un factor adicional de\(\gamma\).

Este análisis se extiende a 3+1 dimensiones en el problema 11.

Ejemplo 15: Experimentos de Ives-Stilwell

El desplazamiento Doppler relativista difiere del no relativista por el factor de dilatación temporal\(\gamma\), por lo que todavía hay un desplazamiento incluso cuando el movimiento relativo de la fuente y el observador es perpendicular a la dirección de propagación. A esto se le llama desplazamiento Doppler transversal. Einstein sugirió esto desde el principio como una prueba de relatividad. Sin embargo, tales experimentos son difíciles de llevar a cabo con alta precisión, ya que son sensibles a cualquier error en la alineación del ángulo de 90 grados. Dichos experimentos finalmente se realizaron, con resultados que confirmaron la relatividad, ⁷ pero las mediciones unidimensionales proporcionaron tanto las primeras pruebas del desplazamiento relativista Doppler como las más precisas hasta la fecha. La primera prueba de este tipo la realizaron Ives y Stilwell en 1938, usando el siguiente truco. La expresión relativista

\[S_{v} = \sqrt{\frac{(1 + v)}{(1 − v)}}\]

para el turno Doppler tiene la propiedad que

\[S_vS_{−v} = 1\]

que difiere del resultado no relativista de

\[(1 + v)(1 − v) = 1 − v^2.\]

Por lo tanto, se puede acelerar un ion hasta una velocidad relativista, medir tanto la frecuencia desplazada Doppler hacia delante _{f f} como la hacia atrás f _b, y calcular\(\sqrt{f_{f} f_{b}}\). Según la relatividad, esto debería ser exactamente igual a la frecuencia f _o medida en el marco de reposo del ion.

En una versión moderna particularmente exquisita de la idea Ives-Stilwell, ⁸ Saathoff et al. circularon iones Li ⁺ a v = .064 en un anillo de almacenamiento. Se utilizó una técnica de enfriador de electrones para reducir la variación de velocidad entre los iones en el haz. Dado que la identidad S _v S _−v = 1 es independiente de v, no fue necesario medir v con la misma increíble precisión que las frecuencias; solo fue necesario que fuera estable y bien definida. El ancho de línea natural fue de 7 MHz, y otros efectos experimentales la ampliaron aún más a 11 MHz. Mediante el ajuste de curva de la línea, fue posible lograr resultados buenos a unas pocas décimas de MHz. Las frecuencias resultantes, en unidades de MHz, fueron:

f _f = 582490203.44 ± .09

f _b = 512671442.9 ± 0.5

\(\sqrt{f_{f} f_{b}}\)= 546466918.6 ± 0.3

f _o = 546466918.8 ± 0.4 (del trabajo experimental previo)

El espectacular acuerdo con la teoría ha hecho de este experimento un pararrayos para los chiflados antirelatividad.

Si uno está buscando pequeñas desviaciones de las predicciones de la relatividad especial, un lugar natural para mirar es a altas velocidades. Los experimentos de IveStilwell se han realizado a velocidades tan altas como 0.84, y confirman una relatividad especial. ⁹

---

⁷ Véase, por ejemplo, Hasselkamp, Mondry y Scharmann, Zeitschrift f¨ur Physik A: Hadrones y Núcleos 289 (1979) 151.

⁸ G. Saathoff et al., “Prueba Mejorada de Dilatación en el Tiempo en la Relatividad”, Phys. Rev. Lett. 91 (2003) 190403. Una descripción del experimento disponible públicamente se da en la tesis doctoral de Saathoff, www.mpi-hd.mpg.de/ato/homes/saathoff/ diss-saathoff.pdf.

⁹ MacArthur et al., Phys. Rev. Lett. 56 (1986) 282 (1986)

2

Anteriormente, demostramos que el célebre E = mc ² sigue directamente de la forma de la transformación de Lorentz. Una derivación alternativa fue dada por Einstein en uno de sus trabajos clásicos de 1905 que exponía la teoría de la relatividad especial; el artículo es corto, y se reproduce en traducción al inglés en el Apéndice A de este libro. Habiendo sentado las bases de cuatro vectores y los cambios Doppler relativistas, podemos dar una versión aún más corta del argumento de Einstein. La discusión también se racionaliza restringiendo la discusión a 1+1 dimensiones e invocando fotones.

Supongamos que una linterna, en reposo en el marco del laboratorio, flota sin peso en el espacio exterior, y simultáneamente emite dos pulsos de luz en direcciones opuestas, cada uno con energía\(\frac{E}{2}\) y frecuencia f. Por simetría, el impulso de los pulsos se cancela, y la linterna permanece en reposo. Un observador en movimiento a velocidad v relativa al laboratorio ve las frecuencias de los haces desplazadas a f' = (1 ± v)\(\gamma\) f. El efecto sobre las energías de los haces se puede encontrar puramente clásicamente, transformando los campos eléctrico y magnético en el marco móvil, pero como atajo podemos aplicar el quantum- relación mecánica E _ph = hf para las energías de los fotones que componen los haces. El resultado es que el observador en movimiento encuentra que la energía total de los haces no es E sino (\(\frac{E}{2}\)) (1 + v)\(\gamma\) + (\(\frac{E}{2}\)) (1 − v)\(\gamma\) = E\(\gamma\).

Ambos observadores coinciden en que la linterna tuvo que agotar parte de la energía almacenada en su combustible para poder hacer los dos pulsos. Pero el observador en movimiento dice que además de esta energía E, había una energía adicional E (\(\gamma\)− 1). ¿De dónde podría haber salido esta energía? Debió provenir de la energía cinética de la linterna. La velocidad de la linterna se mantuvo constante durante todo el experimento, por lo que esta disminución de la energía cinética vista por el observador en movimiento debió provenir de una disminución en la masa inercial de la linterna, de ahí el título del artículo de Einstein, “¿La inercia de un cuerpo depende de su contenido energético?”

Para averiguar cuánta masa ha perdido la linterna, tenemos que decidir cómo podemos incluso definir la masa en este nuevo contexto. En la mecánica newtoniana, teníamos K = (\(\frac{1}{2}\)) mv ², y por el principio de correspondencia esto aún debe mantenerse en el límite de baja velocidad. Expandiendo E (\(\gamma\)− 1) en una serie de Taylor, encontramos que es igual a E (\(\frac{v^{2}}{2}\)) +., y en el límite de baja velocidad esto debe ser lo mismo que\(\Delta K = (\frac{1}{2}) \Delta mv^{2}\), así que\(\Delta\) m = E. Reinsertando factores de c para volver a unidades no relativistas, tenemos E =\(\Delta\) mc ².

Un no ejemplo: campos eléctricos y magnéticos

Es bastante fácil ver que los campos eléctrico y magnético no pueden ser las partes espaciales de dos cuatro vectores. Considere la disposición mostrada en la Figura 4.2.2 (1). Tenemos dos trenes infinitos de cargas móviles superpuestos en la misma línea, y una sola carga a lo largo de la línea. A pesar de que las cargas de línea formadas por los dos trenes se mueven en direcciones opuestas, sus corrientes no se cancelan. Una carga negativa que se mueve hacia la izquierda hace una corriente que va hacia la derecha, por lo que en el cuadro 1, la corriente total es el doble de la aportada por cualquiera de las líneas de carga.

Figura\(\PageIndex{2}\) - El magnetismo es un efecto puramente relativista.

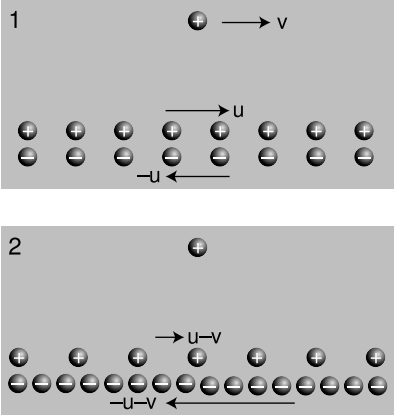
En el cuadro 1 las densidades de carga de las dos cargas de línea se cancelan, y el campo eléctrico experimentado por la carga solitaria es, por lo tanto, cero. El fotograma 2 muestra lo que veríamos si estuviéramos observando todo esto desde un marco de referencia moviéndose junto con la carga solitaria. Ambas cargas de línea están en movimiento en ambos marcos de referencia, pero en el cuadro 1, las cargas de línea se movían a velocidades iguales, por lo que sus contracciones de Lorentz fueron iguales, y sus densidades de carga cancelaron. En el cuadro 2, sin embargo, sus velocidades son desiguales. Las cargas positivas se mueven más lentamente que en el cuadro 1, por lo que en el cuadro 2 están menos contraídas. Las cargas negativas se mueven con mayor rapidez, por lo que su contracción es mayor ahora. Dado que las densidades de carga no se cancelan, hay un campo eléctrico en el marco 2, que apunta hacia el alambre, atrayendo la carga solitaria.

Parecemos tener una contradicción lógica aquí, porque un observador en el cuadro 2 predice que la carga colisionará con el cable, mientras que en el cuadro 1 parece que debería moverse con velocidad constante paralela al cable. Los experimentos muestran que la carga choca con el cable, por lo que para mantener la invarianza Lorentz del electromagnetismo, nos vemos obligados a inventar un nuevo tipo de interacción, una entre cargas móviles y otras cargas móviles, lo que provoca la aceleración en el cuadro 2. Esta es la interacción magnética, y si no la hubiéramos sabido ya, nos habríamos visto obligados a inventarla. Es decir, el magnetismo es un efecto puramente relativista. La razón por la que un efecto relativista puede ser lo suficientemente fuerte como para pegar un imán a un refrigerador es que rompe la delicada cancelación de las interacciones eléctricas extremadamente grandes entre objetos eléctricamente neutros.

Si bien el ejemplo muestra que los campos eléctrico y magnético sí se transforman cuando cambiamos de un cuadro a otro, es fácil demostrar que no se transforman como las partes espaciales de un cuatro-vector relativista. Esto se debe a que la transformación entre los marcos 1 y 2 es a lo largo del eje paralelo al cable, pero afecta a los componentes de los campos perpendiculares al cable. El campo electromagnético en realidad se transforma como un tensor de rango 2.

El potencial electromagnético de cuatro vectores

Una cantidad electromagnética que sí se transforma como un cuatro vector es el potencial. En la sección 3.7 mencioné el hecho, que puede o no ser ya familiar para usted, de que mientras que las propiedades de polarización del campo gravitacional newtoniano permiten que se describa usando un solo potencial escalar\(\phi\) o un solo campo vectorial\(\textbf{g} = − \nabla \phi\), el par de campos (E, B) necesita un par de potenciales,\(\boldsymbol{\Phi}\) y A. Es fácil ver que no\(\boldsymbol{\Phi}\) puede ser un escalar de Lorentz. La carga eléctrica q es un escalar, así que si\(\boldsymbol{\Phi}\) fuera un escalar también, entonces el producto q\(\boldsymbol{\Phi}\) sería un escalar. Pero esto es igual a la energía de la partícula cargada, que es solo el componente temporal del cuatro vector energía-impulso, y por lo tanto no un escalador Lorentz en sí mismo. Esto es una contradicción, así que no\(\boldsymbol{\Phi}\) es un escalar.

Para ver cómo\(\boldsymbol{\Phi}\) encajar en la relatividad, considere la relación mecánica cuántica no relativista q\(\boldsymbol{\Phi}\) = hf para una partícula cargada en un potencial\(\boldsymbol{\Phi}\). Dado que f es el componente temporal de un cuatro vectores en relatividad, necesitamos\(\boldsymbol{\Phi}\) ser el componente temporal de algunos cuatro vectores, Ab. Para la parte espacial de este cuatro-vector, escribamos A, para eso\(A_{b} = (\boldsymbol{\Phi}, \textbf{A})\). Podemos ver por el siguiente argumento que esta misteriosa A debe tener algo que ver con el campo magnético.

Consideremos el ejemplo de la Figura 4.2.3 desde un punto de vista cuántico-mecánico. La partícula cargada q tiene propiedades de onda, pero digamos que se puede aproximar bien en este ejemplo como siguiendo una trayectoria específica. Esto es como la aproximación de rayos a la óptica de onda. Un rayo de luz en la óptica clásica sigue el principio de Fermat, también conocido como el principio del menor tiempo, que establece que la trayectoria del rayo desde el punto A al punto B es aquella que extremiza la longitud de la trayectoria óptica (esencialmente el número de oscilaciones). La razón de esto es que la aproximación del rayo es sólo una aproximación. El rayo en realidad tiene algo de ancho, que podemos visualizar como un haz de trayectorias vecinas. Sólo si la trayectoria sigue el principio de Fermat será constructiva la interferencia entre los caminos vecinos. La longitud de ruta óptica clásica se encuentra integrando k · ds, donde k es el número de onda. Para hacer esto relativista, necesitamos usar el cuatro vector de frecuencia para formar f _{b dx ^b}, que también se puede expresar como f _b v ^b d\(\tau\) =\(\gamma\) (f − k · v) d\(\tau\). Si la carga está en reposo y no hay campos magnéticos, entonces la cantidad entre paréntesis es\(f = \frac{E}{h} = (\frac{q}{h}) \Phi\). La generalización relativista correcta es claramente f _b = (\(\frac{q}{h}\)) A _b.

Figura\(\PageIndex{3}\) - La partícula cargada sigue una trayectoria que extremiza\(\int\) f _b dx ^b en comparación con otras trayectorias cercanas. Relativisticamente, la trayectoria debe entenderse como una línea mundial en el espacio-tiempo 3+1-dimensional.

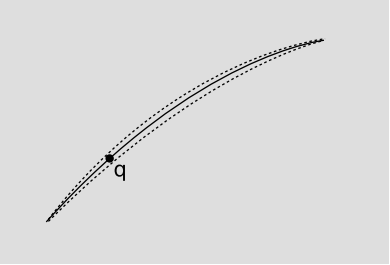
Dado que la parte espacial de Ab, A, resulta en los efectos dependientes de la velocidad, concluimos que A es una especie de potencial que se relaciona con el campo magnético, de la misma manera que el potencial\(\boldsymbol{\Phi}\) se relaciona con el campo eléctrico. A se conoce como el potencial vectorial, y la relación entre los potenciales y los campos es

\[\begin{split} \textbf{E} &= - \nabla \Phi - \frac{\partial \textbf{A}}{\partial t} \\ \textbf{B} &= \nabla \textbf{A} \ldotp \end{split}\]

Una excelente discusión sobre el potencial vectorial desde un punto de vista puramente clásico se da en las clásicas Conferencias Feynman. ¹⁰ La Figura 4.2.4 muestra un ejemplo.

Figura\(\PageIndex{4}\) - El campo magnético (arriba) y el potencial vectorial (abajo) de un solenoide. El diagrama inferior está en el plano cortando a través de la cintura del solenoide, como lo indica la línea discontinua en el diagrama superior. Para un solenoide infinito, el campo magnético es uniforme en el interior y cero en el exterior, mientras que el potencial vectorial es proporcional a r en el interior y al\(\frac{1}{r}\) exterior.

Referencias

¹⁰ Las conferencias de Feynman sobre física, Feynman, Leighton y Sands, Addison Wesley Longman, 1970