5.2: Curvatura de marea versus curvatura causada por fuentes locales

Otra complicación es la necesidad de distinguir la curvatura de las mareas de la curvatura causada por fuentes locales. La figura\(\PageIndex{1}\) muestra al cometa Shoemaker-Levy, desmenuzado en una cadena de fragmentos por las fuerzas mareales de Júpiter poco antes de su espectacular impacto con el planeta en 1994. Inmediatamente después de cada fractura, los trozos recién separados tenían una velocidad casi nula entre sí, por lo que una vez que el cometa terminó de romperse, las líneas mundiales de los fragmentos eran una gavilla de líneas casi paralelas separadas por distancias espaciales de solo 1 km. Estas geodésicas inicialmente paralelas luego divergieron, eventualmente desplegándose para abarcar millones de kilómetros.

Figura\(\PageIndex{1}\): Las fuerzas mareales interrumpen al cometa Shoemaker-Levy.

Si inicialmente las líneas paralelas pierden su paralelismo, eso es claramente una indicación de curvatura intrínseca. Lo llamamos una medida de curvatura seccional, porque la pérdida de paralelismo ocurre dentro de un plano particular, en este caso el\((t, x)\) plano representado por la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Las fuerzas mareales hacen que las líneas mundiales inicialmente paralelas de los fragmentos diverjan. El espacio-tiempo ocupado por el cometa tiene curvatura intrínseca, pero no es causado por ninguna masa local; es causado por la masa distante de Júpiter.

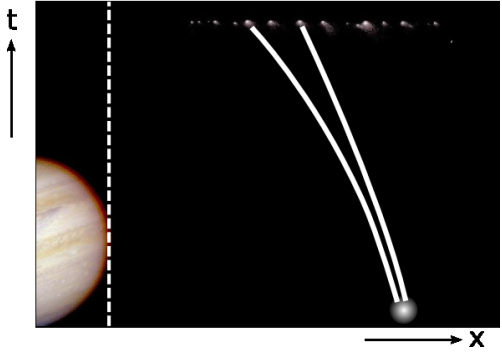
Pero esta curvatura no fue causada por una fuente local que acechaba entre los fragmentos. Fue causado por una fuente lejana: Júpiter. Por lo tanto, vemos que la mera presencia de curvatura seccional no es suficiente para demostrar la existencia de fuentes locales. Incluso el signo de la curvatura seccional no es una indicación confiable. Si bien este ejemplo mostró una divergencia de geodésicas inicialmente paralelas, referidas como curvatura negativa, también es posible que las fuerzas mareales ejercidas por masas distantes creen una curvatura positiva. Por ejemplo, las mareas oceánicas en la tierra oscilan tanto por encima como por debajo del nivel medio del mar, Figura Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): El campo gravitacional de la luna provoca que los océanos de la Tierra se distorsionen en elipsoide. El signo de la curvatura seccional es negativo en el plano x − t, pero positivo en el plano y − t.

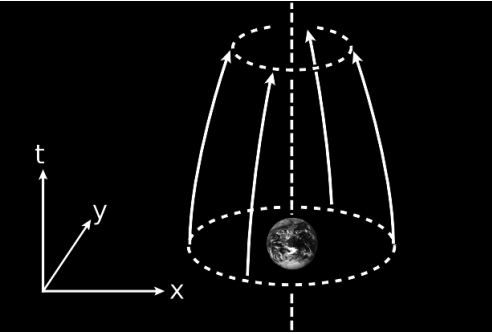
Como ejemplo que realmente indicaría la presencia de una fuente local, podríamos liberar una nube de masas de prueba en reposo en una concha esférica alrededor de la tierra, y permitirles caer, Figura\(\PageIndex{4}\). Tendríamos entonces una curvatura seccional positiva e igual en los\(t − z\) planos\(t − x\)\(t − y\),, y. Tal observación no puede deberse a una masa distante. Demuestra una contracción general del volumen de una gavilla inicialmente paralela de geodésicas, que nunca puede ser inducida por las fuerzas mareales. Los océanos de la tierra, por ejemplo, no cambian su volumen total debido a las mareas, y esto sería cierto incluso si los océanos fueran un gas más que un fluido incompresible. Es una propiedad única de\(\frac{1}{r^{2}}\) fuerzas como la gravedad que conserven el volumen de esta manera; esto es esencialmente una reafirmación de la ley de Gauss en un vacío.

Figura\(\PageIndex{4}\): Una nube de masas de prueba se libera en reposo en una concha esférica alrededor de la tierra, que se muestra aquí como un círculo porque se omite el eje z. El volumen del proyectil se contrae a lo largo del tiempo, lo que demuestra que la curvatura local del espacio-tiempo es generada por una fuente local —la tierra— en lugar de alguna distante.