6.2: La métrica Schwarzschild (Parte 1)

Ahora nos fijamos el objetivo de encontrar la métrica que describe el espacio-tiempo estático fuera de un cuerpo de masa esféricamente simétrico, no giratorio, m. Este problema fue resuelto por primera vez por Karl Schwarzschild en 1915. ³ Un subproducto de encontrar esta métrica será la capacidad de calcular exactamente el efecto geodésico, pero tendrá consecuencias de mayor alcance, incluida la existencia de agujeros negros. El problema que estamos resolviendo es similar a calcular la solución esféricamente simétrica a la ley de Gauss en un vacío. La solución al problema eléctrico es de la forma\(\dfrac{\hat{\textbf{r}}}{r^{2}}\), con una constante arbitraria de proporcionalidad que resulta ser proporcional a la carga que crea el campo. Una gran diferencia, sin embargo, es que mientras que la ley de Gauss es lineal, la ecuación

\[R_{ab} = 0\]

es altamente no lineal, por lo que la solución no puede simplemente escalarse hacia arriba y hacia abajo en proporción a\(m\).

La razón de esta no linealidad es fundamental para la relatividad general. Por ejemplo, cuando la tierra se condensó fuera de la nebulosa solar primordial, se produjeron grandes cantidades de calor, y esta energía se irradió gradualmente hacia el espacio exterior, disminuyendo la masa total de la tierra. Si pretendemos, como en la Figura\(\PageIndex{1}\), que este proceso implicó la fusión de sólo dos cuerpos, cada uno con masa m, entonces el resultado neto fue esencialmente tomar las masas separadas m y m en reposo, y acercarlas para formar masas cercanas m y m, nuevamente en reposo. La cantidad de energía irradiada fue proporcional a m ², por lo que la masa gravitacional del sistema combinado se ha reducido de\(2m\) a\(2m−(. . .)m^2\), donde. es aproximadamente\(\dfrac{G}{c^{2} r}\). Existe una dependencia no lineal del campo gravitacional sobre las masas.

Figura\(\PageIndex{1}\): Las ecuaciones de campo de la relatividad general son no lineales.

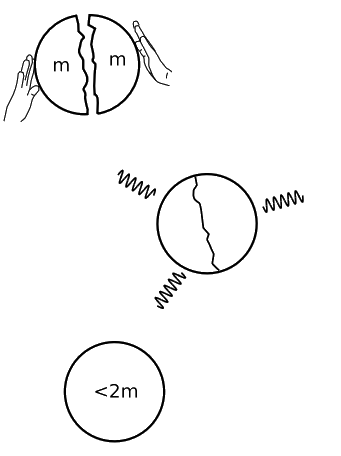
Ejercicio\(\PageIndex{1}\)

La firma de una métrica se define como la lista de signos positivos y negativos que ocurren cuando se diagonaliza. ⁴ El principio de equivalencia requiere que la firma sea + − −− (o − + ++, dependiendo de la elección de las convenciones de signo). Verifique que cualquier métrica constante (incluida una métrica con la firma “incorrecta”, por ejemplo, 2+2 dimensiones en lugar de 3+1) sea una solución a la ecuación de campo de Einstein en vacío.

---

⁴ Véase la sección 6.3 para un uso diferente pero estrechamente relacionado del mismo término.

El principio de correspondencia nos dice que nuestro resultado debe tener un límite newtoniano, pero las únicas variables involucradas son m y r, por lo que este límite debe ser aquel en el que\(\dfrac{r}{m}\) sea grande. ¿Grande en comparación con qué? No hay nada más disponible con lo que comparar, por lo que sólo puede ser grande comparado con alguna expresión compuesta por las constantes unitless G y c. Ya hemos elegido unidades de tal manera que\(c = 1\), y ahora vamos a establecer\(G = 1\) también. La masa y la distancia son ahora comparables, siendo el factor de conversión\(\dfrac{G}{c^{2}} = 7 \times 10^{^−28} \,m/kg\), o aproximadamente una milla por masa solar. Dado que el radio de la tierra es miles de veces más de una milla, y su masa cientos de miles de veces menor que la del sol,\(\dfrac{r}{m}\) es muy grande, y la aproximación newtoniana es lo suficientemente buena para todas las aplicaciones menos precisas, como la red GPS o el experimento Gravity Probe B.

El caso de masa cero

Primero demostremos la solución trivial con espacio-tiempo plano. En coordenadas esféricas, tenemos

\[ds^{2} = dt^{2} - dr^{2} - r^{2} \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2} \ldotp\]

Los símbolos de Christoffel que no se desvanecen (ignorando los swaps de los índices inferiores) son:

\[\begin{split} \Gamma^{\theta}_{r \theta} &= \dfrac{1}{r} \\ \Gamma^{\phi}_{r \phi} &= \dfrac{1}{r} \\ \Gamma^{r}_{\theta \theta} &= -r \\ \Gamma^{r}_{\phi \phi} &= -r \sin^{2} \theta \\ \Gamma^{\theta}_{\phi \phi} &= \sin \theta \cos \theta \\ \Gamma^{\phi}_{\theta \phi} &= \cot \theta \end{split}\]

Ejercicio\(\PageIndex{2}\)

Si hubiéramos estado usando la métrica (− + ++) en lugar de (+ − −−), ¿cuál habría sido el efecto en los símbolos de Christoffel? ¿Y si hubiéramos expresado la métrica en diferentes unidades, reescalando todas las coordenadas por un factor k?

Uso del tensor c

De hecho, cuando calculé los símbolos de Christoffel arriba a mano, me equivoqué a uno de ellos, y me perdí calcular uno al otro porque pensé que era cero. Sólo encontré mi error comparando con un resultado en un libro de texto. El cómputo del tensor Riemann es un desastre aún mayor. Claramente es una buena idea recurrir a un sistema de álgebra computacional aquí. Cadabra, que se discutió anteriormente, está diseñado específicamente para cálculos independientes de coordenadas, por lo que aquí no nos va a ayudar. Una buena opción libre y de código abierto es ctensor, que es uno de los paquetes estándar distribuidos junto con el sistema de álgebra computacional Maxima, introducido en la sección 2.5.

El siguiente programa Maxima calcula los símbolos de Christoffel encontrados anteriormente.

La línea 1 carga el paquete ctensor. La línea 2 establece los nombres de las coordenadas. La línea 3 define la g _ab, con 1g que significa “la versión de g con índices más bajos”. La línea 7 le dice a Maxima que haga algún trabajo de configuración con g _ab, incluido el cálculo de la matriz inversa g ^ab, que se almacena en ug. La línea 8 dice para calcular los símbolos de Christoffel. La notación mcs se refiere al tensor\(\Gamma'^{a}_{bc}\) con los índices intercambiados un poco en comparación con la convención\(\Gamma^{a}_{bc}\) seguida en este libro. En un sistema Linux, colocamos el programa en un archivo flat.mac y lo ejecutamos usando el comando maxima -b flat.mac. La parte relevante de la salida es:

Añadiendo el comando ricci (true); al final del programa da como resultado la salida ESTE ESPACIOTIEMPO ESTÁ VACÍO Y/O PLANO, lo que nos ahorra horas de tedioso cómputo. Se calcula el tensor ric (que aquí resulta ser cero), y se imprimen todos sus elementos distintos de cero. Hay un comando similar riemann (true); para computar el riem rensor de Riemann. Esto se almacena para que riem [i, j, k, l] sea lo que llamaríamos R ^l _ikj. Tenga en cuenta que l se mueve hasta el final, y j y k también se intercambian.

Unidades Geométricas

Si la masa que crea el campo gravitacional no es cero, entonces tenemos que decidir en qué unidades medirlo. Ya ha resultado muy conveniente adoptar unidades con\(c = 1\), y ahora también estableceremos la constante gravitacional\(G = 1\). Anteriormente, con solo c ajustado a 1, las unidades de tiempo y longitud eran las mismas, [T] = [L], y así lo fueron las unidades de masa y energía, [M] = [E]. Con G = 1, todas estas se convierten en las mismas unidades:

\[ [T] = [L] = [M] = [E].\]

Ejercicio\(\PageIndex{3}\)

Verifica esta afirmación combinando la ley de la gravedad de Newton con la segunda ley del movimiento de Newton.

El sistema resultante se conoce como geometrizado, porque unidades como la masa que antes habían pertenecido a la provincia de la mecánica ahora se miden usando las mismas unidades que usaríamos para hacer geometría.

Un límite de R grande

Ahora pensemos en cómo abordar el problema real de encontrar la métrica no plana. Aunque la relatividad general nos permite elegir las coordenadas que nos gusten, la simetría esférica del problema sugiere usar coordenadas que explotan esa simetría. El espacio plano coordina\(\theta\) y\(\phi\) puede definirse de la misma manera, y tienen la misma interpretación. Por ejemplo, si dejamos caer una partícula de prueba hacia la masa desde algún punto en el espacio, su línea mundial tendrá constante\(\theta\) y\(\phi\). La coordenada r es un poco diferente. En el espacio-tiempo curvo, la circunferencia de un círculo no es igual a 2\(\pi\) veces la distancia desde el centro al círculo; de hecho, la discrepancia entre estos dos es esencialmente la definición de la curvatura de Ricci. Esto nos da la opción de dos formas lógicas para definir r. La definiremos como la circunferencia dividida por 2\(\pi\), lo que tiene la ventaja de que los dos últimos términos de la métrica son los mismos que en el espacio plano:

\[−r^2d\theta^{2} −r^2 \sin^2 \theta\, d \phi^{2}.\]

Como estamos buscando soluciones estáticas, ninguno de los elementos de la métrica puede depender de t. Además, la solución va a ser simétrica bajo t → −t, y\(\theta \rightarrow − \theta\), por lo tanto\(\phi \rightarrow − \phi\), no podemos tener ningún elemento fuera de la diagonal. ⁵ El resultado es que hemos reducido la métrica a algo de la forma

\[ds^{2} = h(r) dt^{2} - k(r) dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2},\]

donde tanto h como k se acercan a 1 para r →\(\infty\), donde el espacio-tiempo es plano.

⁵ Para más información sobre la simetría de inversión de tiempo, ver más adelante.

Para orientación sobre cómo construir h y k, consideremos la aceleración de una partícula de prueba at\(r \gg m\), que sabemos que es\(− \dfrac{m}{r^{2}}\), ya que ahí se aplica la física no relativista. Tenemos

\[\nabla_{t} v^{r} = \partial_{t} v^{r} + \Gamma^{r}_{tc} v^{c} \ldotp\]

Un observador que cae libremente junto con la partícula observa que su aceleración es cero, y un tensor que es cero en un sistema de coordenadas es cero en todos los demás. Dado que la derivada covariante es un tensor, concluimos que\(\nabla_{t} v^{r}\) = 0 en todos los sistemas de coordenadas, incluyendo el sistema (t, r,.) que estamos usando. Si la partícula se libera del reposo, entonces inicialmente su velocidad de cuatro vectores es (1, 0, 0, 0), por lo que encontramos que su aceleración en las coordenadas (t, r) es\(− \Gamma^{r}_{tt} = − \dfrac{1}{2} g^{rr} \partial_{r} g_{tt} = − \dfrac{1}{2} \dfrac{h'}{k}\). Estableciendo esto igual a\(− \dfrac{m}{r^{2}}\), encontramos\(\dfrac{h'}{k} = \dfrac{2m}{r^{2}}\) para r >> m. Desde k ≈ 1 para r grande, tenemos

\[h' \approx \dfrac{2m}{r^{2}} \; for \; r >> m \ldotp\]

La interpretación de este cálculo es la siguiente. Afirmamos el principio de equivalencia, mediante el cual se puede decir que la aceleración de una partícula de caída libre es cero. Después de algunos cálculos, encontramos que la velocidad a la que fluye el tiempo (codificado en h) no es constante. Es diferente para observadores a diferentes alturas en un pozo de potencial gravitacional. Pero esto es algo que ya habíamos deducido, sin la gimnasia índice, en el ejemplo 7.

Integrando, encontramos que para grandes r, h = 1 −\(\dfrac{2m}{r}\).

La solución completa

Una solución de la serie

Hemos aprendido algunas cosas interesantes, pero todavía tenemos una ecuación diferencial no lineal extremadamente desagradable que resolver. Una forma de atacar una ecuación diferencial, cuando no tienes idea de cómo proceder, es probar una solución en serie. Tenemos un pequeño parámetro\(\dfrac{m}{r}\) para expandirnos, así que intentemos escribir h y k como series del formulario

\[h = \sum_{n = 0}^{\infty} a_{k} \left(\dfrac{m}{r}\right)^{n}\]

\[k = \sum_{n = 0}^{\infty} b_{k} \left(\dfrac{m}{r}\right)^{n}\]

Ya conocemos a ₀, a ₁ y b ₀. Tratemos de encontrar b ₁. En el siguiente código Maxima omito el factor de m en h ₁ por conveniencia. En otras palabras, estamos buscando la solución para m = 1.

No voy a reproducir toda la salida del tensor Ricci, que es voluminoso. Queremos que sus cuatro componentes que no se desvanezcan lo más rápido posible para grandes valores de r, así que decidí jugar con R _tt, que parecía tan simple como cualquiera de ellos. Parece variar como r ⁻⁴ para r grande, así que evaluemos\(\lim_{r \rightarrow \infty} (r^{4} R_{tt})\):

El resultado es\(\dfrac{(b_{1}−2)}{2}\), así que pongamos b ₁ = 2. La solución aproximada que hemos encontrado hasta ahora (reinsertando las m),

\[ds^{2} \approx \left(1 - \dfrac{2m}{r}\right) dt^{2} - \left(1 + \dfrac{2m}{r}\right) dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2},\]

fue derivado por primera vez por Einstein en 1915, y lo utilizó para resolver el problema de la corrección relativista no kepleriana a la órbita de Mercurio, que fue una de las primeras pruebas empíricas de relatividad general.

Continuando de esta manera, los resultados son los siguientes:

$$\ begin {split} a_ {0} &= 1\\ a_ {1} &= -2\\ a_ {2} &= 0\\ a_ {3} &= 0\ end {split} $$

$$\ begin {split} b_ {0} &= 1\\ b_ {1} &= 2\\ b_ {2} &= 4\\ b_ {2} &= 8\ end {split} $$

La solución de forma cerrada

La solución es inesperadamente simple, y se puede poner en forma cerrada. El resultado aproximado que encontramos para h fue de hecho exacto. Para k tenemos una serie geométrica\(\dfrac{1}{(1 − \dfrac{2}{r})}\), y cuando reinsertamos el factor de m de la única manera que hace que las unidades funcionen, obtenemos\(\dfrac{1}{(1 − \dfrac{2m}{r})}\). El resultado para la métrica es

\[ds^{2} = \left(1 - \dfrac{2m}{r}\right) dt^{2} - \left(\dfrac{1}{1 - \dfrac{2m}{r}}\right) dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2} \ldotp\]

A esto se le llama la métrica Schwarzschild. Un cálculo rápido en Maxima demuestra que es una solución exacta para todos los r, es decir, el tensor Ricci desaparece por todas partes, incluso a r < 2m, que está fuera del radio de convergencia de la serie geométrica.

Simetría de inversión de tiempo

La métrica Schwarzschild es invariante bajo inversión de tiempo, ya que el tiempo se produce sólo en la forma de\(dt^2\), que permanece igual bajo dt → − dt. Esta es la misma simetría de inversión de tiempo que ocurre en la gravedad newtoniana, donde el campo es descrito por la aceleración gravitacional g, y las aceleraciones son invariantes de inversión en el tiempo.

Fundamentalmente, este es un ejemplo de independencia coordinada de la relatividad general. Las leyes de la física proporcionadas por la relatividad general, como la ecuación de campo vacío, son invariantes bajo cualquier transformación de coordenadas suave, y t → −t es una transformación de coordenadas de este tipo, por lo que la relatividad general tiene simetría de inversión de tiempo. Dado que la métrica de Schwarzschild se encontró imponiendo condiciones de límite de tiempo-reversalsimétricas en una ecuación diferencial tiempo-reversal-simétrica, es una solución igualmente válida cuando la invertimos en el tiempo. Además, se espera que la métrica sea invariable bajo la inversión temporal, a menos que se produzca una ruptura espontánea de simetría (ver sección 8.2).

Esto sugiere que planteamos la pregunta más fundamental de qué simetrías globales tiene la relatividad general. ¿Tiene simetría bajo inversión de paridad, por ejemplo? ¿O podemos tomar alguna solución como el espacio-tiempo Schwarzschild y transformarlo en un marco de referencia en el que la fuente del campo se mueve uniformemente en cierta dirección? Debido a que la relatividad general es localmente equivalente a la relatividad especial, sabemos que estas simetrías son localmente válidas. Pero puede que ni siquiera sea posible definir las simetrías globales correspondientes. Por ejemplo, hay algunos espacio-tiempos en los que ni siquiera es posible definir una coordenada temporal global. En tal espacio-tiempo, que se describe como no orientable al tiempo, no existe ningún campo vectorial suave que esté en todas partes parecido al tiempo, por lo que no es posible definir conos de luz pasados versus futuros en todos los puntos del espacio sin que se produzca un cambio discontinuo en la definición en alguna parte. Esto es similar a la forma en que una tira de Möbius no permite definir globalmente una orientación de su superficie (una dirección “hacia arriba” vista por una hormiga).

Supongamos que nuestro espacio-tiempo es orientable al tiempo, y somos capaces de definir coordenadas (p, q, r, s) de tal manera que p sea siempre la coordenada temporal. Debido a que q → −q es una transformación de coordenadas suave, se nos garantiza que nuestro espacio-tiempo sigue siendo una solución válida de las ecuaciones de campo bajo este cambio. Pero eso no quiere decir que lo que hemos encontrado es una simetría bajo inversión de paridad en un plano. Nuestra coordenada q no es necesariamente interpretable como distancia a lo largo de un “eje q” particular. Tales ejes ni siquiera existen globalmente en la relatividad general. Una coordenada ni siquiera tiene que tener unidades de tiempo o distancia; podría ser un ángulo, por ejemplo, o podría no tener ningún significado geométrico en absoluto. De igual manera, podríamos hacer una transformación q → q' = q + kp. Si pensamos en q como medir la posición espacial y el p tiempo, entonces esto parece una transformación galileana, siendo k la velocidad. La solución a las ecuaciones de campo obtenidas después de realizar esta transformación sigue siendo una solución válida, pero eso no significa que la relatividad tenga simetría galilea en lugar de simetría de Lorentz. No hay manera sensata de definir una transformación galileana actuando sobre todo un espacio-tiempo, porque cuando hablamos de una transformación galileana asumimos la existencia de cosas como ejes de coordenadas globales, que ni siquiera existen en la relatividad general.

Referencias

³ “Sobre el campo gravitacional de una masa puntual según la teoría de Einstein”, Sitzungsberichte der Koniglich Preussischen Akademie der Wissenschaften 1 (1916) 189. Una traducción al inglés está disponible en http://arxiv.org/abs/physics/9905030v1.