9.2: Radiación gravitacional (Parte 1)

Evidencia empírica

La primera evidencia empírica fuerte de ondas gravitacionales llegó en 1982. El sistema Hulse-Taylor (sección 6.2) contiene dos estrellas de neutrones que orbitan alrededor de su centro de masa común, y se observa que el período de la órbita disminuye gradualmente con el tiempo (Figura 9.2.1). Esto se interpreta como evidencia de que las estrellas están perdiendo energía a causa de la radiación de las ondas gravitacionales. ⁴ Como veremos más adelante, la tasa de pérdida de energía está en excelente acuerdo con las predicciones de la relatividad general.

Figura\(\PageIndex{1}\) - El movimiento orbital del púlsar de Hulse-Taylor está perdiendo energía gradualmente debido a la emisión de ondas gravitacionales. La disminución lineal del periodo se integra en esta parcela, resultando en una parábola. De Weisberg y Taylor, http://arxiv.org/abs/astro-ph/0211217.

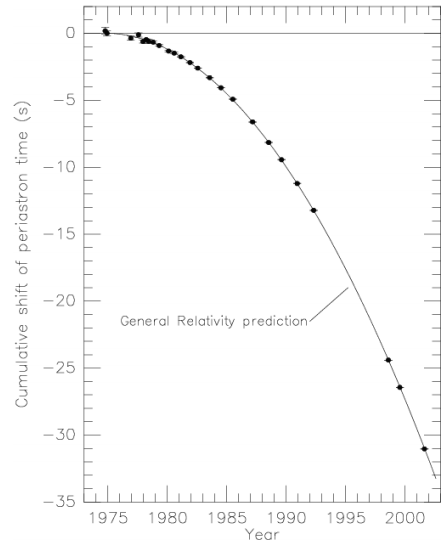
Una evidencia aún más dramática, aunque menos clara, es la observación ⁵ de Komossa, Zhou y Lu de un agujero negro supermasivo que parece estar retrocediendo de su galaxia madre a una velocidad de 2650 km/s (proyectada a lo largo de la línea de visión). Interpretan esto como evidencia para el siguiente escenario. En el universo temprano, las galaxias se forman con agujeros negros supermasivos en sus centros. Cuando dos galaxias de este tipo chocan, los agujeros negros pueden fusionarse. La fusión es un proceso violento en el que se emiten intensas ondas gravitacionales, y estas ondas llevan una gran cantidad de impulso, haciendo que los agujeros negros retrocedan a una velocidad mayor que la velocidad de escape de la galaxia fusionada.

Si bien la pérdida de energía de sistemas como el binario Hulse-Taylor proporciona una fuerte evidencia de que las ondas gravitacionales existen y transportan energía, los físicos y astrónomos aún querían detectarlas directamente, y serios intentos de diseñar y construir tales sistemas comenzaron alrededor de 1962. El diseño que finalmente logró el éxito utilizó interferómetros que detectan oscilaciones en la longitud de sus propios brazos. El primer evento de onda gravitacional fue detectado, por este método, en 2016, por la colaboración Advanced LIGO. ⁶ Se cree que el suceso fue el resultado de la colisión de dos agujeros negros.

Figura\(\PageIndex{2}\) - La forma de onda gravitacional observada en 2016 por Advanced Ligo.

En 2017, un evento interpretado como la colisión de dos estrellas de neutrones fue detectado tanto por radiación gravitacional como electromagnética, verificando con alta precisión que las ondas gravitacionales se propagan a c.

Aunque la anterior colisión de agujeros negros de 2016 no comparó directamente la propagación de la luz y la gravedad, proporcionó un tipo diferente de verificación sobre la propagación de las ondas gravitacionales en c. La forma de onda detectada en este evento fue un “chirp” que se deslizó en frecuencia a medida que los agujeros negros giraban en espiral hacia el uno al otro y aceleró. Dado que la onda estuvo en tránsito por más de mil millones de años, y la forma de onda duró una fracción de segundo, se deduce que las ondas gravitacionales dentro de este rango de frecuencia viajan casi a la misma velocidad, es decir, hay un límite superior muy estrecho en la dispersión de las ondas gravitacionales.

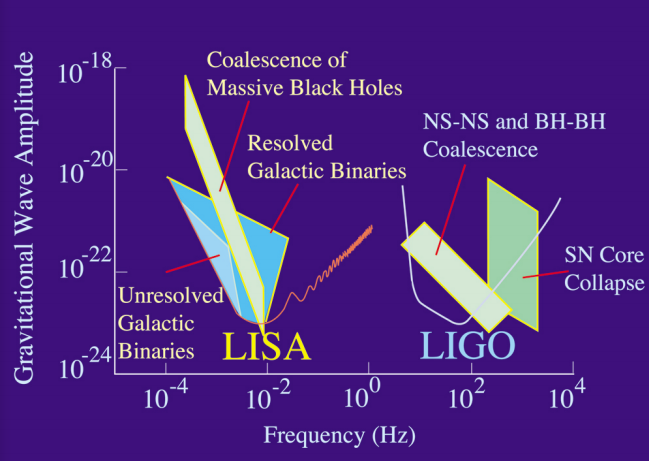
Un sistema complementario basado en el espacio, LISA, ha sido propuesto para su lanzamiento en 2020, pero su financiamiento es incierto. Los dos dispositivos operarían en rangos de frecuencia complementarios (Figura 9.2.3). Un punto de venta de LISA es que si se lanza, hay una serie de fuentes en el cielo, con propiedades conocidas, que se sabe que están fácilmente dentro de su rango de sensibilidad. ⁷ Un excelente candidato es HM Cancri, un par de enanas blancas con un periodo orbital de 5.4 minutos, más corto que el de cualquier otra estrella binaria conocida. ⁸

Figura\(\PageIndex{3}\) - Sensibilidades pronosticadas de LISA y LIGO a ondas gravitacionales de diversas frecuencias.

Contenido Energético

Incluso sin realizar los cálculos para un sistema como el binario de Hulse-Taylor, es fácil demostrar que si existen tales ondas, deben ser capaces de llevar energía. Considere dos masas iguales en órbitas altamente elípticas alrededor de su centro de masa común, Figura 9.2.4. El movimiento es casi unidimensional. A medida que las masas retroceden unas de otras, sienten una versión retardada de la fuerza gravitacional originada en una época en la que estaban más juntas y la fuerza era más fuerte. El resultado es que en el límite casi newtoniano, pierden más energía cinética y gravitacional de la que habrían perdido en la teoría puramente newtoniana. Ahora vuelven hacia adentro en sus órbitas. A medida que se acercan entre sí, la fuerza retardada en el tiempo es anómalamente débil, por lo que ganan menos energía mecánica de la esperada. El resultado es que con cada ciclo se pierde energía mecánica. Esperamos que esta energía sea transportada por las ondas, de la misma manera que las ondas de radio transportan la energía perdida por una antena transmisora. ⁹

Figura\(\PageIndex{4}\) - A medida que los dos planetas retroceden uno del otro, cada uno siente la atracción gravitacional que el otro ejerció en su posición anterior, retrasada por el tiempo que tardan los efectos gravitacionales en propagarse en c. En el tiempo t, el planeta de la derecha experimenta la desaceleración más fuerte correspondiente a la posición más cercana del planeta izquierdo en el momento anterior t', no su posición actual en t. La energía mecánica no se conserva, y las órbitas se desintegrarán

Nota

Hay que tener cuidado con este tipo de argumentos. En particular, se pueden obtener resultados correctos incorrectos al intentar generalizar este argumento unidimensional al movimiento en más de una dimensión, porque la interacción seminewtoniana efectiva no es solo una versión retardada en el tiempo de la ley de Newton; también incluye fuerzas dependientes de la velocidad. Es fácil ver por qué tal dependencia de la velocidad debe ocurrir en el caso más simple del electromagnetismo. Supongamos que los cargos A y B no están en reposo relativos entre sí. En el cuadro de B, el campo eléctrico de A debe provenir de la dirección de la posición que un observador comoving con B extrapolaría linealmente de la última posición y velocidad conocidas de A, según lo determinado por el cálculo de la velocidad de la luz. Esto se desprende de la invarianza de Lorentz, ya que esta es la dirección que verá un observador comoving con A. Una discusión completa la da Carlip, arxiv.org/abs/gr-qc/9909087v2.

Estas ondas no sólo pueden eliminar energía mecánica de un sistema, también pueden depositar energía en un detector, como lo demuestra el no matemático “argumento de cuentas pegajosas” (Figura 9.2.5), que fue originado por Feynman en 1957 y posteriormente popularizado por Bondi.

Figura\(\PageIndex{5}\) - El argumento del grano pegajoso para la realidad de las ondas gravitacionales. A medida que pasa una onda gravitacional con la polarización apropiada, el cordón vibra hacia adelante y hacia atrás sobre la varilla. La fricción crea calor. Esto demuestra que las ondas gravitacionales transportan energía y, por lo tanto, son fenómenos reales y observables.

Ahora estrictamente hablando, solo hemos demostrado que las ondas gravitacionales pueden extraer o donar energía mecánica, pero no que las ondas mismas transmitan esta energía. La distinción no es la que normalmente se nos ocurre, ya que estamos capacitados para creer que la energía siempre se conserva. Pero sabemos que, por razones fundamentales, la relatividad general no tiene leyes de conservación globales que se apliquen a todos los espacio-tiempos (sección 4.5). Quizás la energía perdida por el sistema Hulse-Taylor simplemente se ha ido, para nunca reaparecer, y la energía impartida a la cuenta pegajosa simplemente se genera de la nada. Por otro lado, la relatividad general sí cuenta con leyes de conservación globales para ciertas clases específicas de espacio-tiempo, incluyendo, por ejemplo, una masa-energía escalar conservada en el caso de un espacio-tiempo estacionario (sección 7.1). Los espacio-tiempos que contienen ondas gravitacionales no son estacionarios, pero quizás haya algo similar que podamos hacer en algún caso especial apropiado.

Supongamos que queremos una expresión para la energía de una onda gravitacional en términos de su amplitud. Esto parece que debería ser sencillo. Tenemos tales expresiones en otras teorías clásicas de campo. En electromagnetismo, tenemos densidades de energía + (\(\frac{1}{8 \pi k}\)) | E | ² y + (\(\frac{1}{2 \mu_{o}}\)) | B | ² asociadas a los campos eléctrico y magnético. En la gravedad newtoniana, podemos asignar una densidad de energía − (\(\frac{1}{8 \pi G}\)) | g | ² al campo gravitacional g; el signo menos indica que cuando las masas se desvanecen unas sobre otras, producen un campo mayor y se libera energía.

En general la relatividad, sin embargo, el principio de equivalencia nos dice que para cualquier campo gravitacional medido por un observador, podemos encontrar otro observador, uno que cae libremente, que dice que el campo local es cero. De ello se deduce que no podemos asociar una energía con la curvatura de una región particular del espacio-tiempo de ninguna manera exacta. Lo mejor que podemos hacer es encontrar expresiones que den la densidad de energía (1) en el límite de campos débiles, y (2) cuando se promedian sobre una región del espacio que es grande en comparación con la longitud de onda. Estas expresiones no son únicas. Hay varias formas de escribirlas en términos de la métrica y sus derivadas, y todas dan el mismo resultado en el límite apropiado. El lector que esté interesado en ver el tema desarrollado a detalle es remitido a las Notas de la Conferencia de Carroll sobre Relatividad General, arxiv.org/abs/gr-qc/? 9712019. Aunque este tipo de cosas son técnicamente desordenadas, podemos lograr bastante simplemente sabiendo que tales resultados sí existen, y que aunque no son únicos en general, están singularmente bien definidos en ciertos casos. Específicamente, cuando se quiere hablar de ondas gravitacionales, suele ser posible asumir un espacio-tiempo asintóticamente plano. En un espacio-tiempo asintóticamente plano, existe una masa-energía escalar, llamada masa ADM, que se conserva. En este sentido restringido, se nos asegura que los libros se equilibran, y que la emisión y absorción de ondas gravitacionales realmente significa la transmisión de una cantidad fija de energía.

Propiedades esperadas

Para ver qué propiedades debemos esperar de la radiación gravitacional, primero consideremos el razonamiento que llevó a la construcción de los tensores Ricci y Einstein. Si un cierto volumen de espacio se llena con partículas de prueba, entonces los tensores Ricci y Einstein miden la tendencia de este volumen a “acelerar”; es decir,\(− \frac{d^{2} V}{dt^{2}}\) es una medida de la atracción de cualquier masa que se encuentre dentro del volumen. Una masa distante, sin embargo, ejercerá únicamente fuerzas mareales, que distorsionan una región sin cambiar su volumen. Esto sugiere que a medida que una onda gravitacional pasa por una determinada región del espacio, debe distorsionar la forma de una región determinada, sin cambiar su volumen.

Cuando se discutió por primera vez la idea de las ondas gravitacionales, hubo cierto escepticismo sobre si representaban un efecto que era observable, incluso en principio. La duda más ingenua es del mismo sabor que la discutida en la sección 8.2 sobre la observabilidad de la expansión del universo: si todo se distorsiona, entonces ¿no se distorsionan también nuestras varitas métricas, haciendo imposible medir el efecto? La respuesta es la misma que antes en la sección 8.2; los sistemas que están ligados gravitacional o electromagnéticamente no tienen sus escalas distorsionadas en una cantidad igual al cambio en los elementos de la métrica.

Figura\(\PageIndex{6}\) - A medida que la onda gravitacional se propaga en la dirección z, la métrica oscila en las direcciones x e y, conservando el volumen.

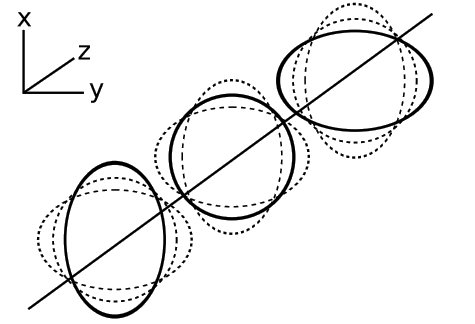
Una razón menos ingenua para ser escépticos sobre las ondas gravitacionales es que solo porque una métrica parece oscilatoria, eso no significa que su comportamiento oscilatorio sea observable. Considera el siguiente ejemplo.

\[ds^{2} = dt^{2} - \left(1 + \dfrac{1}{10} \sin x \right) dx^{2} - dy^{2} - dz^{2}\]

Los símbolos de Christoffel dependen de derivados de la forma\(\partial_{a} g_{bc}\), así que aquí es el único símbolo de Christoffel que no se desvanece\(\Gamma^{x}_{xx}\). Entonces es sencillo comprobar que el tensor Riemann

\[R^{a}_{bcd} = \partial_{c} \Gamma^{a}_{db} − \partial_{d} \Gamma^{a}_{cb} + \Gamma^{a}_{ce} \Gamma^{e}_{db} − \Gamma^{a}_{de} \Gamma^{e}_{cb}\]

desaparece por simetría. Por lo tanto, esta métrica debe ser realmente solo una métrica plano-espacio-tiempo que ha sido sometida a un tonto cambio de coordenadas.

Ejercicio\(\PageIndex{1}\)

Autocomprobación: R desaparece, pero\(\Gamma\) no. ¿Hay alguna razón para prestar más atención a uno u otro?

Para evitar que la curvatura se desvanezca, parece que necesitamos una métrica en la que la oscilación no esté restringida a una sola variable.

Por ejemplo, la métrica

\[ds^{2} = dt^{2} - \left(1 + \frac{1}{10} \sin y \right) dx^{2} - dy^{2} - dz^{2}\]

tiene curvatura que no se desvanece. En otras palabras, parece que deberíamos estar buscando ondas transversales más que longitudinales. ¹⁰ Por otro lado, esta métrica no puede ser una solución a las ecuaciones de campo de vacío, ya que no conserva el volumen. También se detiene, mientras que esperamos que las soluciones a las ecuaciones de campo se propaguen a la velocidad de la luz, al menos para amplitudes pequeñas. Estas conclusiones son autoconsistentes, porque la polarización de una onda solo puede restringirse si se propaga en c (ver sección 4.2).

Nota

0Un tratamiento más cuidadoso muestra que las ondas longitudinales siempre pueden interpretarse como ondas coordinadas físicamente inobservables, en el límite de grandes distancias desde la fuente. Por otro lado, es claro que tal prohibición contra las ondas longitudinales podría aplicarse universalmente, ya que tal restricción solo puede ser invariante de Lorentz si la onda se propaga en c (ver sección 4.2), mientras que las ondas de alta amplitud no necesitan propagarse en c. Ondas longitudinales cercanas a la fuente se denominan soluciones Tipo III en un esquema de clasificación debido a Petrov. Las ondas transversales, que son lo que realmente podríamos observar en experimentos prácticos, son de tipo N.

Basándonos en lo que hemos descubierto, lo siguiente parece una métrica que podría tener una probabilidad de combate de representar una onda gravitacional real:

\[ds^{2} = dt^{1} - (1 + A \sin (z - t)) dx^{2} - \frac{dy^{2}}{1 + A \sin (z - t)} - dz^{2}\]

Es transversal, se propaga en c (= 1), y el hecho de que g _xx sea el recíproco de g _yy la hace conservadora de volumen. El siguiente programa Maxima calcula su tensor Einstein:

Para un componente representativo del tensor Einstein, encontramos

\[G_{tt} = \frac{A^{2} \cos^{2} (z - t)}{2 + 4 A \sin (z - t) + 2A^{2} \sin^{2} (z - t)}\]

Para valores pequeños de A, tenemos |G _tt |\(\lesssim \frac{A^{2}}{2}\). Las ecuaciones de campo de vacío requieren G _tt = 0, por lo que esta no es una solución exacta. Pero todos los componentes de G, no sólo G _tt, son del orden A ², por lo que esta es una solución aproximada a las ecuaciones.

También es sencillo verificar que la propagación a aproximadamente c era una característica necesaria. Por ejemplo, si reemplazamos los factores de sin (z −t) en la métrica con sin (z −2t), obtenemos un G _xx que es de unidad de orden, no de orden ^A2.

Para probar que las ondas gravitacionales son un efecto observable, nos gustaría poder mostrar una métrica que (1) sea una solución exacta de las ecuaciones de campo de vacío; (2) no sea simplemente una onda de coordenadas; y (3) lleve impulso y energía. Ya en 1936, Einstein y Rosen publicaron un artículo que afirmaba que las ondas gravitacionales eran un artefacto matemático, y en realidad no existían. ¹¹

Referencias

⁴ Escaleras, “Probando Relatividad General con Pulsar Timing”, relativity.livingreviews.org/... es/lrr-2003-5/

⁵ http://arxiv.org/abs/0804.4585

⁶ https://dcc.ligo.org/LIGO-P150914/public

⁷ G. nelemanos, “El primer plano de la onda gravitacional galáctica”, arxiv.org/abs/0901.1778v1

⁸ Roelofs et al., “Evidencia espectroscópica para un periodo orbital de 5.4 minutos en HM Cancri”, arxiv.org/abs/1003.0658v1

¹¹ Parte de la historia está relacionada en http://en.Wikipedia.org/wiki/Sticky_bead_argument.