9.3: Radiación gravitacional (Parte 2)

En esta sección estudiamos varios ejemplos de soluciones exactas a las ecuaciones de campo. Se puede demostrar fácilmente que cada uno de estos no es una mera onda de coordenadas, ya que en cada caso el tensor Riemann tiene elementos distintos de cero.

Ejemplo 1: Una solución exacta

Ya hemos visto, por ejemplo, en la derivación de la métrica Schwarzschild en la sección 6.2, que una vez que tenemos una solución aproximada a las ecuaciones de la relatividad general, es posible que podamos encontrar una solución en serie. Históricamente este enfoque solo se utilizó como último recurso, porque la falta de computadoras hacía que los cálculos fueran demasiado complejos para manejarlos, y la tendencia era buscar trucos que hicieran posible una solución de forma cerrada. Pero hoy el método de la serie tiene la ventaja de que cualquier mero mortal puede tener alguna esperanza razonable de éxito con él —y no hay nada más aburrido (o desmoralizador) que aprender laboriosamente el truco especial de otra persona que solo funciona para un problema específico. En este ejemplo, veremos que tal enfoque se acerca tentadoramente a proporcionar una solución exacta de onda plana oscilatoria a las ecuaciones de campo.

Nuestra mejor solución hasta ahora era de la forma

\[ds^{2} = dt^{2} - (1 + f) dx^{2} - \frac{dy^{2}}{1 + f} - dz^{2}, \tag{9.2.6}\]

donde f = Asin (z − t). Esto no parece probable que sea una solución exacta para grandes amplitudes, ya que las coordenadas x e y se tratan asimétricamente. En el caso extremo de |A| ≥ 1, habría singularidades en g _yy, pero no en g _xx. Claramente la métrica tendrá que tener algún tipo de dependencia no lineal de f, pero simplemente no hemos encontrado la dependencia no lineal correcta. Supongamos que intentamos algo de esta forma:

\[ds^{2} = dt^{2} - (1 + f + cf^{2}) dx^{2} - (1 - f + df^{2}) dy^{2} - dz^{2} \tag{9.2.7}\]

Esto conserva aproximadamente el volumen, ya que (1+f +.) (1−f +.) es igual a la unidad, hasta términos de orden f ². El siguiente programa prueba este formulario.

En la línea 3, la motivación para usar lo exponencial complejo más que una onda sinusoidal en f es la habitual de obtener expresiones más simples; como veremos, esto termina causando problemas. En las líneas 5 y 6 no se han definido los símbolos c y d, y no se han declarado como dependientes de otras variables, por lo que Maxima los trata como constantes desconocidas. El resultado es G _tt ∼ (4d + 4c − 3) A ² para A pequeña, por lo que podemos hacer desaparecer el término A ² mediante una elección apropiada de d y c. Para la simetría, elegimos c = d =\(\frac{3}{8}\). Con estos valores de las constantes, el resultado para G _tt es del orden A ⁴. Esta técnica se puede extender a órdenes de aproximación cada vez más altos, dando como resultado una solución de serie exacta a las ecuaciones de campo.

Desafortunadamente, toda la historia termina siendo demasiado buena para ser verdad. La métrica resultante tiene elementos de valor complejo. Si la relatividad general fuera una teoría de campo lineal, entonces podríamos aplicar la técnica habitual de formar combinaciones lineales de expresiones de la forma e ^+i... y e ^−i... , para dar un resultado real. Pero las ecuaciones de campo de la relatividad general son no lineales, por lo que la combinación lineal resultante ya no es una solución. Lo mejor que podemos hacer es hacer una solución exponencial real no oscilatoria (problema 2).

Ejemplo 2: Una solución exacta, oscilatoria, no monocromática

Asumir una métrica de la forma

\[ds^{2} = dt^{2} - p(z - t)^{2} dx^{2} - q(z - t)^{2} dy^{2} - dz^{2}, \ldots \tag{9.2.8}\]

donde p y q son funciones arbitrarias. Tal métrica representaría claramente algún tipo de onda plana polarizada transversalmente que viaja a la velocidad c (= 1) en la dirección z. El siguiente código Maxima calcula su tensor Einstein.

El resultado es proporcional a\(\frac{\ddot{q}}{q} + \frac{\ddot{p}}{p}\), por lo que cualquier función p y q que satisfaga la ecuación diferencial\(\frac{\ddot{q}}{q} + \frac{\ddot{p}}{p}\) = 0 dará como resultado una solución a las ecuaciones de campo. Estableciendo p (u) = 1 + Acos u, por ejemplo, encontramos que q es oscilatorio, pero con un periodo superior a 2\(\pi\) (problema 3).

Ejemplo 3: Una onda exacta, plana y monocromática

Cualquier métrica de la forma

\[ds^{2} = (1 - h) dt^{2} - dx^{2} - dy^{2} - (1 + h) dz^{2} + 2hdzdt, \tag{9.2.9}\]

donde h = f (z − t) xy, y f es cualquier función, es una solución exacta de las ecuaciones de campo (problema 4).

Debido a que h es proporcional a xy, esto no parece a primera vista ser una onda plana uniforme. Sin embargo, se puede verificar que todos los componentes del tensor Riemann dependen únicamente de z − t, no de x o y, por lo tanto, no existe una propiedad medible de esta métrica que varíe con x e y.

Tasa de Radiación

¿Cómo podemos encontrar la tasa de radiación gravitacional de un sistema como el púlsar de Hulse-Taylor?

Procedamos por analogía. La fuente más simple de ondas sonoras es algo así como el cono de un altavoz estéreo. Dado que las ondas sonoras típicas tienen longitudes de onda medidas en metros, todo el altavoz es generalmente pequeño en comparación con la longitud de onda. El cono del altavoz es una superficie de desplazamiento oscilante\(x = x__o \sin \omega t\). Idealizando tal fuente a una superficie esférica radialmente pulsante, tenemos un monopolo oscilante que irradia ondas sonoras de manera uniforme en todas las direcciones. Para encontrar la potencia radiada, observamos que la velocidad de la fuente-superficie es proporcional a x _o\(\omega\), por lo que la energía cinética del aire inmediatamente en contacto con ella es proporcional a\(\omega^{2}x^2_o\). La potencia irradiada es, por lo tanto, proporcional a\(\omega^{2} x^2_o\).

Figura\(\PageIndex{7}\): La potencia emitida por una fuente multipolar de orden\(m\) es proporcional a\(\omega^{2(m+1)}\), cuando el tamaño de la fuente es pequeño en comparación con la longitud de onda. La razón principal de la dependencia ω es que a bajas frecuencias, la longitud de onda es larga, por lo que el número de longitudes de onda viajadas a un punto particular en el espacio es casi el mismo desde cualquier punto de la fuente; por lo tanto, obtenemos una fuerte cancelación.

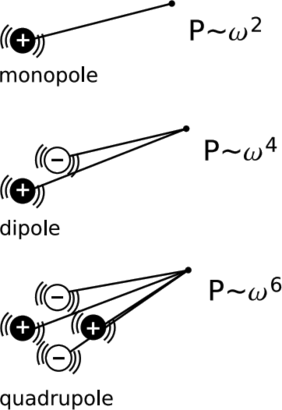
En el electromagnetismo, la conservación de la carga prohíbe la existencia de un monopolo eléctrico oscilante. La fuente de radiación más simple es, por lo tanto, un dipolo eléctrico oscilante D = D _o sin\(\omega\) t. Si el tamaño físico del dipolo es pequeño en comparación con una longitud de onda de la radiación, entonces la radiación es un proceso ineficiente; en cualquier punto del espacio, solo hay una pequeña diferencia en la longitud de la trayectoria entre las porciones positiva y negativa del dipolo, por lo que tiende a haber una fuerte cancelación de sus contribuciones, las cuales fueron emitidas con fases opuestas. El resultado es que el potencial electromagnético de cuatro vectores de la onda (Sección 4.2) es proporcional a D _o\(\omega\), los campos a D _o\(\omega^{2}\), y la potencia radiada a D ² _o\(\omega^{4}\). El factor de se\(\omega^{4}\) puede descomponer en (\(\omega^{2}\)) (\(\omega^{2}\)), donde el primer factor de\(\omega^{2}\) ocurre por razones similares a las que explican el\(\omega^{2}\) factor para la radiación monopolo del sonido, mientras que el segundo\(\omega^{2}\) surge porque cuanto menor es ω, cuanto más larga es la longitud de onda, y mayor es la ineficiencia en la radiación causada por el pequeño tamaño de la fuente en comparación con la longitud de onda.

Ejemplo 4: am radio

La radio AM comercial utiliza longitudes de onda de varios cientos de metros, por lo que las antenas dipolo AM suelen ser órdenes de magnitud más cortas que una longitud de onda. Esto provoca una atenuación severa tanto en la transmisión como en la recepción. (Hay teoremas llamados teoremas de reciprocidad que relacionan la eficiencia de la transmisión con la eficiencia de la recepción.) Por lo tanto, los receptores necesitan usar una gran cantidad de amplificación. Esto no causa problemas, porque las fuentes ambientales de ruido de RF son atenuadas por la antena corta tan severamente como la señal.

Como nuestro universo no parece tener partículas con masa negativa, no podemos formar un dipolo gravitacional poniendo masas positivas y negativas en extremos opuestos de un palo — y además, tal palo no girará libremente alrededor de su centro, ¡porque su centro de masa no se encuentra en su centro! En un sistema más realista, como el púlsar de Hulse-Taylor, tenemos dos masas desiguales orbitando alrededor de su centro de masa común. Por conservación del momento, el momento dipolar de masa de tal sistema es constante, por lo que no podemos tener un dipolo de masa oscilante. La fuente más simple de radiación gravitacional es, por lo tanto, un cuadrupolo de masa oscilante, Q = Q _o sin\(\omega\) t Al igual que en el caso del dipolo eléctrico oscilante, la radiación se suprime si, como suele ser el caso, la fuente es pequeña en comparación con la longitud de onda. La supresión es aún más fuerte en el caso de un cuadrupolo, y el resultado es que la potencia radiada es proporcional a Q ² _o\(\omega^{6}\).

Este resultado tiene la interesante propiedad de ser invariante bajo una reescalación de coordenadas. En unidades geométricas, la masa, la distancia y el tiempo tienen todas las mismas unidades, de modo que Q ² _o tiene unidades de (longitud ³) ² mientras que\(\omega^{6}\) tiene unidades de (longitud) ⁻⁶. Esto es exactamente lo que se requiere, porque en unidades geométricas, la potencia es sin unidades, energía/tiempo = longitud/longitud = 1.

También podemos vincular la\(\omega^{6}\) dependencia a nuestro argumento anterior a favor de la disipación de energía por ondas gravitacionales. El argumento fue que los cuerpos gravitatorios están sujetos a fuerzas gravitacionales retardadas en el tiempo, con el resultado de que las órbitas tienden a decaer. Este argumento sólo funciona si las fuerzas varían en el tiempo; si las fuerzas son constantes a lo largo del tiempo, entonces el retardo de tiempo no tiene efecto. Por ejemplo, en el límite semi-newtoniano el campo de una hoja de masa es independiente de la distancia de la lámina. (El análogo eléctrico de este hecho se prueba fácilmente usando la ley de Gauss.) Si dos láminas paralelas caen una hacia la otra, entonces ninguna está sujeta a una fuerza variable en el tiempo, por lo que no habrá radiación. En general, esperamos que no haya radiación gravitacional de una partícula a menos que la tercera derivada de su posición d3 x/ dt 3 sea distinta de cero. (Lo mismo es cierto para la radiación eléctrica cuadrupolo.) En el caso especial donde la posición oscila sinusoidalmente, la regla de la cadena nos dice que tomar la tercera derivada equivale a sacar a relucir un factor de\(\omega^{3}\). Dado que la amplitud de las ondas gravitacionales es proporcional a\(\frac{d^{3} x}{dt^{3}}\), su energía varía como (\(\frac{d^{3} x}{dt^{3}}\)) ², o\(\omega^{6}\).

El patrón general que hemos observado es que para la radiación multipolar de orden m (0=monopolo, 1=dipolo, 2=cuadrupolo), la potencia radiada depende de\(\omega^{2(m+1)}\). Dado que la radiación gravitacional siempre debe tener m = 2 o superior, tenemos la\(\omega^{6}\) dependencia muy pronunciada de la potencia en la frecuencia. Esto demuestra que si queremos ver una fuerte radiación gravitacional, necesitamos mirar sistemas que están oscilando extremadamente rápido. Para un sistema binario con masas desiguales de orden m, con órbitas que tienen radios de orden r, tenemos Q _o ∼ mr ². Las leyes de Newton dan\(\omega\) ∼ m ^1/2 r ^−3/2, que es esencialmente la ley de períodos de Kepler. El resultado es que la potencia radiada debe depender de (\(\frac{m}{r}\)) ⁵. Reinsertando las constantes adecuadas para dar una ecuación que permita el cálculo práctico en unidades SI, tenemos

\[P = k \frac{G^{4}}{c^{5}} \left(\dfrac{m}{r}\right)^{5}, \tag{9.2.10}\]

donde k es una constante sin unidad de unidad de orden.

Para el púlsar de Hulse-Taylor, ¹² tenemos m ∼ 3 × 10 ³⁰ kg (aproximadamente una masa solar y media) y r ∼ 10 ⁹ m. el púlsar binario está hecho a pedido de nuestros propósitos, ya que\(\frac{m}{r}\) es extremadamente grande comparado con lo que se ve en casi cualquier otro sistema astronómico. La estimación resultante para la potencia es de aproximadamente 10 ²⁴ vatios. Se observa que el periodo del púlsar se alarga constantemente a una velocidad de\(\alpha\) = 2.418 × 10 ⁻¹² segundos por segundo. Para comparar esto con nuestra cruda estimación teórica, tomamos la energía newtoniana del sistema\(\frac{Gm^{2}}{r}\) y multiplicamos por\(\omega \alpha\), dando 10 ²⁵ W, que comprueba dentro de un orden de magnitud. Un cálculo general-relativista completo reproduce el valor observado de\(\alpha\) a dentro de las barras de error de 0.1% de los datos.

Referencias

¹² http://arxiv.org/abs/astro-ph/0407149