3.4: Observaciones sobre la Teoría Ergódica

Template:MathJaxArovas

Definición de Ergodicidad

Un sistema mecánico evoluciona de acuerdo con las ecuaciones de movimiento de Hamilton. Hemos visto como tal sistema es recurrente en el sentido de Poincar é.

Hay un nivel más allá de la recurrencia llamado ergodicidad. En un sistema ergódico, los promedios de tiempo a lo largo de intervalos\([0,T]\)\(T\to\infty\) pueden ser reemplazados por promedios de espacio de fase. El promedio de tiempo de una función\(f(\Bvphi)\) se define como

\[\big\langle f(\Bvphi)\big\rangle\ns_t=\lim_{T\to\infty}{1\over T}\!\int\limits_0^T\!\!dt\,f\big(\Bvphi(t)\big)\ .\]

Para un sistema hamiltoniano, el promedio del espacio de fase de la misma función se define por

\[\big\langle f(\Bvphi)\big\rangle\ns_S=\int\!\!d\mu\,f(\Bvphi)\,\delta\big(E-H(\Bvphi)\big) \bigg/ \!\int\!\!d\mu\,\delta\big(E-H(\Bvphi)\big) \ ,\]

dónde\(H(\Bvphi)=H(\Bq,\Bp)\) está el hamiltoniano, y dónde\(\delta(x)\) está la\(\delta\) función Dirac. Por lo tanto,

\[{ ergodicity}\quad\Longleftrightarrow\quad \big\langle f(\Bvphi)\big\rangle\ns_t=\big\langle f(\Bvphi)\big\rangle\ns_S\ ,\]

para todas las funciones suaves\(f(\Bvphi)\) para las que\(\big\langle f(\Bvphi)\big\rangle\ns_S\) existe y es finita. Tenga en cuenta que no promediamos sobre todo el espacio de fase. Más bien, promediamos solo sobre una hipersuperficie a lo largo de la cual\(H(\Bvphi)=E\) se fija, sobre uno de los conjuntos de niveles de la función hamiltoniana. Esto se debe a que la dinámica preserva la energía. Ergodicidad significa que casi todos los puntos\(\Bvphi\), tras la evolución hamiltoniana, se moverán de tal manera que eventualmente pasen por cada vecindario finito en la superficie energética, y pasarán el mismo tiempo en regiones iguales del espacio de fase.

\(\xhi\ns_\CR(\Bvphi)\)Sea la función característica de una región\(\CR\):

\[\xhi\ns_\CR(\Bvphi)=\begin{cases} 1 & { if}\ \Bvphi\in \CR\\ 0 & { otherwise,}\end{cases}\]

donde\(H(\Bvphi)=E\) para todos\(\Bvphi\in\CR\). Entonces

\[\big\langle \xhi\ns_\CR(\Bvphi)\big\rangle\ns_t=\lim_{T\to\infty} \bigg({\hbox{ time spent in}\ \CR\over T}\bigg)\ .\]

Si el sistema es ergódico, entonces

\[\big\langle \xhi\ns_\CR(\Bvphi)\big\rangle\ns_t=P(\CR)= { D\ns_\CR(E)\over D(E)}\ ,\]

donde\(P(\CR)\) está la probabilidad a priori de encontrar\(\Bvphi\in\CR\), basada únicamente en los volúmenes relativos de\(\CR\) y de todo el espacio de fase. Este último viene dado por

\[D(E)=\int\!\!d\mu\>\delta\big(E-H(\Bvphi)\big)\ ,\]

llamada densidad de estados, es la superficie del espacio de fase en energía\(E\), y

\[D\ns_\CR(E)=\int\limits_\CR\!\!d\mu\,\delta\big(E-H(\Bvphi)\big)\ .\]

es la densidad de estados para el subconjunto de espacio de fase\(\CR\). Tenga en cuenta que

\[\begin{aligned} D(E)&\equiv\int\!\!d\mu\>\delta\big(E-H(\Bvphi)\big) =\int\limits\ns_{\CS\ns_E} \!\!\!{dS\over |\bnabla\! H|}\\ &={d\over dE}\int\!\!d\mu\>\RTheta\big(E-H(\Bvphi)\big)={d\ROmega(E)\over dE}\ .\end{aligned}\]

Aquí,\(dS\) es el elemento superficial diferencial,\(\CS\ns_E\) es la\(H\) hipersuperficie constante\(H(\Bvphi)=E\), y\(\ROmega(E)\) es el volumen de espacio de fase sobre el cual\(H(\Bvphi)<E\). Tenga en cuenta también que podemos escribir

\[d\mu=dE\,d\Sigma\ns_E\ ,\]

donde

\[d\Sigma\ns_E={dS\over |\bnabla\! H|}\bigg|\nd_{H(\Bvphi)=E}\]

es el elemento de superficie invariante.

El conjunto microcanónico

La distribución,

\[\vrh\ns_E(\Bvphi)={\delta\big(E-H(\Bvphi)\big) \over D(E)}={\delta\big(E-H(\Bvphi)\big) \over \int\!d\mu\, \delta\big(E-H(\Bvphi)\big) }\ ,\]

define el conjunto microcanónico (\(\mu\)CE) de Gibbs.

También podríamos escribir

\[\big\langle f(\Bvphi)\big\rangle\ns_S={1\over D(E)}\int\limits_{\CS\ns_E}\! d\Sigma\ns_E\,f(\Bvphi)\ ,\]

integrándose sobre la hipersuperficie\(\CS\ns_E\) en lugar de todo el espacio de fase.

Figura La velocidad espacial de fase\(\PageIndex{1}\): constante en un ángulo irracional sobre un espacio de fase toroidal es ergódica, pero no se mezcla. Un círculo sigue siendo un círculo, y una mancha sigue siendo una mancha.

Ergodicidad y mezcla

El hecho de que un sistema sea ergódico, no significa necesariamente que\(\vrh(\vphi,t)\to\vrh^{ eq}(\Bvphi)\), para considerar el siguiente movimiento en el espacio toroidal\(\big(\Bvphi=(q,p)\,\big|\, 0\le q< 1 \ ,\ 0\le p < 1\big\}\), donde identificamos bordes opuestos, impongamos condiciones de contorno periódicas. También tomamos\(q\) y\(p\) ser adimensionales, por simplicidad de notación. Que la dinámica sea dada por

\[{\dot q}=1 \qquad,\qquad {\dot p}=\alpha\ .\]

La solución es

\[q(t)=q\ns_0+t\qquad,\qquad p(t)=p\ns_0+\alpha t\ ,\]

por lo tanto, las curvas de fase están dadas por

\[p=p\ns_0+\alpha(q-q\ns_0)\ .\]

Consideremos ahora el promedio de alguna función\(f(q,p)\). Podemos escribir\(f(q,p)\) en términos de su transformada de Fourier,

\[f(q,p)=\sum_{m,n}{\hat f}\ns_{mn}\,e^{2\pi i(mq+np)}\ .\]

Tenemos, entonces,

\[f\big(q(t),p(t)\big)=\sum_{m,n}{\hat f}\ns_{mn}\,e^{2\pi i(mq\ns_0+np\ns_0)}\,e^{2\pi i(m+\alpha n)t}\ .\]

Ahora podemos realizar el promedio de tiempo de\(f\):

\[\begin{split} \big\langle f(q,p)\big\rangle\ns_t&={\hat f}\ns_{00}+\lim_{T\to\infty}\ {1\over T}\ {\sum_{m,n}}'\,{\Hf}\ns_{mn}\, e^{2\pi i(mq\ns_0+np\ns_0)}\,{e^{2\pi i(m+\alpha n)T}-1\over 2\pi i (m+\alpha n)}\\ &={\hat f}\ns_{00} \quad\hbox{ if $\alpha$ irrational.} \end{split}\]

Claramente,

\[\big\langle f(q,p)\big\rangle\ns_S=\int\limits_0^1\!\!dq\!\int\limits_0^1\!\!dp\,f(q,p)={\hat f}\ns_{00}=\big\langle f(q,p)\big\rangle\ns_t\ ,\]

por lo que el sistema es ergódico.

Figura\(\PageIndex{2}\): La transformación del panadero es un estiramiento, corte y reempaque sucesivos.

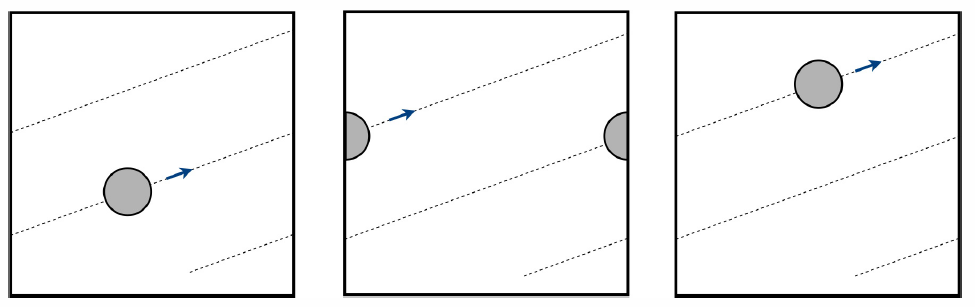
La situación se representa en la Figura\(\PageIndex{1}\). Si empezamos con la función característica de un disco,

\[\vrh(q,p,t=0)=\RTheta\big(a^2-(q-q\ns_0)^2-(p-p\ns_0)^2\big)\ ,\]

entonces sigue siendo la función característica de un disco:

\[\vrh(q,p,t)=\RTheta\big(a^2-(q-q\ns_0-t)^2-(p-p\ns_0-\alpha t)^2\big)\ ,\]

Para un ejemplo de una transición a la ergodicidad en un modelo dinámico sencillo hamiltoniano, ver § 9.

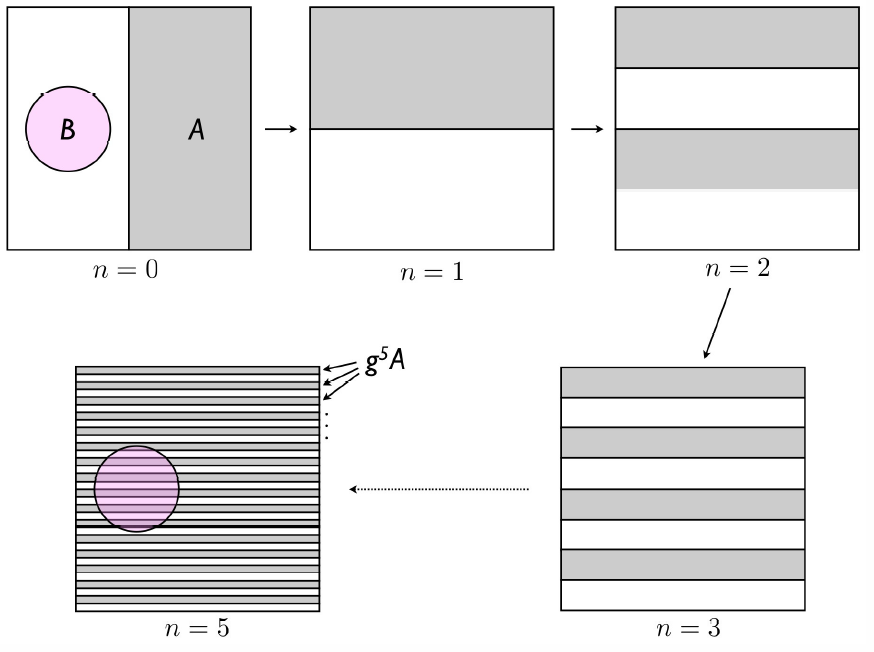
Una condición más fuerte que uno podría imponer es la siguiente. Dejar\(A\) y\(B\) ser subconjuntos de\(\CS\ns_E\). Definir la medida

\[\nu(A)=\int\!\!d\Sigma\ns_E\>\xhi\ns_A(\Bvphi)\bigg/\!\!\int\!d\Sigma\ns_E={D\ns_A(E)\over D(E)}\ ,\]

donde\(\xhi\ns_A(\Bvphi)\) está la función característica de\(A\). La medida de un conjunto\(A\) es la fracción de la superficie de energía\(\CS\ns_E\) cubierta por\(A\). Esto significa\(\nu(\CS\ns_E)=1\), ya que\(\CS\ns_E\) es todo el espacio de fase en energía\(E\). Ahora vamos a\(g\) ser un mapa que preserva el volumen sobre el espacio de fase. Dados dos conjuntos medibles\(A\) y\(B\), decimos que un sistema se está mezclando si

\[{ mixing} \qquad\Longleftrightarrow\qquad \lim_{n\to\infty}\nu\Big(g^n \! A\cap B\Big)= \nu(A)\,\nu(B)\ .\]

En otras palabras, la fracción de\(B\) cubierto por la\(n^{\ssr{th}}\) iteración de\(A\),\(g^n \!A\), es, como\(n\to\infty\), simplemente la fracción de\(\CS\ns_E\) cubierto por\(A\). El mapa iterado\(g^n\) distorsiona la región\(A\) tan severamente que finalmente se extiende 'uniformemente' sobre toda la hipersuperficie de energía. Por supuesto, por 'uniformemente' nos referimos a 'con respecto a cualquier escala de longitud finita', porque en las escalas más pequeñas, la densidad del espacio de fase sigue siendo localmente constante a medida que uno evoluciona con la dinámica.

Figura\(\PageIndex{3}\): La transformación del panadero iterada multiplicada. El conjunto A cubre la mitad del espacio de fase y su área se conserva bajo el mapa. Inicialmente, la fracción de B cubierta por A es cero. Después de muchas iteraciones, la fracción de B cubierta por\(g^n\!\RA\) enfoques\(\half\).

Mezclar significa que

\[\begin{split} \big\langle f(\Bvphi)\big\rangle&=\int\!\!d\mu\,\vrh(\Bvphi,t)\,f(\Bvphi)\\ &\bmapright{t\to\infty} \>\int\!\!d\mu\,f(\Bvphi)\,\delta\big(E-H(\Bvphi)\big)\bigg/\!\!\int\!\!d\mu\,\delta\big(E-H(\Bvphi)\big)\bvph\\ &\equiv\Tra \!\Big[f(\Bvphi)\,\delta\big(E-H(\Bvphi)\big)\Big]\Big/\Tra \!\Big[\delta\big(E-H(\Bvphi)\big)\Big]\ . \end{split}\]

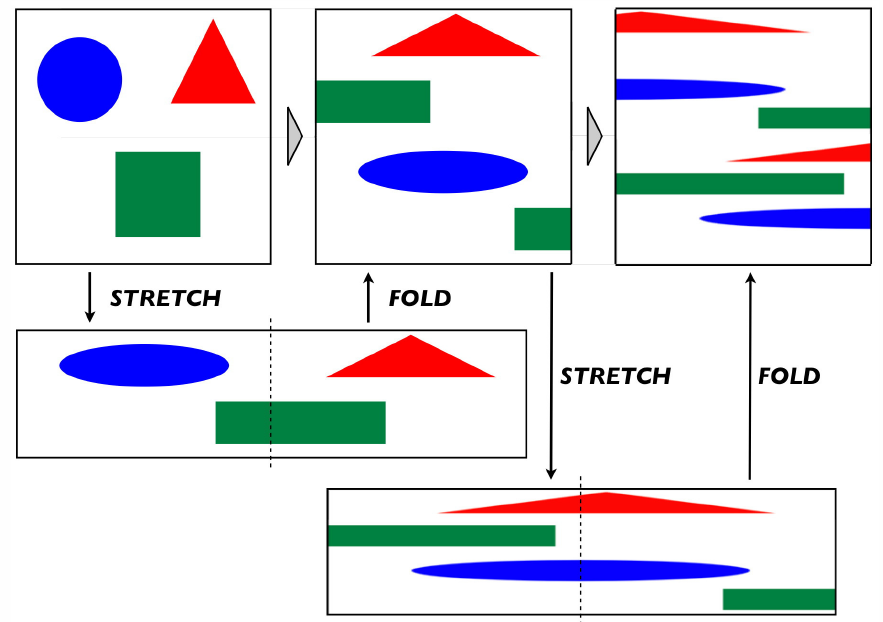
Físicamente, podemos imaginar regiones del espacio de fase que se estiran y pliegan sucesivamente. Durante el proceso de estiramiento, el volumen se conserva, por lo que las sucesivas operaciones de estiramiento y plegado mapean el espacio de fase sobre sí mismo.

Un ejemplo de un sistema de mezcla es la transformación del panadero, representada en la Figura\(\PageIndex{2}\). El mapa del panadero está definido por

\[g(q,p)=\begin{cases} \big(2q\,,\,{1\over 2}p\big) & { if}\quad 0\le q < {1\over 2} \\ &\\ \big(2q-1 \,,\, {1\over 2}p+{1\over 2}\big) & { if}\quad {1\over 2} \le q < 1\ . \end{cases}\]

Tenga en cuenta que\(g\) es invertible y conserva el volumen. La transformación del panadero consiste en un tramo inicial en el que\(q\) se expande en un factor de dos y\(p\) se contrae por un factor de dos, lo que conserva el volumen total. Luego, el sistema se mapea de nuevo en el área original cortando y replegando, lo que podemos llamar un 'plegado'. La transformación inversa se logra estirando primero en la dirección vertical (\(p\)) y machacando en la dirección horizontal (\(q\)), seguido de un corte y reagrupamiento. De manera explícita,

\[g^{-1}(q,p)=\begin{cases} \big({1\over 2}q\,,\,2p\big) & { if}\quad 0\le p < {1\over 2} \\ &\\ \big({1\over 2}q + {1\over 2} \,,\, 2p-1 \big) & { if}\quad {1\over 2} \le p < 1\ . \end{cases}\]

Figura\(\PageIndex{4}\): El mapa del gato Arnold aplicado a una imagen de\(150\times 150\) píxeles. Después de 300 iteraciones, la imagen se repite. (Fuente: Wikipedia)

Otro ejemplo de un sistema de mezcla es el 'cat map' de Arnold ⁹

\[g(q,p)=\big(\,[q+p]\, , \, [q+2p]\,\big)\ ,\]

donde\([x]\) denota la parte fraccionaria de\(x\). Uno puede escribir esto en forma de matriz como

\[\begin{pmatrix} q' \\ p' \end{pmatrix} = \stackrel{M}{\overbrace{\begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix}}} \begin{pmatrix} q \\ p \end{pmatrix} \ { mod}\ \MZ^2\ .\]

La matriz\(M\) es muy especial porque tiene entradas enteras y su determinante es\({ det}\,M=1\). Esto significa que la inversa también tiene entradas enteras. La transformación inversa es entonces

\[\begin{pmatrix} q \\ p \end{pmatrix} = \stackrel{M^{-1}}{\overbrace{\begin{pmatrix} 2 & -1 \\ -1 & 1 \end{pmatrix}}} \begin{pmatrix} q' \\ p' \end{pmatrix} \ { mod}\ \MZ^2\ .\]

Ahora por algo genial. Supongamos que nuestra imagen consiste en un conjunto de puntos discretos ubicados en\((n\ns_1/k\,,\,n\ns_2/k)\), donde\(k\in \MZ\) se fija el denominador, y dónde\(n\ns_1\) y\(n\ns_2\) rango sobre el conjunto\(\{1,\ldots,k\}\). Claramente\(g\) y su inversa preservan este conjunto, ya que las entradas de\(M\) y\(M^{-1}\) son enteros. Si hay dos posibilidades para cada píxel (decir apagado y encendido, o blanco y negro), entonces hay\(2^{(k^2)}\) posibles imágenes, y el mapa del gato nos mapeará invertiblemente de una imagen a otra. Por lo tanto debe exhibir Poincar é recurrencia! Este fenómeno se demuestra vívidamente en la Figura\(\PageIndex{4}\), que muestra una imagen en\(k=150\) píxeles (cuadrados) de un gato sometido al mapa de gatos iterado. La imagen se estira y dobla con cada aplicación sucesiva del mapa de gatos, pero después de 300 iteraciones ¡se restaura la imagen! ¿Cómo puede ser esto si el mapa del gato se está mezclando? El punto es que sólo el conjunto discreto de puntos\((n\ns_1/k\,,\,n\ns_2/k)\) es periódico. Los puntos con diferentes denominadores exhibirán una periodicidad diferente, y los puntos con coordenadas irracionales en general nunca volverán a sus condiciones iniciales exactas, aunque la recurrencia dice que se acercarán arbitrariamente, dadas suficientes iteraciones. La transformación del panadero también es diferente en este sentido, ya que el denominador de la\(p\) coordenada se duplica en cada iteración sucesiva.

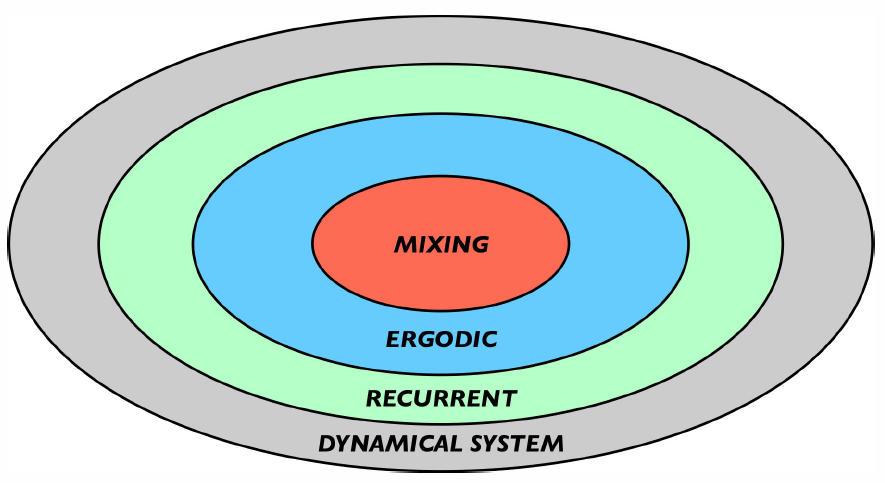
El alumno debe ahora contemplar la jerarquía de sistemas dinámicos representados en la Figura\(\PageIndex{5}\), entendiendo los rasgos característicos de cada refinamiento sucesivo ¹⁰.

Figura\(\PageIndex{5}\): La jerarquía de los sistemas dinámicos.