1.4: Principio de superposición

Se encuentra empíricamente que mientras las amplitudes de las ondas en la mayoría de los medios sean pequeñas, dos ondas en la misma ubicación física no interactúan entre sí. Así, por ejemplo, dos ondas que se mueven en sentido contrario simplemente pasan una a través de la otra sin que se cambien sus formas o amplitudes. Cuando se coloca, el desplazamiento total de las olas es solo la suma de los desplazamientos de las olas individuales. A esto se le llama el principio de superposición. A una amplitud suficientemente grande, el principio de superposición a menudo se descompone: las ondas que interactúan pueden dispersarse unas de otras, perder amplitud o cambiar su forma.

La interferencia es una consecuencia del principio de superposición. Cuando se superponen dos o más ondas, el desplazamiento de onda neta es solo la suma algebraica de los desplazamientos de las ondas individuales. Dado que estos desplazamientos pueden ser positivos o negativos, el desplazamiento neto puede ser mayor o menor que los desplazamientos individuales de las olas. El primer caso, que ocurre cuando ambos desplazamientos son del mismo signo, se denomina interferencia constructiva, mientras que la interferencia destructiva ocurre cuando son de signo opuesto.

Figura\(\PageIndex{1}\): .5: Superposición (panel inferior) de dos ondas sinusoidales (mostradas individualmente en el panel superior) con amplitudes y números de onda iguales\(k_{1}=4 \text { and } k_{2}=5\).

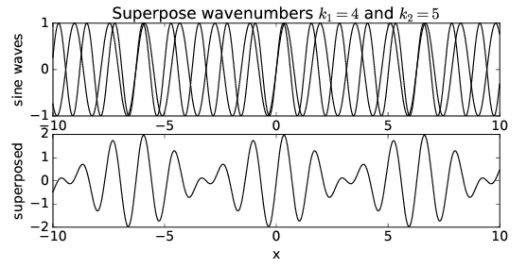
Veamos qué sucede cuando superponemos dos ondas sinusoidales con diferentes números de onda. La Figura 1.5 muestra la superposición de dos ondas con números de onda k ₁ = 4 y k ₂ = 5. Observe que el resultado es una onda con aproximadamente la misma longitud de onda que las dos ondas iniciales, pero que varía en amplitud dependiendo de si las dos ondas sinusoidales están interfiriendo constructiva o destructivamente. Nosotros decimos que las ondas están en fase si están interfiriendo constructivamente, y están fuera de fase si están interfiriendo destructivamente.

Figura\(\PageIndex{1}\): .6: Superposición de dos ondas sinusoidales con iguales amplitudes y números de onda k ₁ = 10 y k ₂ = 11.

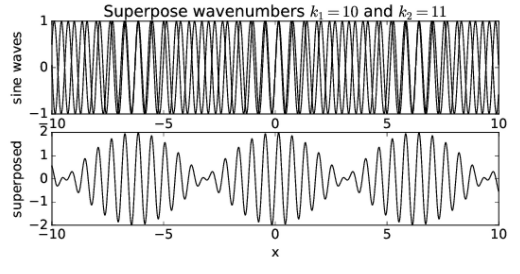
¿Qué sucede cuando se cambian los números de onda de las dos ondas sinusoidales? La Figura 1.6 muestra el resultado cuando k ₁ = 10 y k ₂ = 11. Observe que aunque la longitud de onda de la onda resultante disminuye, las ubicaciones donde la amplitud es máxima tienen la misma separación en x que en la figura 1.5.

Figura\(\PageIndex{1}\): .7: Superposición de dos ondas sinusoidales con iguales amplitudes y números de onda k ₁ = 10 y k ₂ = 12.

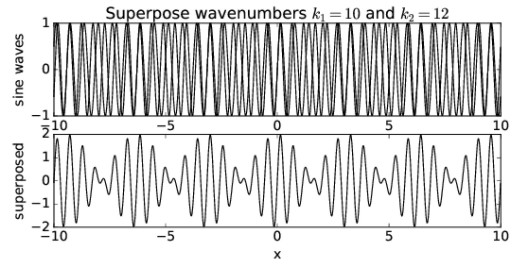
Si superponemos ondas con k ₁ = 10 y k ₂ = 12, como se muestra en la figura 1.7, vemos que el espaciamiento x de las regiones de amplitud máxima ha disminuido en un factor de dos. Así, mientras que el número de onda de la onda resultante parece estar relacionado con algo así como el promedio de los numbers de las ondas componentes, el espaciamiento entre regiones de amplitud de onda máxima parece ir inversamente con la diferencia de los numbers de las ondas componentes. En otras palabras, si k ₁ y k ₂ están muy juntas, los máximos de amplitud están muy separados y viceversa.

Figura\(\PageIndex{1}\): .8: Representación de los números de onda y amplitudes de dos ondas sinusoidales superpuestas.

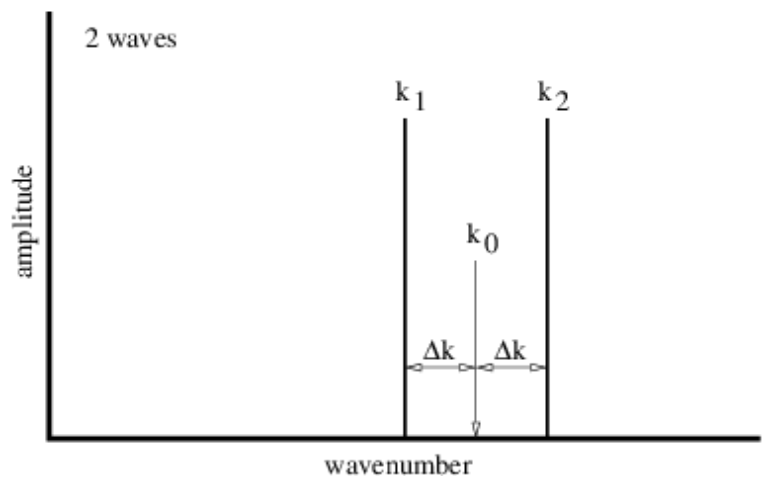
Podemos representar simbólicamente las ondas sinusoidales que componen las figuras 1.5, 1.6 y 1.7 mediante una gráfica como la que se muestra en la figura 1.8. Las amplitudes y números de onda de cada una de las ondas sinusoidales se indican mediante líneas verticales en esta figura.

Figura\(\PageIndex{1}\): .9: Superposición de veinte ondas sinusoidales con k ₀ = 4 y Δ k = 1.

Figura\(\PageIndex{1}\): .10: Representación de la distribución de números de onda y amplitudes de 20 ondas sinusoidales superpuestas con máximo a k ₀ = 4 y media anchura Δ k = 1.

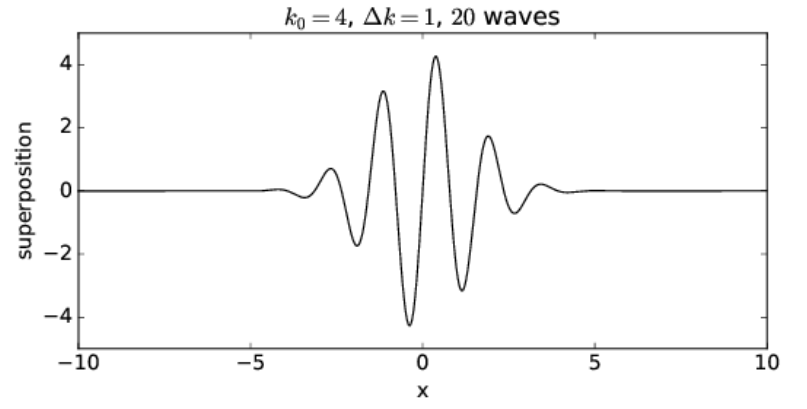
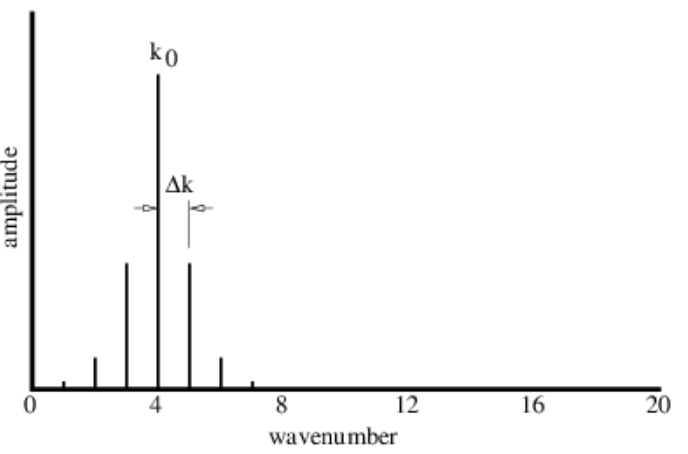
Las regiones de gran amplitud de onda se denominan paquetes de onda. Los paquetes de ondas jugarán un papel central en lo que va a seguir, por lo que es importante que adquieran una buena comprensión de ellos. Los paquetes de onda producidos por solo dos ondas sinusoidales no están bien separados a lo largo del eje x. Sin embargo, si superponemos muchas ondas, podemos producir un paquete de ondas aisladas. Por ejemplo, la figura 1.9 muestra los resultados de superponer 20 ondas sinusoidales con números de onda\(k=0.4 m, m=1,2, \ldots, 20\), donde las amplitudes de las ondas son mayores para los números de onda cercanos\(k = 4\). En particular, asumimos que la amplitud de cada onda sinusoidal es proporcional a\(\exp \left[-\left(k-k_{0}\right)^{2} / \Delta k^{2}\right]\), donde k ₀ = 4 define el máximo de la distribución de los números de onda y\(Δk = 1\) define el medio ancho de esta distribución. Las amplitudes de cada una de las ondas sinusoidales que componen el paquete de ondas en la figura 1.9 se muestran esquemáticamente en la figura 1.10.

Figura\(\PageIndex{1}\): .11: Superposición de veinte ondas sinusoidales con k ₀ = 4 y Δ k = 2.

Figura\(\PageIndex{1}\): .12: Representación de la distribución de números de onda y amplitudes de 20 ondas sinusoidales superpuestas con máximo a k ₀ = 4 y media anchura Δ k = 2.

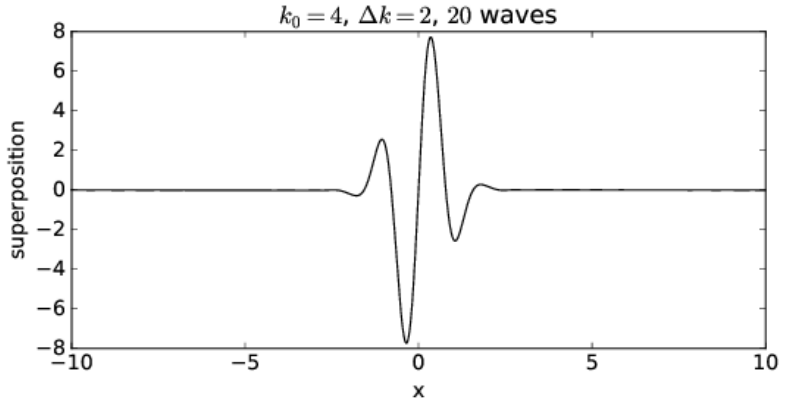
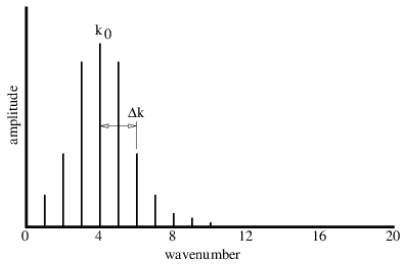
La cantidad\(Δk\) controla la distribución de las ondas sinusoidales que se superponen, solo aquellas ondas con un número de onda k dentro de aproximadamente Δk del número de onda central k ₀ del paquete de ondas, es decir, porque\(3 ≤ k ≤ 5\) en este caso, contribuyen significativamente a la suma. Si\(Δk\) se cambia a 2, de manera que los números de onda en el rango 2 ≤ k ≤ 6 contribuyen significativamente, el paquete de ondas se vuelve más estrecho, como se muestra en las figuras 1.11 y 1.12. \(Δk\)se llama propagación del número de onda del paquete de onda, y evidentemente juega un papel similar a la diferencia en los números de onda en la superposición de dos ondas sinusoidales: cuanto mayor es la propagación del número de onda, menor es el tamaño físico del paquete de ondas. Además, el número de onda de las oscilaciones dentro del paquete de ondas viene dado aproximadamente por el número de onda central.

Podemos entender mejor cómo funcionan los paquetes de ondas analizando matemáticamente el caso simple de superposición de dos ondas sinusoidales. Definamos k ₀ = (k ₁ + k ₂) 2 donde k ₁ y k ₂ son los números de onda de las ondas componentes. Además, pongamos Δk = (k ₂ - k ₁) 2. Las cantidades k ₀ y Δk se ilustran gráficamente en la figura 1.8. Podemos escribir\(k_{1}=k_{0}-\Delta k \text { and } k_{2}=k_{0}+\Delta k\) y utilizar la identidad trigonométrica\(sin(a + b) = sin(a) cos(b) + cos(a) sin(b)\) para encontrar

\ [\ comenzar {ecuación}
\ comenzar {alineado}
\ sin\ izquierda (k_ {1} x\ derecha) +\ sin\ izquierda (k_ {2} x\ derecha) =&\ sin\ izquierda [\ izquierda (k_ {0} -\ Delta k\ derecha) x\ derecha] +\ sin\ izquierda [\ izquierda (k_ {0} +\ Delta k\ derecha) x\ derecha]\
=&\ sin\ izquierda (k_ {0} x\ derecha)\ cos (\ Delta k x) -\ cos\ izquierda (k_ {0} x\ derecha) \ sin (\ Delta k x) +\\
&\ sin\ izquierda (k_ {0} x\ derecha)\ cos (\ Delta k x) +\ cos\ izquierda (k_ {0} x\ derecha)\ sin (\ Delta k x)\
=& 2\ sin\ izquierda (k_ {0} x\ derecha)\ cos (\ Delta k x)
\ fin {alineado}
\ final {ecuación}\ label {1.17}\]

El factor sinusoidal en la línea inferior de la ecuación anterior produce las oscilaciones dentro del paquete de ondas, y como se especuló anteriormente, esta oscilación tiene un número de onda k ₀ igual al promedio de los números de onda de las ondas componentes. El factor coseno modula esta onda con un espaciamiento entre regiones de amplitud máxima de

\[\Delta x=\pi / \Delta k\label{1.18}\]

Así, como observamos en los ejemplos anteriores, la longitud del paquete de ondas Δ x está inversamente relacionada con la propagación de los números de onda Δ k (que en este caso es solo la diferencia entre los dos números de onda) de las ondas componentes. Esta relación es fundamental para el principio de incertidumbre de la mecánica cuántica.