1.8: Revisión matemática — Derivados

Última actualización
Guardar como PDF

Page ID: 126129

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Esta sección proporciona una revisión rápida de la idea del derivado. A menudo nos interesa la pendiente de una línea tangente a una función y (x) a algún valor de x. Esta pendiente se llama la derivada y se denota dydx. Dado que una línea tangente a la función se puede definir en cualquier punto x, la derivada en sí misma es una función de x:

\[g(x)=\frac{d y(x)}{d x}\label{1.25}\]

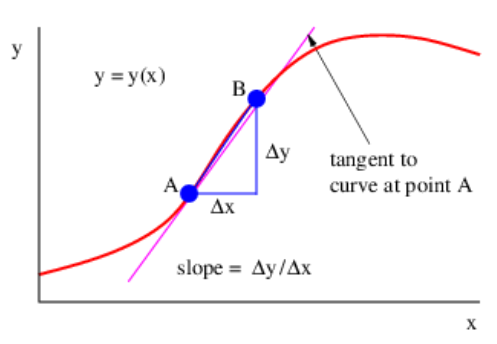
Como ilustra la figura 1.15, la pendiente de la línea tangente en algún punto de la función puede aproximarse por la pendiente de una línea que conecta dos puntos, A y B, establecer una distancia finita en la curva:

\[\frac{d y}{d x} \approx \frac{\Delta y}{\Delta x}\label{1.26}\]

A medida que B se acerca a A, la aproximación se vuelve mejor. En el límite cuando B se acerca infinitamente a A, es exacto.

Figura\(\PageIndex{1}\): Estimación de la derivada, que es la pendiente de la línea tangente. Cuando el punto B se acerca al punto A, la pendiente de la línea AB se acerca a la pendiente de la tangente a la curva en el punto A.

Ahora se dan las derivadas de algunas funciones comunes. En cada caso a es una constante.

\[\frac{d x^{a}}{d x}=a x^{a-1}\label{1.27}\]

\[\frac{d}{d x} \exp (a x)=a \exp (a x)\label{1.28}\]

\[\frac{d}{d x} \log (a x)=\frac{1}{x}\label{1.29}\]

\[\frac{d}{d x} \sin (a x)=a \cos (a x)\label{1.30}\]

\[\frac{d}{d x} \cos (a x)=-a \sin (a x)\label{1.31}\]

\[\frac{d a f(x)}{d x}=a \frac{d f(x)}{d x}\label{1.32}\]

\[\frac{d}{d x}[f(x)+g(x)]=\frac{d f(x)}{d x}+\frac{d g(x)}{d x}\label{1.33}\]

\[\frac{d}{d x} f(x) g(x)=\frac{d f(x)}{d x} g(x)+f(x) \frac{d g(x)}{d x} \quad \text { (product rule) }\label{1.34}\]

\[\frac{d}{d x} f(y)=\frac{d f}{d y} \frac{d y}{d x} \quad(\text { chain rule })\label{1.35}\]

Las reglas de producto y cadena se utilizan para calcular las derivadas de funciones complejas. Por ejemplo,

\(\frac{d}{d x}(\sin (x) \cos (x))=\frac{d \sin (x)}{d x} \cos (x)+\sin (x) \frac{d \cos (x)}{d x}=\cos ^{2}(x)-\sin ^{2}(x)\)

\(\frac{d}{d x} \log (\sin (x))=\frac{1}{\sin (x)} \frac{d \sin (x)}{d x}=\frac{\cos (x)}{\sin (x)}\).