5.3: Principio de Relatividad Aplicado

Volviendo a la fase de una ola, inmediatamente vemos que

\[\phi=\mathbf{k} \cdot \mathbf{x}-\omega t=\mathbf{k} \cdot \mathbf{x}-(\omega / c)(c t)=\underline{k} \cdot \underline{x} .\label{5.7}\]

Así, una forma compacta de reescribir la ecuación (5.2.2) es

\[A(\underline{x})=A_{0} \sin (\underline{k} \cdot \underline{x})\label{5.8}\]

Dado que se sabe que x es un cuatro vector y dado que se sabe que la fase de una onda es un escalar independiente del marco de referencia, se deduce que k también es un cuatro vector en lugar de solo un conjunto de números. Así, el cuadrado de la longitud de la onda de cuatro vectores también debe ser un escalar independiente del marco de referencia:

\[\underline{k} \cdot \underline{k}=\mathbf{k} \cdot \mathbf{k}-\omega^{2} / c^{2}=\text { const. }\label{5.9}\]

Figura 5.2: Resolución de un cuatro vectores en componentes en dos marcos de referencia diferentes.

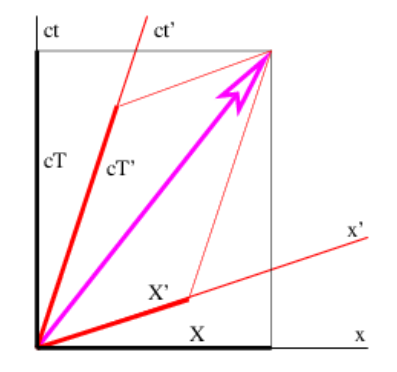
Revisemos precisamente lo que esto significa. Como muestra la figura 5.2, podemos resolver una posición de cuatro vectores en componentes en dos marcos de referencia diferentes,\(\underline{x}=(X, c T)=\left(X^{\prime}, c T^{\prime}\right)\). sin embargo, aunque\(X \neq X^{\prime} \text { and } T \neq T^{\prime}\), las longitudes de vector calculadas a partir de estos dos conjuntos de componentes son necesariamente las mismas:\(\underline{x} \cdot \underline{x}=X^{2}-c^{2} T^{2}=X^{\prime 2}-c^{2} T^{\prime 2}\).

Aplicando esto a la onda de cuatro vectores, inferimos que

\[k^{2}-\omega^{2} / c^{2}=k^{2}-\omega^{\prime 2} / c^{2}=\text { const. }\label{5.10}\]

donde los valores no cebados y cebados de k y ω se refieren a los componentes del cuatro vector de onda en dos marcos de referencia diferentes.

Hasta ahora, este argumento se aplica a cualquier ola. Sin embargo, las ondas se pueden dividir en dos categorías, aquellas para las que existe un marco de referencia “especial” y aquellas para las que no existe tal marco especial. Como ejemplo de lo primero, las ondas sonoras se ven más simples en el marco de referencia en el que el gas que transporta el sonido es estacionario. Lo mismo ocurre con la luz que se propaga a través de un medio material con un índice de refracción no igual a la unidad. En ambos casos la velocidad de la ola es la misma en todas las direcciones solo en el marco en el que el medio material es estacionario.

Supongamos que tenemos una máquina que produce una onda con número de onda k y frecuencia ω en su propio marco de descanso. Si observamos la onda desde un marco de referencia móvil, el número de onda y la frecuencia serán diferentes, digamos,\(\mathrm{k}^{\prime}\) y\(\omega^{\prime}\). Sin embargo, estas cantidades estarán relacionadas por ecuación (\ ref {5.10}).

Hasta este punto el argumento se aplica a cualquier onda ya sea que exista o no un marco de referencia especial; los cambios observados en el número de onda y la frecuencia no tienen nada que ver con la onda misma, sino que son solo consecuencias de cómo hemos elegido observarla. Sin embargo, si no hay un marco de referencia especial para el tipo de onda en consideración, entonces se puede obtener el mismo resultado manteniendo al observador estacionario y moviendo la máquina productora de olas en la dirección opuesta. Al moverlo a varias velocidades, cualquier valor deseado de se\(\mathrm{k}^{\prime}\) puede obtener en el marco de referencia inicial (a diferencia de algún otro fotograma), y el valor resultante de se\(\omega^{\prime}\) puede calcular usando la ecuación (\ ref {5.10}).

Este es en realidad un resultado asombroso. Hemos demostrado sobre la base del principio de relatividad que cualquier tipo de onda para el que no exista un marco de referencia especial puede hacerse para tomar una gama completa de frecuencias y números de onda en cualquier marco de referencia dado, y además que estas frecuencias y números de onda obedecen

\[\omega^{2}=k^{2} c^{2}+\mu^{2}\label{5.11}\]

La ecuación (\ ref {5.11}) proviene de resolver la ecuación (5.10) para\(\omega^{2}\) y la constante\(\mu^{2}\) es igual a la constante en la ecuación (\ ref {5.10}) por -c ². La ecuación (\ ref {5.11}) relaciona la frecuencia con el número de onda y por lo tanto es la relación de dispersión para tales ondas. Llamamos ondas que no tienen marco de referencia especial y por lo tanto obedecen necesariamente a la ecuación (\ ref {5.11}) ondas relativistas. La única diferencia en las relaciones de dispersión entre diferentes tipos de ondas relativistas es el valor de la constante μ. El significado de esta constante se aclarará más adelante.