1.5: Visualización y manipulación de imágenes satelitales

La mayor parte de este curso tratará sobre el tipo típico de 'imagen de satélite' que podrías ver en las noticias o en Google Earth, es decir, el tipo de imagen que producen los sensores ópticos pasivos. Estas imágenes pueden considerarse de muchas maneras similares a las fotos que tomas con tu teléfono, por lo que puedes hacer cosas similares a ellas para mejorarlas. Excepto en el contexto de la teledetección 'mejor' no significa hacer fotocompras para eliminar los ojos rojos y crear colores más vibrantes, significa mostrarlos de formas que ayuden a interpretarlos mejor para fines específicos. Esta es una forma de visualización científica, un proceso en el que mostrar datos ayuda a explorarlos y entenderlos. La razón por la que explorar los datos visualmente puede ser más útil que ejecutarlos a través de un algoritmo informático es que los humanos son excepcionalmente expertos en interpretar patrones espaciales. Como ejemplo, imagínese que está caminando por un campo en el este de Canadá y vea la escena a continuación. De inmediato eres capaz de darte cuenta de que la parte oscura de la imagen parece 'fuera de lugar' y así podría ser importante, la forma te sugiere que es un animal grande, y puedes traer todo tipo de contexto (la época del año, el medio ambiente, el hecho de que se sabe que los osos viven en la zona) para ayudar en tu interpretación de lo que está pasando.

29: Las personas son excepcionalmente buenas para reconocer estructuras en imágenes, y aunque la visión por computador está en rápido desarrollo, el cerebro humano todavía suele superar a la inteligencia artificial en este campo. Un oso en el bosque de Linda Tanner, Flickr, CC BY-NC-ND 2.0.

Pantalla en escala de grises no mejorada

Mucho sucede detrás de escena cuando se muestra una imagen en la pantalla de una computadora. Para mirar los detalles tomaremos primero el ejemplo más simple posible, una imagen en escala de grises de 8 bits, pero ten en cuenta que los mismos principios se aplican a datos de diferentes tipos. Una imagen en escala de grises de 8 bits (comúnmente, pero engañosamente, también llamada imagen en blanco y negro) corresponde a una sola capa de datos bidimensional con valores que van de 0 a 255. Digitalmente, el archivo de imagen (por ejemplo, un archivo jpg, png, tif u otro archivo de imagen) contiene un montón de números, así como cierta información sobre las dimensiones de la imagen. En el siguiente ejemplo, la imagen contiene 16 píxeles dispuestos en 4 filas y 4 columnas, y un valor entre 0 y 255 está asociado a cada celda. Este es el valor del Número Digital (DN). La mayoría de las pantallas de computadora son capaces de mostrar 256 intensidades de luz diferentes, y utilizan tres colores (rojo, verde y azul) para hacerlo, lo que permite la producción de 256 * 256 * 256 = 16.8 millones de colores. Piense en que hay tres pequeñas 'pistolas de luz de colores' dentro de cada píxel en la pantalla de la computadora, que determinan cuánta luz producir, de cada color, en cada píxel. Al mostrar imágenes en escala de grises, la intensidad de la luz producida en rojo, verde y azul es la misma, permitiendo 256 tonos de gris. El más oscuro de estos (0 intensidad de luz en rojo, 0 en verde y 0 en azul) produce un color negro en la pantalla, y el más brillante (255 en rojo, 255 en verde y 255 en azul) produce blanco. El ejemplo mostrado en la Figura 30 es así la visualización más simple (a la derecha) de los valores DN en el archivo (a la izquierda).

30: Imagen en escala de grises de una sola capa, mostrando los números digitales a la izquierda y su visualización a la derecha. Por Anders Knudby, CC BY 4.0.

Pantalla en color real no mejorada

La mayoría de las imágenes tienen más de una sola capa de datos y, por lo tanto, se pueden usar para producir imágenes en color. Las cámaras del teléfono graban archivos de imagen con tres capas, correspondientes a rojo, verde y azul, por lo que visualizar estos archivos es fácil con las tres 'pistolas de color' en la pantalla de tu computadora. Una visualización de color verdadero es, no es sorprendente, aquella en la que se muestra la capa de datos 'roja' usando la 'pistola de color' roja, y así sucesivamente. Por ejemplo:

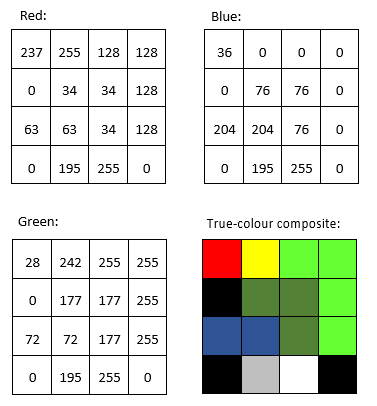
31: Valores DN en las bandas roja, verde y azul, y su visualización directa en un compuesto de color verdadero. Por Anders Knudby, CC BY 4.0.

Pantalla falso-color no mejorada

La mayoría de los sensores ópticos pasivos en los satélites registran luz en más de tres 'bandas', y así producen archivos de imagen con más de tres capas de datos. Algunas de estas bandas pueden ser de diferentes tonos de luz visible (por ejemplo, violeta), mientras que otras, como la infrarroja y la ultravioleta, caen fuera del espectro que es visible para los humanos. Para mostrar dichos datos se utilizan visualizaciones en falso color. El nombre falso color simplemente afirma que lo que se muestra no representa cómo sería el área de imágenes para un ser humano, no implica que haya nada malo con la imagen (de hecho las pantallas de falso color son muy útiles). Las pantallas de color falso vienen en muchos sabores. Imagínese la cantidad de combinaciones diferentes de tres bandas que puede hacer con los datos de un sensor que tiene más de 200 bandas... La visualización en falso color más común a menudo se llama 'color-infrarrojo', y muestra una banda de 'infrarrojo cercano' usando el rojo pistola de color, una banda 'roja' usando la pistola de color verde y una banda 'verde' usando la pistola de color azul. La Figura 32 proporciona una comparación lado a lado de color verdadero y una pantalla de color falso de una imagen Landsat que contiene la ciudad de Zanzíbar.

32: Visualizaciones de color verdadero e infrarrojo de color de una imagen Landsat que contiene la ciudad de Zanzíbar. Por Anders Knudby, CC BY 4.0.

Mejora de imagen

En los ejemplos anteriores, hemos imaginado que las imágenes siempre contenían valores entre 0 y 255, proporcionando pulcramente los 256 diferentes valores posibles que las pistolas de color en una pantalla de computadora típica pueden mostrar. Hay dos situaciones en las que usar el valor DN que se encuentra en el archivo de imagen directamente para determinar la intensidad de la luz producida por una pistola de color no es la mejor opción:

• No todos los sensores registran datos usando 8 bits por píxel (por color). Para sensores (más antiguos) que usan menos de 8 bits, o sensores (más nuevos) que usan más de 8 bits, normalmente es necesaria una conversión entre el valor DN y la intensidad con la que debe mostrarse.
• Si el sensor ha producido una imagen sobre un área particularmente brillante u oscura, o al menos si tal área es de interés específico, los valores encontrados sobre esa área (por ejemplo, entre 50 y 80) se pueden mostrar usando un rango más amplio de intensidades en la pantalla (por ejemplo, entre 20 y 110), mejorando así el contraste visual sobre el área de interés.

Para entender mejor estos problemas, debemos considerar cómo se almacenan los valores DN en la memoria de la computadora. Consideraremos un solo píxel y su valor DN para una sola banda. Para un sensor de 8 bits, este valor DN se almacena en 8 bits, cada uno de los cuales puede estar ON (1) o OFF (0). El valor se codifica como se ilustra en la Figura 33. En ese ejemplo, los bits que representan valores de 128, 32, 16, 8 y 2 están todos ON, mientras que los demás están OFF. Por lo tanto, el valor DN del píxel se calcula como 128 + 32 + 16 + 8 + 2 = 186. El rango de valores posibles con 8 bits va de 0 (todos los bits están DESCONECTADOS) a 255 (todos los bits están ENCENDIDOS), para un total de 256 valores posibles. De hecho, el número de valores posibles, dado el número de bits, se calcula fácilmente como 2 ^n, donde n es el número de bits.

33: Este ejemplo ilustra un píxel de 8 bits con el valor 186. Por Anders Knudby, CC BY 4.0.

Esta es la razón por la cual los sensores que usan menos de 8 bits para almacenar el DN para cada píxel no pueden producir 256 valores diferentes. Sin embargo, solo por el bien del argumento, si tuviéramos que mostrar valores DN de 4 bits (valores DN que oscilan entre 0 y 15) directamente sin transformación, solo veríamos tonos muy oscuros de gris (ningún sensor real registra información usando solo 4 bits, pero los primeros sensores Landsat usaron solo 6 bits, y el problema es lo mismo).

Por otro lado, los sensores que utilizan 12 bits para almacenar cada valor DN (como hacen muchos sensores modernos), contienen valores que van desde 0 hasta 2 ¹² -1 = 4095. Para mostrar este rango de valores, necesitamos transformarlos para que todos encajen entre 0 y 255, lo que se hace más fácilmente simplemente dividiendo por 16 y redondeando hacia abajo. Tenga en cuenta que en este caso, si bien la pantalla de la computadora no es capaz de mostrar los datos en todo su detalle, los algoritmos de procesamiento de imágenes seguirán siendo capaces de hacer uso de la misma.

Las cosas se ponen más interesantes cuando tenemos una imagen en la que un rango específico de valores es de mayor interés. Un ejemplo común es el tipo de imagen que se ve en la Figura 32, que contiene algo de agua (muy oscura), tierra (relativamente oscura y en gran parte verde) y nubes (muy brillantes). A menos que estemos específicamente interesados en estudiar las nubes en esta imagen, realmente no necesitamos poder distinguir entre píxeles con valores DN de 245 vs. 250 vs. 255. Lo que podemos hacer, entonces, es mostrar todos los píxeles 'brillantes' que realmente no nos importan con el mismo color (blanco), y así 'reservar' más de los diferentes brillos con los que podemos mostrar píxeles para los valores DN que más nos importan. Matemáticamente, esto significa crear una tabla que traduzca cada valor DN, para cada banda, en un valor de brillo equivalente con el que se va a mostrar en pantalla. Gráficamente, podemos mostrar esto como se hace a continuación en la Figura 34, donde se muestran los valores DN en el eje x, y el brillo con el que se muestran se muestra en el eje y. La línea azul representa el uso directo del valor DN, sin realce de contraste. La línea naranja representa una mejora de contraste lineal, en la que se muestran todos los valores DN menores a 50 con un brillo de 0, y todos los valores DN mayores a 240 se muestran con un brillo de 255. Esto nos permite utilizar los 254 valores de brillo posibles restantes para mostrar mejor las diferencias más pequeñas entre píxeles con valores DN entre 50 y 240. La línea gris es una transformación de raíz cuadrada que mantiene cierto contraste a lo largo de todo el rango de valores DN, pero se enfoca en mostrar diferencias entre píxeles con valores DN bajos, a expensas de aquellos con valores DN altos. En las Figuras 35-37 se muestran ejemplos de cómo puede verse dicha mejora de contraste en la práctica:

34: Tres opciones para mostrar datos de 8 bits. Por Anders Knudby, CC BY 4.0.

35: Sin realce de contraste. Por Anders Knudby, CC BY 4.0.

36: Mejora de contraste lineal utilizando los valores mínimo y máximo de la imagen en lugar de 50 y 240 en el ejemplo anterior. Por Anders Knudby, CC BY 4.0.

37: Mejora de contraste conocida como ecualización de histograma. Esto es matemáticamente más complejo que los ejemplos mostrados anteriormente, pero a menudo proporciona buenos resultados. Por Anders Knudby, CC BY 4.0.

Afilado de pan

Cuando ves películas de Hollywood y el analista de la CIA o el agente de policía sorprendentemente guapo hace clic en un botón para 'mejorar' las imágenes de una cámara de vigilancia, revelando así rasgos faciales de lo que antes era una mancha borrosa, bueno, eso es Hollywood. Lo que pasa con las imágenes es que son solo datos, y no se puede hacer que los detalles (nuevos datos) aparezcan donde no exista ninguno en los datos originales. Aquí hay una explicación divertida de esta idea general. Sin embargo, con algunas imágenes satelitales hay un tipo de 'realce' que en realidad funciona (aunque causa estragos de manera sutil en la radiometría de la imagen). La técnica en cuestión se llama pan-sharpening, lo que se refiere al hecho de que la mayoría de los sensores satelitales ópticos pasivos tienen una banda 'pancromática' que registra datos sobre el brillo a través de todas las bandas visibles y a mayor resolución espacial que las bandas de color individuales. Por ejemplo, los sensores de los satélites Landsat 4-7 tienen bandas azules, verdes y rojas, todas con una resolución espacial de 30 metros, y una banda pancromática que graba luz azul y verde así como roja, con una resolución espacial de 15 metros. Para los sensores modernos de alta resolución, la diferencia en la resolución espacial es aún mayor, ya que WorldView-2 tiene bandas de color a una resolución de 2 metros y una banda pancromática a una resolución de 50 cm. En términos generales, por lo tanto, podemos combinar la información de color de las bandas de color individuales con el detalle espacial de la banda pancromática, para obtener algo como lo que se ve en la Figura 38.

Existen varios algoritmos que se pueden usar para realizar esta operación, y cada uno emplea un conjunto diferente de suposiciones y reglas sobre cómo generar información de color para cada uno de los píxeles en la imagen panafilada. Si bien el contexto determina qué algoritmo es superior para una imagen dada, los resultados de la mayoría de los algoritmos son impresionantes y pueden ayudar en gran medida en la interpretación visual de las imágenes de satélite. La mayoría de los paquetes de software de procesamiento de imágenes comerciales tienen uno o más algoritmos para la nitidez panorámica, por lo que si bien el proceso en sí es bastante complejo, en realidad aplicarlo a una imagen se realiza con el clic de un botón.

Figura 7) por Fu et al, CC BY 4.0.

Relaciones de banda y otras matemáticas de banda

Las secciones anteriores se han ocupado principalmente de diferentes formas de mostrar los valores DN que se encuentran en cada banda, en escala de grises o color, directamente o transformados a través de la mejora del contraste, afilados o no. Una alternativa es crear nuevas bandas usando un proceso comúnmente llamado 'Band Math'.

Por ejemplo, podríamos querer producir una banda que cuantifique lo 'rojo' que es algo. El problema con la banda 'roja' original en una imagen típica de satélite se ve comparando los valores DN 'rojos' de la parte superior izquierda de la Figura 31 con los colores mostrados en la parte inferior derecha de la misma figura. Podría decirse que el píxel que está en la esquina superior izquierda es lo que la mayoría de la gente consideraría 'rojo', pero los dos píxeles con los valores DN más altos en la banda 'roja' son los píxeles amarillos y blancos (ambos tienen valores DN 'rojos' de 255). A pesar de su alto valor DN 'rojo', estos píxeles no aparecen 'rojos' porque también tienen valores altos de DN en uno o más de los otros colores. Para cuantificar mejor la apariencia 'roja' de cada píxel, podemos calcular algo llamado 'coordenadas cromáticas rojas' (RCC). Para cada píxel, esto se calcula como RCC = Rojo/(Rojo + Verde + Azul), donde Rojo, Verde y Azul representan los respectivos valores DN en cada píxel. Como puede ver en los cálculos de la Figura 39, el píxel rojo en la esquina superior izquierda tiene un valor de RCC mayor que cualquiera de los otros píxeles, seguido del píxel amarillo junto a él (porque el amarillo está 'cerca de' rojo). Tenga en cuenta que la matemática de banda opera en cada píxel individualmente y completa la misma operación matemática en todos los píxeles de una imagen. Al hacerlo, produce una nueva banda que es función de las bandas originales. Otros usos comunes de la matemática de bandas es calcular 'relaciones de banda', como el índice de vegetación llamado 'Relación simple' que se calcula como SR = NIR/Rojo, donde NIR es un valor (idealmente la reflectancia TOA) en la banda del infrarrojo cercano, y Rojo es el mismo valor en la banda roja. Debido a que las plantas sanas reflejan la luz infrarroja cercana de manera muy efectiva, mientras que absorben la mayor parte de la luz roja (y por lo tanto reflejan muy poca luz roja para que el sensor la detecte), las áreas con vegetación tienden a tener altos valores de reflectancia y DN en la banda del infrarrojo cercano y valores bajos en la banda roja. Esto lleva a las áreas con vegetación a tener valores de Ratio Simple muy altos, por lo que esta proporción de bandas se puede utilizar para producir rápida y fácilmente una visualización que ayude a las personas a distinguir entre áreas vegetadas y no vegetadas. Un índice de vegetación aún más popular es el Índice de Vegetación Diferencial Normalizada (NDVI), el cual se calcula como NDVI = (NIR — Rojo)/(NIR + Rojo).

Figura 31. La Coordenada Cromática Roja (RCC) se calcula como RCC = Rojo/(Rojo + Verde + Azul). A los píxeles con valores DN de 0 en todas las bandas (es decir, píxeles negros) se les han dado valores NoData (NA). Por Anders Knudby, CC BY 4.0.

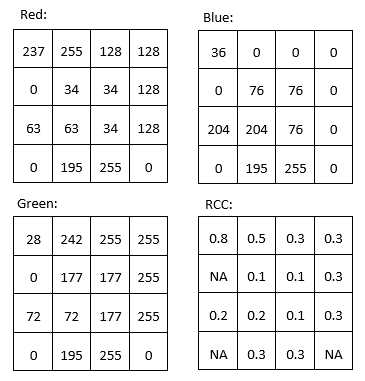
La matemática de bandas se puede usar para calcular nuevas bandas con cualquier combinación de bandas de entrada que se te ocurra, y se utilizan diferentes tipos de matemáticas de bandas, entre muchas otras aplicaciones, para monitorear la deforestación global, rastrear los cambios estacionales en la capa de nieve, mapear la profundidad del agua y monitorear la expansión urbana.

Transformación de tapa borla (TCT)

Para los datos de Landsat se ha desarrollado una aplicación particular de la matemática de bandas llamada transformación de límite borlas, y ahora se usa comúnmente para producir un conjunto de bandas estandarizadas y fácilmente interpretables a partir de los datos originales. Originalmente fue desarrollado para un instrumento llamado Landsat MSS (que ya no opera), y desde entonces se ha actualizado para Landsat TM (los sensores en Landsat 4 y 5), ETM+ (el sensor en Landsat 7) y OLI (el sensor óptico pasivo en Landsat 8). La idea detrás de la transformación de la tapa borla es producir tres nuevas bandas, 'verdor', 'brillo' y 'humedad', que describen las variaciones reales en esos parámetros a lo largo de la imagen. En una imagen satelital típica de un paisaje rural, las áreas cubiertas por agua (puntos azules) y suelo desnudo (puntos rojos) formarán una “línea” en el espacio bidimensional (NIR/RED), mientras que la vegetación (puntos verdes) se alejará de la línea y varias etapas del crecimiento de las plantas juntas formarán una forma aproximadamente como una borla tapa (Figura 40). Las tres nuevas bandas se crean rotando efectivamente los ejes del sistema de coordenadas, por lo que el 'brillo' se determina a lo largo de la 'línea de suelos' en la Figura 40, el 'verdor' se determina a lo largo de un eje que se aleja de la línea de suelos y aumenta de valor a medida que se mueve hacia la parte superior de la 'tapa borlas', y La 'humedad' se determina a lo largo de un tercer eje (no mostrado en la Figura 40) perpendicular a los dos primeros. Un ejemplo de los resultados, basado en una imagen IKONOS de Idaho, USA, se muestra en la Figura 41. En términos prácticos, cada componente de la tapa borrosa se calcula como una suma ponderada de los valores en las bandas originales. Por ejemplo, para los datos Landsat TM, el 'brillo' se calcula como BR = 0.3037 * AZUL + 0.2793 * VERDE + 0.4343 * ROJO + 0.5585 * NIR + 0.5082 * SWIR1 + 0.1863 * SWIR2 (SWIR1 y SWIR2 son dos bandas infrarrojas de onda corta también presentes en los sensores Landsat TM).

40: El principio de la transformación de la tapa borla. Los suelos desnudos de brillo variable caen a lo largo de una línea cuando se trazan con sus valores en las bandas RED y NIR, mientras que la vegetación de densidad creciente se encuentra dentro del 'casquete', arriba y a la izquierda de la línea de suelos. La vegetación en diversas etapas de crecimiento, que crece en suelos de diferente brillo, forman así una forma que parece una gorra borla. La formulación original de la gorra borla incluyó una tercera dimensión, utilizando la banda verde. Transformación de la tapa borla para suelo brillante y oscuro de Gurkengräber (adaptado de Richards y Jia), Wikimedia Commons, CC BY-SA 4.0.

41: Un ejemplo de la transformación de gorra borla aplicada a una imagen IKONOS de Idaho, EE. UU. tcap_example de Jason Karl, La caja de herramientas del paisaje, CC0 1.0.

Análisis de componentes principales (PCA)

42: Un ejemplo bidimensional de Análisis de Componentes Principales. GaussiansCatterPCA por Nicoguaro, Wikimedia Commons, CC BY 4.0.

El último tipo de matemáticas de banda que veremos en este capítulo es similar a la transformación de tapa borla en que el cálculo implica una suma ponderada de las bandas originales, pero es diferente en el sentido de que los pesos se determinan a partir de las propiedades de la imagen misma, y como tales varían de la imagen a la imagen. La Figura 42 proporciona una buena ilustración de cómo funciona. Podemos imaginar que cada punto en el diagrama de dispersión es un píxel de nuestra imagen, y que se traza de acuerdo a su valor en una banda en el eje x y otra banda en el eje y. Se desprende de la distribución de puntos en la Figura 42 que los puntos con valores altos en una banda tienden a tener también valores altos en la otra banda, y que la mayor parte de la distribución de los puntos discurre a lo largo de una línea imaginaria desde la parte inferior izquierda hasta la parte superior derecha de la gráfica. La orientación de esta línea imaginaria se llama el primer componente principal (PC ₁), y se ilustra con la flecha más larga. Pero también hay cierta variación ortogonalmente (perpendicular) a PC ₁. Esta es la orientación del segundo componente principal, PC ₂, ilustrado con la flecha más corta. Dependiendo de cuántas bandas haya en una imagen, se podría seguir encontrando nuevas líneas de este tipo en las dimensiones tercera, cuarta etc., cada una orientada a lo largo de la mayor distribución de puntos en cualquier orientación perpendicular a todos los componentes principales anteriores. En la Figura 42 el conjunto de datos original tenía sólo dos dimensiones, por lo que se crearon dos componentes principales. La longitud de cada flecha corresponde a la cantidad de distribución total capturada por cada componente principal, y es claro que PC ₂ ha capturado bastante poco de la distribución en los puntos originales. Esto se puede interpretar como PC ₂ que contiene muy poca información, y a menudo los componentes principales numerados más altos se pueden eliminar por completo con poca pérdida de información. Con este conocimiento, se pueden crear nuevas bandas, en las que el valor de cada píxel ya no es su valor DN en las bandas originales, sino su valor a lo largo de cada uno de los ejes principales de los componentes. Esta es la principal fortaleza de PCA: que permite transformar los datos en un menor número de bandas (ocupando así menos espacio en el disco duro, y permitiendo una lectura y procesamiento más rápidos) sin perder mucha información. La investigación incluso ha demostrado que para algunos tipos de imágenes (por ejemplo, una imagen Landsat libre de nubes de un área agrícola), los componentes principales específicos tienden a corresponder a variables ambientales específicas, como la humedad del suelo, la cobertura vegetal, etc. Sin embargo, aquí es importante una nota de precaución. Debido a que la orientación de los componentes principales (las flechas en la Figura 42) depende de la distribución de la totalidad de los valores de píxel en cada imagen individual, los valores de componente principal de un píxel no son directamente interpretables, y pueden variar drásticamente entre imágenes, incluso para píxeles idénticos. PCA puede así ayudarle a reducir el volumen de datos de una imagen, pero destruye (o al menos complica) la interpretación en el proceso. Otra explicación realmente buena de PCA, incluyendo una trama de dispersión animada que creo que explica las cosas muy bien, se encuentra aquí.