1.6: Clasificación

Si bien la interpretación visual de una imagen de satélite puede ser suficiente para algunos fines, también presenta deficiencias significativas. Por ejemplo, si quieres saber dónde están todas las áreas urbanas en una imagen, a) incluso a un analista de imagen experimentado tardará mucho en mirar a través de una imagen completa y determinar qué píxeles son 'urbanos' y cuáles no, y b) el mapa resultante de áreas urbanas necesariamente será algo subjetivo , ya que se basa en la interpretación del analista individual de lo que significa 'urbano' y cómo es probable que eso aparezca en la imagen. Una alternativa muy común es utilizar un algoritmo de clasificación para traducir el color observado en cada píxel en una clase temática que describa su cobertura terrestre dominante, convirtiendo así la imagen en un mapa de cobertura terrestre. Este proceso se denomina clasificación de imágenes.

Figura 1) de Wu et al., CC BY 3.0.

Se pueden identificar dos categorías de enfoques para la clasificación de imágenes. La forma tradicional y fácil es mirar cada píxel individualmente, y determinar qué clase temática corresponde a su color. Esto se suele llamar clasificación por píxel, y es lo que veremos primero. Un método más nuevo y cada vez más popular es dividir primero la imagen en segmentos homogéneos, y luego determinar qué clase temática corresponde a los atributos de cada segmento. Estos atributos pueden ser el color del segmento así como otras cosas como la forma, el tamaño, la textura y la ubicación. Esto se suele llamar análisis de imágenes basado en objetos, y lo veremos en la segunda mitad de este capítulo.

Incluso en la categoría de clasificación por píxel, hay dos enfoques diferentes disponibles. Una se llama clasificación 'supervisada', porque el analista de imagen 'supervisa' la clasificación proporcionando alguna información adicional en sus primeras etapas. Al otro se le llama clasificación 'no supervisada', porque un algoritmo hace la mayor parte del trabajo (casi) sin ayuda, y el analista de imagen sólo tiene que pisar al final y terminar las cosas. Cada uno tiene sus ventajas y desventajas, las cuales se detallarán a continuación.

Clasificación supervisada por píxel

La idea detrás de la clasificación supervisada es que el analista de imágenes proporcione a la computadora alguna información que permita la calibración de un algoritmo de clasificación. Este algoritmo se aplica entonces a cada píxel de la imagen para producir el mapa requerido. Cómo funciona esto se explica mejor con un ejemplo. La imagen que se muestra en la Figura 44 es de California, y queremos traducir esta imagen en una clasificación con las siguientes tres clases (amplias): “Urbana”, “Vegetación” y “Agua”. El número de clases, y la definición de cada clase, pueden tener un gran impacto en el éxito de la clasificación —en nuestro ejemplo estamos ignorando el hecho de que partes sustanciales del área parecen estar constituidas por suelo desnudo (y así no cae realmente en ninguna de nuestras tres clases). Y podemos darnos cuenta de que el agua en la imagen tiene un color muy diferente dependiendo de lo turbia que sea, y que algunas de las zonas urbanas son muy brillantes mientras que otras son de un tono gris más oscuro, pero estamos ignorando esos temas por ahora.

Figura 44: Compuesto de color verdadero que muestra parte de una imagen Landsat de California. En la esquina superior derecha se ve una zona urbana con un poco de agua turbia, bordeada por una mezcla de zonas vegetadas y áridas y un lago de aguas claras, y una zona montañosa en gran parte boscosa se ve en la parte inferior izquierda de la imagen, con algunas áreas despejadas brillantes cerca del centro izquierdo. Por Anders Knudby, CC BY 4.0, basado en datos de Landsat 5 (USGS).

La “supervisión” en la clasificación supervisada casi siempre viene en forma de un conjunto de datos de calibración, el cual consiste en un conjunto de puntos y/o polígonos que se sabe (o se cree) pertenecen a cada clase. En la Figura 45, dicho conjunto de datos se ha proporcionado en forma de tres polígonos. El polígono rojo perfila un área conocida por ser “Urbana”, y de manera similar el polígono azul es “Agua” y el polígono verde es “Vegetación”. Obsérvese que el ejemplo en la Figura 45 no es un ejemplo de las mejores prácticas; es preferible tener más y más pequeños polígonos para cada clase distribuidos a lo largo de la imagen, porque ayuda a los polígonos a cubrir solo píxeles de la clase prevista, y también a incorporar variaciones espaciales en p. densidad de vegetación, calidad del agua etc.

Figura 44, con tres polígonos superpuestos. El polígono rojo representa un área conocida por el analista de imagen como “Urbano”, el polígono azul es “Agua” y el polígono verde es “Vegetación”. Por Anders Knudby, CC BY 4.0.

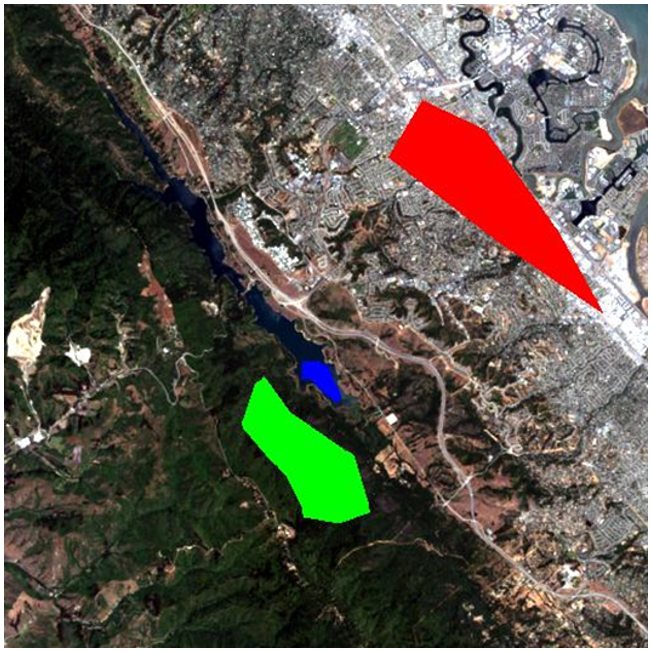
Ahora veamos cómo esos polígonos nos ayudan a convertir la imagen en un mapa de las tres clases. Básicamente, los polígonos le dicen a la computadora “mira los píxeles debajo del polígono rojo —así es como se ven los píxeles 'Urbanos'”, y la computadora puede entonces ir a buscar todos los demás píxeles de la imagen que también se ven así, y etiquetarlos como “Urbanos”. Y así sucesivamente para las otras clases. Sin embargo, algunos píxeles pueden parecer un poco “Urbanos” y un poco como “Vegetación”, por lo que necesitamos una forma matemática de averiguar a qué clase se parece más cada píxel. Necesitamos un algoritmo de clasificación.

Si tomamos todos los valores de todos los píxeles en las bandas Landsat 3 y 4 y los mostramos en una gráfica de dispersión, obtenemos algo así como la Figura 46. Esta imagen tiene una resolución radiométrica de 8 bits, por lo que los valores en cada banda teóricamente oscilan entre 0 y 255, aunque en realidad vemos que los valores más pequeños en la imagen son mayores que 0. Los valores de la banda 3 se muestran en el eje x y los valores de la banda 4 en el eje y.

Figura 44. Gráfica de dispersión creada con el software ENVI. Por Anders Knudby, CC BY 4.0.

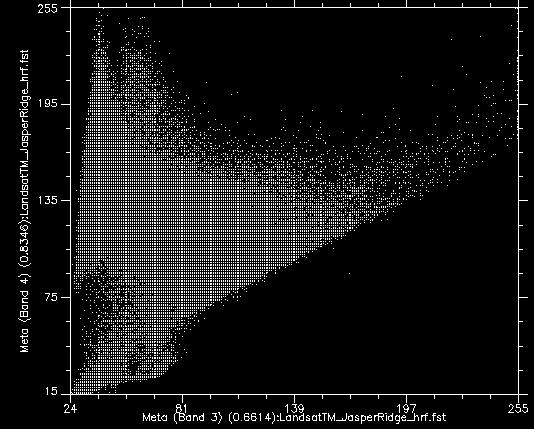
Ahora bien, si coloreamos todos los puntos que provienen de píxeles debajo del polígono rojo (es decir, los píxeles que “sabemos” que son “Urbanos”), y hacemos lo mismo con los píxeles debajo de los polígonos azul y verde, obtenemos algo así como la Figura 47. Hay algunas cosas importantes a tener en cuenta en la Figura 47. Todos los puntos azules (“Agua”) se encuentran en la esquina inferior izquierda de la figura, debajo del círculo amarillo, con valores bajos en la banda 3 y valores bajos en la banda 4. Esto es de hecho típico del agua, ya que el agua absorbe la radiación entrante en las longitudes de onda roja (banda 3) y del infrarrojo cercano (banda 4) de manera muy efectiva, por lo que muy poco se refleja para ser detectada por el sensor. Los puntos verdes (“Vegetación”) forman un área larga a lo largo del lado izquierdo de la figura, con valores bajos en la banda 3 y valores moderados a altos en la banda 4. Nuevamente, esto parece razonable, ya que la vegetación absorbe la radiación entrante en la banda roja de manera efectiva (utilizándola para la fotosíntesis) mientras refleja la radiación entrante en la banda del infrarrojo cercano. Los puntos rojos (“Urbanos”) forman un área más grande cerca del centro de la figura, y cubren un rango de valores mucho más amplio que cualquiera de las otras dos clases. Si bien sus valores son similares a los de “Vegetación” en la banda 4, generalmente son más altos en la banda 3.

Figura 46, pero con cada punto coloreado por el polígono bajo el que se encuentra. Gráfica de dispersión creada con el software ENVI. Por Anders Knudby, CC BY 4.0.

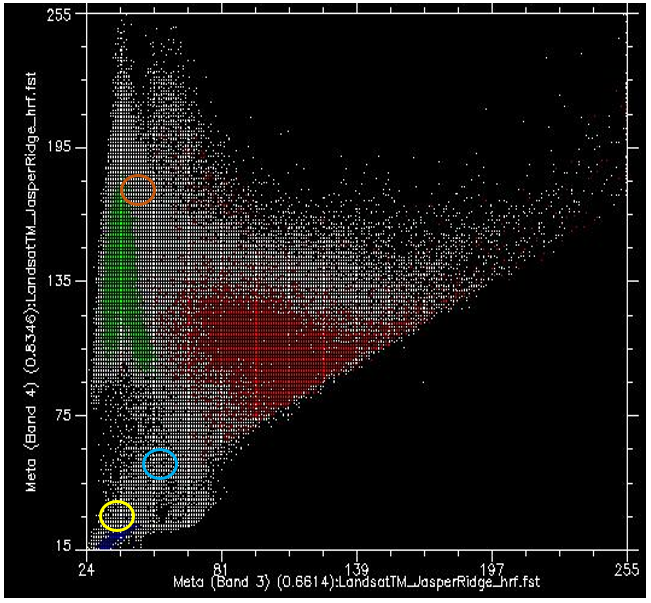
Lo que queremos que haga ahora el algoritmo de clasificación supervisada, es tomar todos los demás píxeles de la imagen (es decir, todos los puntos blancos en el diagrama de dispersión) y asignarlos a una de las tres clases en función de su color. Por ejemplo, ¿a qué clase crees que deberían asignarse los puntos blancos en el círculo amarillo de la Figura 47? Agua, probablemente. ¿Y qué pasa con los del círculo marrón claro? Vegetación, probablemente. Pero, ¿qué pasa con los del círculo azul claro? No del todo tan fácil de determinar.

Nota: El algoritmo de clasificación puede hacer uso de todas las bandas en la imagen Landsat, así como cualquier otra información que proporcionemos para toda la imagen (como un modelo digital de elevación), pero debido a que es más fácil seguir mostrando esto en dos dimensiones usando las bandas 3 y 4 solo continuaremos hazlo. Solo hay que tener en cuenta que la gráfica de dispersión es en realidad una gráfica n-dimensional, donde n es igual al número de bandas (y otras capas de datos) que queremos usar en la clasificación.

Clasificador de distancia mínima

Una forma de estimar a qué clase pertenece cada píxel es calcular la “distancia” entre el píxel y el centro de todos los píxeles que se sabe que pertenecen a cada clase, y luego asignarlo al más cercano. Por “distancia”, lo que queremos decir aquí es la distancia en “espacio característico”, en el que las dimensiones son definidas por cada una de las variables que estamos considerando (en nuestro caso las bandas 3 y 4), a diferencia de la distancia física. Nuestro espacio característico, por lo tanto, es bidimensional, y las distancias se pueden calcular utilizando una distancia euclidiana estándar.

Como ejemplo, para los puntos de la Figura 48 hemos calculado los valores medios de todos los píxeles verdes, rojos y azules para las bandas 3 y 4, y los hemos indicado con puntos grandes. Digamos que tienen los siguientes valores:

Cuadro 3: Los valores medios en las bandas 3 y 4 para las clases “Urbano”, “Vegetación” y “Agua” se muestran en la Figura 49.

Valores medios	Puntos rojos (“Urbanos”)	Puntos verdes (“Vegetación”)	Puntos azules (“Agua”)
Banda 3	100	40	35
Banda 4	105	135	20

Entonces digamos que un píxel indicado por el punto amarillo en la Figura 48 tiene un valor de 55 en la banda 3, y 61 en la banda 4. Luego podemos calcular la distancia euclidiana entre el punto y el valor medio de cada clase:

Distancia a media roja: (100-55) 2+ (105-61) 2 = 62.9

Distancia a la media verde: (40-55) 2+ (135-61) 2 = 75.5

Distancia a la media azul: (35-55) 2+ (20-61) 2 = 45.6

Debido a que la distancia euclidiana es la más corta al centro de los puntos azules, el clasificador de distancia mínima asignará este punto en particular a la clase “Azul”. Si bien el clasificador de distancia mínima es muy simple y rápido y a menudo funciona bien, este ejemplo ilustra una debilidad importante: En nuestro ejemplo, la distribución de valores para la clase “Agua” es muy pequeña: el agua es básicamente siempre oscura y azul-verde, e incluso agua turbia o agua con muchas algas en ella básicamente todavía se ve oscuro y azul-verde. La distribución de valores para la clase “Vegetación” es mucho mayor, especialmente en la banda 4, debido a que cierta vegetación es densa y otras no, alguna vegetación es saludable y otras no, alguna vegetación puede mezclarse con suelo oscuro, suelo brillante, o incluso algunas características urbanas como una carretera. Lo mismo ocurre con la clase “Urbana”, que tiene una amplia distribución de valores tanto en las bandas 3 como en la 4. En realidad, el punto amarillo en la Figura 48 no es muy probable que sea agua, porque el agua que tiene valores tan altos en ambas bandas 3 y 4 básicamente no existe. Es mucho más probable que sea un tipo inusual de vegetación, o un área urbana inusual, o (incluso más probablemente) una mezcla entre esas dos clases. El siguiente clasificador que veremos toma en cuenta explícitamente la distribución de valores en cada clase, para remediar este problema.

48: El clasificador de distancia mínima asigna la clase cuyo centro está más cercano (en el espacio de entidades) a cada píxel. El valor medio de todos los puntos rojos, en las bandas 3 y 4, está indicado por el punto rojo grande, y de manera similar para los puntos verde y azul. El punto amarillo indica un píxel que deseamos asignar a una de las tres clases. Gráfica de dispersión creada con el software ENVI. Por Anders Knudby, CC BY 4.0.

Clasificador de máxima probabilidad

Hasta hace alrededor de 10 años, el clasificador de máxima verosimilitud era el algoritmo de referencia para la clasificación de imágenes, y sigue siendo popular, implementado en todos los programas de teledetección serios, y típicamente entre los algoritmos de mejor rendimiento para una tarea determinada. Las descripciones matemáticas de cómo funciona pueden parecer complicadas porque se basan en estadísticas bayesianas aplicadas en múltiples dimensiones, pero el principio es relativamente simple: En lugar de calcular la distancia al centro de cada clase (en el espacio de entidades) y así encontrar la clase más cercana, calcularemos la probabilidad de que el píxel pertenezca a cada clase, y así encontrar la clase más probable. Lo que tenemos que hacer para que las matemáticas funcionen es hacer algunas suposiciones.

• Supondremos que antes de conocer el color del píxel, la probabilidad de que pertenezca a una clase es la misma que la probabilidad de que pertenezca a cualquier otra clase. Esto parece bastante razonable (aunque en nuestra imagen claramente hay mucho más “Vegetación” que “Agua” por lo que se podría argumentar que un píxel con color desconocido es más probable que sea vegetación que agua... esto se puede incorporar al clasificador, pero rara vez lo es, y lo ignoraremos por ahora)
• Supondremos que la distribución de valores en cada banda y para cada clase es gaussiana, es decir, sigue una distribución normal (una curva de campana).

Para comenzar con un ejemplo unidimensional, nuestra situación podría verse así si tuviéramos solo dos clases:

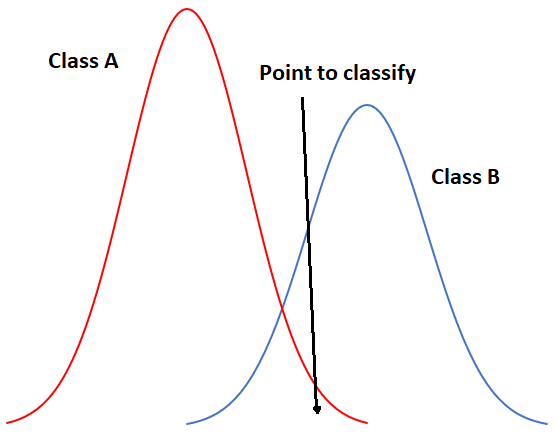
49: Ejemplo unidimensional de clasificación de máxima verosimilitud con dos clases. Por Anders Knudby, CC BY 4.0.

En la Figura 49, el eje x representa valores en una banda de imagen, y el eje y muestra el número de píxeles en cada clase que tiene un valor dado en esa banda. Claramente, la Clase A suele tener valores bajos, y la Clase B normalmente tiene valores altos, pero la distribución de valores en cada banda es lo suficientemente significativa como para que haya cierta superposición entre las dos. Debido a que ambas distribuciones son gaussianas, podemos calcular tanto la media como la desviación estándar para cada clase, y luego podemos calcular la puntuación z (cuántas desviaciones estándar estamos lejos de la media). En la Figura 49, las dos clases tienen la misma desviación estándar (las 'campanas' tienen el mismo 'ancho'), y debido a que el punto se ubica un poco más cerca de la media de la Clase B que a la Clase A, su puntuación z sería la más baja para la Clase B y se asignaría a esa clase. Un ejemplo un poco más realista se proporciona a continuación en la Figura 50, donde tenemos dos dimensiones y tres clases. Las desviaciones estándar en la banda 4 (eje x) y la banda 3 (eje y) se muestran como contornos de equiprobabilidad. El reto para el clasificador de máxima verosimilitud en este caso es encontrar la clase para la que el punto se encuentra dentro del contorno de equiprobabilidad más cercano al centro de la clase. Vea, por ejemplo, que los contornos de la Clase A y la Clase B se superponen, y que las desviaciones estándar de la Clase A son mayores que las de la Clase B. Como resultado, el punto rojo está más cerca (en el espacio de entidades) al centro de la Clase B que al centro de la Clase A, pero está en el tercer contorno de equiprobabilidad de Clase B y en la segunda de Clase A. El clasificador de distancia mínima clasificaría este punto como “Clase B” con base en la distancia euclidiana más corta, mientras que el clasificador de máxima verosimilitud lo clasificaría como “Clase A” por su mayor probabilidad de pertenecer a esa clase (según los supuestos empleados). ¿Cuál es más probable que sea correcto? La mayoría de las comparaciones entre estos clasificadores sugieren que el clasificador de máxima verosimilitud tiende a producir resultados más precisos, pero eso no es una garantía de que siempre sea superior.

50: Ejemplo bidimensional de la situación de clasificación de máxima verosimilitud, con seis clases que tienen distribuciones estándar desiguales. Por Anders Knudby, CC BY 4.0.

Clasificadores no paramétricos

Dentro de la última década más o menos, los científicos de teledetección han buscado cada vez más el campo del aprendizaje automático para adoptar nuevas técnicas de clasificación. La idea de clasificación es fundamentalmente muy genérica — tienes algunos datos sobre algo (en nuestro caso valores en bandas para un píxel) y quieres saber qué es (en nuestro caso cuál es la cobertura del suelo). Un problema difícilmente podría ser más genérico, por lo que las versiones del mismo se encuentran en todas partes: Un banco tiene alguna información sobre un cliente (edad, sexo, dirección, ingresos, historial de amortización de préstamos) y quiere saber si debe considerarse un “bajo riesgo”, “riesgo medio” o “alto riesgo” para un nuevo préstamo de 100.000 dólares. Un meteorólogo tiene información sobre el clima actual (“lluvioso, 5 °C”) y las variables atmosféricas (“1003 mb, 10 m/s viento del NW”), y necesita determinar si lloverá o no en tres horas. Una computadora tiene cierta información sobre las huellas dactilares que se encuentran en la escena de un crimen (longitud, curvatura, posición relativa, de cada línea) y necesita averiguar si son tuyas o de otra persona). Debido a que la tarea es genérica, y debido a que los usuarios fuera del ámbito de la teledetección tienen grandes cantidades de dinero y pueden usar algoritmos de clasificación para generar ganancias, los informáticos han desarrollado muchas técnicas para resolver esta tarea genérica, y algunas de esas técnicas han sido adoptadas en la teledetección. Aquí veremos un solo ejemplo, pero ten en cuenta que existen muchos otros algoritmos de clasificación genéricos que se pueden utilizar en la teledetección.

El que veremos se llama clasificador de árbol de decisiones. Al igual que con los otros clasificadores, el clasificador de árbol de decisiones funciona en un proceso de dos pasos: 1) Calibrar el algoritmo de clasificación, y 2) aplicarlo a todos los píxeles de la imagen. Un clasificador de árbol de decisión se calibra dividiendo recursivamente todo el conjunto de datos (todos los píxeles debajo de los polígonos en la Figura 45) para maximizar la homogeneidad de las dos partes (llamadas nodos). Una pequeña ilustración: digamos que tenemos 7 puntos de datos (nunca debes tener solo siete puntos de datos al calibrar un clasificador, ¡este pequeño número se usa solo con fines ilustrativos!) :

Cuadro 4: Siete puntos de datos utilizados para desarrollar un clasificador de árbol de decisiones.

Punto de datos	Valor de la banda 1	Valor de la banda 2	Clase real
1	10	30	A
2	20	40	A
3	30	40	A
4	15	55	B
5	35	40	B
6	40	35	B
7	45	35	B

La primera tarea es encontrar un valor, ya sea en la banda 1 o en la banda 2, que pueda utilizarse para dividir el conjunto de datos en dos nodos de tal manera que, en la medida de lo posible, todos los puntos de Clase A estén en un nodo y todos los puntos de la Clase B estén en el otro. Algorítmicamente, la forma en que esto se hace es probando todos los valores posibles y cuantificando la homogeneidad de las clases resultantes. Entonces, vemos que el valor más pequeño en la Banda 1 es 10, y el mayor es 45. Si dividimos el conjunto de datos según la regla de que “Todos los puntos con Banda 1 < 11 van al nodo X, y todos los demás van al nodo Y”, terminaremos con puntos divididos así:

51: Los puntos se dividen según el valor umbral 11 en la banda 1. Por Anders Knudby, CC BY 4.0.

Como podemos ver, esto nos deja con un solo punto “A” en un nodo (X), y dos puntos “A” y cuatro puntos “B” en el otro nodo (Y). Para saber si podemos hacerlo mejor, tratamos de usar el valor 12 en lugar de 11 (lo que nos da el mismo resultado), 13 (sigue siendo el mismo), y así sucesivamente, y cuando hayamos probado todos los valores en la banda 1 seguimos con todos los valores en la banda 2. Finalmente, encontraremos que usar el valor 31 en la banda 1 nos da el siguiente resultado:

52: Los puntos escupen según el valor umbral 31 en la banda 1. Por Anders Knudby, CC BY 4.0.

Esto es casi perfecto, excepto que tenemos una sola “B” en el nodo X. Pero ok, bastante bueno para una primera división. Podemos representar esto en forma de “árbol” como esta:

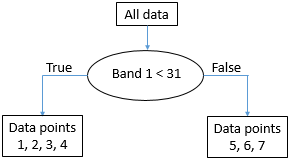
53: La estructura emergente de “árbol” a partir de la división de los datos sobre el valor umbral 31 en la banda 1. Cada colección de puntos de datos se denomina nodo. El 'nodo raíz' contiene todos los puntos de datos. A los 'nodos de hoja' también se les llama 'nodos terminales', son los puntos finales. Por Anders Knudby, CC BY 4.0.

El nodo con los puntos de datos 5, 6 y 7 (todos tienen valores de banda 1 por encima de 31) es ahora lo que se llama un “nodo puro” — consiste en puntos de datos de una sola clase, por lo que ya no necesitamos dividirlo. Los nodos que son puntos finales también se denominan “hojas”. El nodo con puntos de datos 1, 2, 3 y 4 no es “puro”, porque contiene una mezcla de puntos Clase A y Clase B. Así que pasamos de nuevo y probamos todos los diferentes valores posibles que podemos usar como umbral para dividir ese nodo (y solo ese nodo), en ambas bandas. Se da la circunstancia de que el punto de la Clase B en ese nodo tiene un valor en la banda 2 que es mayor que todos los demás puntos, por lo que un valor de división de 45 funciona bien, y podemos actualizar el árbol así:

54: La estructura final del “árbol”. Todos los nodos (partes finales del conjunto de datos) son ahora puros. Por Anders Knudby, CC BY 4.0.

Con el “árbol” en su lugar, ahora podemos tomar todos los demás píxeles de la imagen y “bajarlo” del árbol para ver en qué hoja aterriza. Por ejemplo, un píxel con valores de 35 en la banda 1 y 25 en la banda dos “irá a la derecha” en la primera prueba y así aterrizará en la hoja que contiene los puntos de datos 5, 6 y 7. Como todos estos puntos fueron de Clase B, este pixel se clasificará como Clase B. Y así sucesivamente.

Tenga en cuenta que las hojas no tienen que ser “puras”, algunos árboles dejan de dividir nodos cuando son más pequeños que un cierto tamaño, o usando algún otro criterio. En ese caso, a un aterrizaje de píxel en dicha hoja se le asignará la clase que tenga más puntos en esa hoja (y la información de que no era una hoja pura puede incluso usarse para indicar que la clasificación de este píxel en particular está sujeta a cierta incertidumbre).

El clasificador de árbol de decisión es solo uno de los muchos ejemplos posibles de clasificadores no paramétricos. Rara vez se usa directamente en la forma mostrada anteriormente, pero forma la base de algunos de los algoritmos de clasificación más exitosos en uso hoy en día. Otros algoritmos populares de clasificación no paramétrica incluyen redes neuronales y máquinas vectoriales de soporte, las cuales se implementan en gran parte del software de detección remota.

Clasificación por píxel no supervisada

¿Y si no contamos con los datos necesarios para calibrar un algoritmo de clasificación? ¿Si no tenemos los polígonos que se muestran en la Figura 45, o los puntos de datos que se muestran en la Tabla 4? ¿Qué hacemos entonces? ¡Usamos una clasificación no supervisada en su lugar!

La clasificación no supervisada procede dejando que un algoritmo divida los píxeles de una imagen en “clústeres naturales”, combinaciones de valores de banda que se encuentran comúnmente en la imagen. Una vez identificados estos clústeres naturales, el analista de imágenes puede etiquetarlos, típicamente con base en un análisis visual de dónde se encuentran estos clústeres en la imagen. El clustering es en gran parte automático, aunque el analista proporciona algunos parámetros iniciales. Uno de los algoritmos más comunes utilizados para encontrar clústeres naturales en una imagen es el algoritmo K-Means, que funciona así:

1) El analista determina el número deseado de clases. Básicamente, si quieres un mapa con alto detalle temático, puedes establecer una gran cantidad de clases. Tenga en cuenta también que las clases se pueden combinar más adelante, por lo que a menudo es una buena idea establecer el número de clases deseadas para que sea ligeramente superior a lo que cree que querrá al final. Luego se coloca aleatoriamente un número de puntos “semilla” igual al número deseado de clases en el espacio de entidades.

55: Clasificación K-Means paso 1. Un número de puntos “semilla” (puntos coloreados) se distribuyen aleatoriamente en el espacio de características. Los puntos grises aquí representan los píxeles que se van a agrupar. Modificado de K Significa Ejemplo Paso 1 por Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

2) Luego se generan clústeres alrededor de los puntos “semilla” asignando todos los demás puntos a la semilla más cercana.

56: Se forma un racimo alrededor de cada semilla asignando todos los puntos a la semilla más cercana. Modificado de K Significa Ejemplo Paso 2 por Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

3) El centroide (centro geográfico) de los puntos en cada cúmulo se convierte en la nueva “semilla”.

57: Las semillas se mueven al centroide de cada cúmulo. El centroide se calcula como el centro geográfico de cada clúster, es decir, se ubica en el valor x medio de todos los puntos del clúster, y el valor medio y de todos los puntos del clúster. Modificado de K Significa Ejemplo Paso 3 por Weston.pace, Wikimedia Commons, CC BY-SA 3.0.

4) Repita los pasos 2 y 3 hasta detener el criterio. El criterio de detención puede ser que ningún punto se mueva a otro clúster, o que el centroide de cada clúster se mueva menos de una distancia preespecificada, o que se haya completado un cierto número de iteraciones.

Otros algoritmos de clasificación no supervisados hacen el agrupamiento de manera ligeramente diferente. Por ejemplo, un algoritmo popular llamado ISODATA también permite la división de grandes clústeres durante el proceso de agrupamiento, y de manera similar para la fusión de pequeños clústeres cercanos. Sin embargo, el resultado del algoritmo de agrupamiento es que cada píxel en toda la imagen es parte de un clúster. La esperanza, entonces, es que cada cúmulo represente un tipo de cobertura terrestre que pueda ser identificado por el analista de imágenes, por ejemplo, superponiendo la ubicación de todos los píxeles del cúmulo sobre la imagen original para identificar visualmente a qué corresponde ese clúster. Ese es el paso final en la clasificación no supervisada —etiquetado de cada uno de los racimos que se han producido. Este es el paso donde puede ser conveniente fusionar racimos, si por ejemplo tienes un racimo que corresponde a agua turbia y otro que corresponde a agua clara. A menos que esté específicamente interesado en la calidad del agua, diferenciar los dos probablemente no sea importante, y fusionarlos proporcionará un producto de mapa más claro. Además, es posible que simplemente tengas dos cúmulos que ambos parecen corresponder a un bosque caducifolio saludable. Incluso si trabajas para un servicio forestal, a menos que puedas averiguar con confianza cuál es la diferencia entre estos dos clústeres, puedes fusionarlos en uno y llamarlos “bosque caducifolio”.

A modo de ejemplo, la imagen de abajo muestra la imagen original en el fondo, y los píxeles centrales coloreados según el producto de una clasificación no supervisada. Es claro que el área “azul” corresponde a píxeles cubiertos por el agua, y el área verde corresponde en gran parte a la vegetación. Sería necesario un análisis más detallado de la imagen para etiquetar cada área, especialmente las rojas y grises, de manera apropiada.

58: Ejemplo de correspondencia entre la imagen original y los conglomerados formados en un proceso de clasificación no supervisado. Por Anders Knudby, CC BY 4.0.

La clasificación de la cobertura terrestre es uno de los usos más antiguos de la teledetección, y es algo que muchos gobiernos nacionales hacen por su territorio de manera regular. Por ejemplo, en Canadá el Centro de Teledetección de Canadá trabaja con socios de Estados Unidos y México para crear un mapa de Cobertura Terrestre de América del Norte. Los mapas globales de cobertura terrestre también son producidos por diversas instituciones, como el USGS, la Universidad de Maryland, la ESA y China, por nombrar solo algunas.

Una de las deficiencias típicas de los esquemas de clasificación de imágenes que operan a nivel píxel por píxel es que las imágenes son ruidosas, y los mapas de cobertura terrestre hechos a partir de imágenes heredan ese ruido. Otra deficiencia más importante es que hay información en una imagen más allá de lo que se encuentra en los píxeles individuales. Una imagen es la ilustración perfecta del dicho de que “el conjunto es mayor que la suma de sus partes”, porque las imágenes tienen estructura, y la estructura no se toma en cuenta al mirar cada píxel independientemente del contexto proporcionado por todos los píxeles vecinos. Por ejemplo, incluso sin conocer el color de un píxel, si sé que todos sus píxeles vecinos están clasificados como “agua”, puedo decir con gran confianza que el píxel en cuestión también es “agua”. Me equivocaré de vez en cuando, pero justo la mayor parte del tiempo. Ahora veremos una técnica llamada análisis de imágenes basado en objetos que toma en cuenta el contexto a la hora de generar clasificaciones de imágenes. Esta ventaja a menudo le permite superar a los métodos de clasificación píxel por píxel más tradicionales.

Análisis de imágenes basado en objetos (OBIA)

Muchos nuevos avances en el mundo de la teledetección provienen del lado del hardware de las cosas. Se lanza un nuevo sensor, y tiene mejor resolución espacial o espectral que los sensores anteriores, o produce imágenes menos ruidosas, o se pone a disposición de manera gratuita cuando las alternativas tenían un costo. Los drones son otro ejemplo: el tipo de imágenes que producen no es sustancialmente diferente de lo que antes estaba disponible de las cámaras en aviones tripulados —de hecho suele ser inferior en calidad— pero el bajo costo de los drones y la facilidad con la que pueden ser desplegados por no expertos ha creado una revolución en términos de la cantidad de imágenes disponibles desde bajas altitudes y el costo de obtener imágenes de alta resolución para un sitio pequeño.

Uno de los pocos avances sustanciales que han llegado desde el lado del software es el desarrollo del análisis de imágenes basado en objetos (OBIA). El principio fundamental en OBIA es considerar que una imagen está compuesta por objetos en lugar de píxeles. Una ventaja de esto es que las personas tienden a ver el mundo como compuesto de objetos, no de píxeles, por lo que un análisis de imagen que adopta la misma vista produce resultados que son más fáciles de interpretar por las personas. Por ejemplo, cuando miras la Figura 59, probablemente veas el rostro de un hombre, (si lo conoces también reconocerás quién es el hombre).

59: Robert De Niro. O bien, si eres un software de análisis de imágenes basado en píxeles, un ráster de tres bandas con 1556 columnas y 2247 líneas, cada píxel y banda muestra un nivel variable de brillo. Retrato de Robert De Niro KVIFF de Petr Novák (che), Wikimedia Commons, CC BY-SA 2.5.

Debido a que se trata de una imagen digital, sabemos que en realidad está compuesta por una serie de píxeles dispuestos ordenadamente en columnas y filas, y que el brillo (es decir, la intensidad del color rojo, verde y azul en cada píxel) puede ser representado por tres números. Así podríamos clasificar las partes brillantes de la imagen como “piel” y las partes menos brillantes como “otras”, una clase mixta que comprende ojos, cabello, sombras y el fondo. ¡Sin embargo, esa no es una clasificación particularmente útil o significativa! Lo que sería más significativo sería clasificar la imagen en clases como “ojo”, “mano”, “pelo”, “nariz”, etc.

Un ejemplo algo más relevante para la teledetección se ve a continuación en la Figura 60, en la que un área urbana ha sido clasificada en objetos, entre ellos un estadio de fácil reconocimiento, calles, edificios individuales, vegetación etc.

60: Clasificación de un área urbana mediante análisis de imágenes basadas en objetos. Análisis de imágenes basado en objetos por Uddinkabir, Wikimedia Commons, CC BY-SA 4.0.

Segmentación de imágenes

El propósito de la segmentación de la imagen es tomar todos los píxeles de la imagen y dividirlos en segmentos, partes contiguas de la imagen que tienen un color similar. La segmentación de imágenes es útil porque nos aleja de analizar la imagen píxel por píxel y en su lugar nos permite analizar los segmentos individuales. Hay un par de ventajas muy importantes en esto. En primer lugar, podemos observar el “color promedio” de un segmento y usarlo para clasificar ese segmento, en lugar de usar el color de cada píxel individual para clasificar ese píxel. Si estamos tratando con imágenes ruidosas (¡y siempre lo estamos!) , el uso de promedios de segmento reduce la influencia que el ruido tiene en la clasificación. En segundo lugar, los segmentos tienen una serie de atributos que pueden ser significativos y pueden usarse para ayudar a clasificarlos — atributos que los píxeles no tienen. Por ejemplo, un segmento de imagen está formado por varios píxeles, y así podemos cuantificar su tamaño. Dado que no todos los segmentos tendrán el mismo tamaño, hay información en el atributo 'segment size' que puede ser utilizada para ayudar a clasificar los segmentos. Por ejemplo, en la Figura 60, observe que el segmento que cubre el lago es bastante grande en comparación con todos los segmentos en tierra. Eso se debe a que el lago es una parte muy homogénea de la imagen. Se observa la misma diferencia entre diferentes partes de la superficie terrestre —los segmentos justo al oeste del lago son generalmente más grandes que los del suroeste del lago, nuevamente esto se debe a que son más homogéneos, y esa homogeneidad puede decirnos algo importante sobre qué tipo de cobertura terrestre se encuentra ahí. Aparte del tamaño, los segmentos tienen una gran cantidad de otros atributos que pueden o no ser útiles en una clasificación. Cada segmento tiene un número específico de segmentos vecinos, y cada segmento también es más oscuro o más claro o en algún lugar en el medio en comparación con sus vecinos. Consulte esta página para obtener una lista de los atributos que puede calcular para los segmentos en el Módulo de extracción de características de ENVI (que no es el módulo de este tipo más completo, con diferencia). La capacidad de obtener toda esta información sobre los segmentos puede ayudar a clasificarlos, y esta información no está disponible para píxeles (por ejemplo, todos los píxeles tienen exactamente cuatro vecinos, a menos que estén ubicados en el borde de una imagen, por lo que el número de vecinos no es útil para clasificar un píxel).

Existen diferentes tipos de algoritmos de segmentación, y todos son computacionalmente complicados. Algunos son de código abierto, mientras que otros son propietarios, por lo que ni siquiera sabemos realmente cómo funcionan. Por lo tanto, no entraremos en detalles con los detalles de los algoritmos de segmentación, pero sí tienen algunas cosas en común que podemos considerar.

• Escala: Todos los algoritmos de segmentación requieren un 'factor de escala', que el usuario establece para determinar qué tan grande (es) quiere que sean los segmentos resultantes. El factor de escala no necesariamente equivale a un cierto número de píxeles, o a un cierto número de segmentos, sino que suele considerarse un número relativo. Lo que realmente significa en términos del tamaño sobre el terreno de los segmentos resultantes se encuentra típicamente por un proceso de prueba y error.
• Color vs. forma: Todos los algoritmos de segmentación necesitan tomar decisiones sobre dónde dibujar los límites de cada segmento. Debido a que generalmente es deseable tener segmentos que no tengan una forma demasiado extraña, esto a menudo implica un compromiso entre si agregar un píxel en un segmento existente si a) ese píxel hace que el color del segmento sea más homogéneo pero también da como resultado una forma más extraña, o b) si ese píxel hace que el color del segmento menos homogéneo pero da como resultado una forma más compacta. Uno o más parámetros suelen controlar esta compensación, y en cuanto al parámetro 'escala', encontrar la mejor configuración es cuestión de prueba y error.

En un mundo ideal, la segmentación de la imagen produciría segmentos que correspondían cada uno a uno, y exactamente a un objeto del mundo real. Por ejemplo, si tienes una imagen de un área urbana y quieres mapear todos los edificios, el paso de segmentación de la imagen idealmente resultaría en que cada edificio sea su propio segmento. En la práctica eso suele ser imposible porque el algoritmo de segmentación no sabe que estás buscando edificios... si estuvieras buscando mapear tejas, tener segmentos que correspondan a un techo entero sería inútil, como sería si estuvieras buscando mapear cuadras de ciudades. “Pero podría establecer el factor de escala en consecuencia” se podría decir, y eso es cierto hasta cierto punto. ¡Pero no todos los techos son del mismo tamaño! Si estás mapeando edificios en una imagen que contenga tanto tu propia casa como el Pentágono, es poco probable que encuentres un factor de escala que te dé exactamente un segmento que cubra cada edificio... La solución a este problema suele ser alguna intervención manual, en la que los segmentos producidos por la inicial la segmentación se modifican de acuerdo a reglas específicas. Por ejemplo, puede seleccionar un factor de escala que funcione para su casa y dejar el Pentágono dividido en 1000 segmentos, para luego fusionar posteriormente todos los segmentos vecinos que tengan colores muy similares. Suponiendo que el techo del Pentágono es bastante homogéneo, eso fusionaría todos esos segmentos, y asumiendo que tu propia casa está rodeada de algo de aspecto diferente, como una calle, un patio trasero o una entrada, tu propio techo no se fusionaría con sus segmentos vecinos. Esta capacidad de jugar manualmente con el proceso para lograr los resultados deseados es a la vez una gran fortaleza y una debilidad importante del análisis de imágenes basado en objetos. Es una fortaleza porque permite a un analista de imagen producir resultados que son extremadamente precisos, pero una debilidad porque incluso a los analistas expertos les toma mucho tiempo hacer esto por cada imagen. Un ejemplo de una buena segmentación se muestra en la Figura 61, que también ilustra la influencia de los cambios en los parámetros de segmentación (compare las imágenes inferior izquierda e inferior derecha).

Cabe señalar aquí que el análisis de imágenes basado en objetos se desarrolló inicialmente y se utilizó ampliamente en el campo de la imagen médica, para analizar imágenes de rayos X, células vistas bajo microscopios, etc. Dos cosas son bastante diferentes entre las imágenes médicas y la teledetección: En las imágenes médicas, la salud de las personas se ve muy directamente afectada por el análisis de imágenes, por lo que el hecho de que se necesite más tiempo para obtener un resultado preciso es menos restrictivo que en la teledetección, donde los impactos humanos de los pobres los análisis de imágenes son muy difíciles de evaluar (aunque en última instancia pueden ser igual de importantes). El otro problema es que las imágenes estudiadas por los médicos se crean en entornos altamente controlados, prácticamente sin ruido de fondo, el objetivo de la imagen siempre enfocado, y se pueden rehacer si es difícil de analizar. En la teledetección, si la neblina, la mala iluminación, el humo u otros factores ambientales se combinan para crear una imagen ruidosa, nuestra única opción es esperar hasta la próxima vez que el satélite vuelva a pasar sobre el área.

Figura 6) de Chen et al., CC BY 4.0.

Clasificación de segmentos

La clasificación de segmentos podría, en teoría, seguir los enfoques supervisados y no supervisados descritos en el capítulo sobre clasificación por píxel. Es decir, las áreas con cobertura terrestre conocida podrían usarse para calibrar un clasificador basado en un conjunto de atributos de segmento predeterminados (enfoque supervisado), o un conjunto de atributos predeterminados podría usarse en un algoritmo de agrupamiento para definir clústeres naturales de segmentos en la imagen, que luego podrían etiquetarse mediante el analista de imagen (enfoque no supervisado). Sin embargo, en la práctica, el análisis de imágenes basado en objetos a menudo procede de una manera más interactiva. Un enfoque común es que un analista desarrolla un conjunto de reglas que se estructura como un árbol de decisiones, ve qué resultado produce ese conjunto de reglas, modifica o agrega a él, y vuelve a verificar, todo en un proceso iterativo muy intensivo del usuario. Esta es una de esas áreas donde la teledetección parece más un arte que una ciencia, porque los analistas de imagen adquieren experiencia con este proceso y se vuelven cada vez mejores en él, básicamente desarrollando su propio 'estilo' de desarrollar los conjuntos de reglas necesarios para lograr una buena clasificación. Por ejemplo, después de haber segmentado una imagen, es posible que desee separar las superficies artificiales (carreteras, aceras, estacionamientos, techos) de la superficie natural, lo que normalmente puede hacerlo porque las primeras tienden a ser grises y las segundas tienden a no serlo. Entonces desarrollas una variable que cuantifica qué tan gris es un segmento (por ejemplo, usando el valor de “saturación” de HSV, más información aquí), y encuentras manualmente un valor umbral que separe efectivamente las superficies naturales de las artificiales en tu imagen. Si estás haciendo estudios urbanos, es posible que también quieras diferenciar entre los diferentes tipos de superficies hechas por el hombre. Todos son grises, así que con un clasificador basado en píxeles ahora no tendrías suerte. Sin embargo, se trata de segmentos, no de píxeles, por lo que cuantifica qué tan alargado es cada segmento y define un valor de umbral que le permite separar carreteras y aceras de techos y estacionamientos. Entonces usas el ancho de los segmentos alargados para diferenciar las carreteras de las aceras, y finalmente usas el hecho de que los estacionamientos tienen segmentos vecinos que son carreteras, mientras que los techos no, para separar esos dos. Encontrar todas las variables adecuadas para usar (valor de saturación HSV, elongación, ancho, clase de segmento vecino) es un ejercicio inherentemente subjetivo que implica prueba y error y en el que se mejora con la experiencia. Y una vez que haya creado una primera estructura de árbol de decisiones (o similar) para su conjunto de reglas, es muy probable que sus ojos se vean atraídos por uno o dos segmentos que, a pesar de sus mejores esfuerzos, todavía estaban mal clasificados (tal vez esté el techo ocasional que se extiende hasta ahora sobre la casa que su vecina segmento es de hecho una carretera, por lo que se desclasificó como un estacionamiento). Ahora puedes pasar y crear reglas adicionalmente sofisticadas que remedien esos problemas específicos, en un proceso que solo termina cuando tu clasificación es perfecta. Esto es tentador si te enorgulleces de tu trabajo, pero consume mucho tiempo, y también termina dando como resultado un conjunto de reglas que es tan específico que solo funciona para la única imagen para la que fue creada. La alternativa es mantener el conjunto de reglas más genéricas que era imperfecto pero que funcionaba bastante bien, y luego cambiar manualmente la clasificación para aquellos segmentos que sabes terminaron mal clasificados.

En resumen, la clasificación de imágenes basada en objetos es una metodología relativamente nueva que se basa en dos pasos: 1) dividir la imagen en segmentos contiguos y homogéneos, seguido de 2) una clasificación de esos segmentos. Se puede utilizar para producir clasificaciones de imágenes que casi siempre superan a las clasificaciones por píxel en términos de precisión, pero también requieren sustancialmente más tiempo para que un analista de imágenes las lleve a cabo. El primer, mejor y más utilizado software para OBIA en el campo de la teledetección es eCOGNITION, pero otros paquetes de software comerciales como ENVI y Geomatica también han desarrollado sus propios módulos OBIA. Los paquetes de software GIS como ArcGIS y QGIS proporcionan herramientas de segmentación de imágenes, así como herramientas que se pueden combinar para realizar la clasificación de segmentos, pero generalmente proporcionan flujos de trabajo OBIA menos optimizados. Además, al menos un paquete de software de código abierto ha sido diseñado específicamente para OBIA, y las herramientas de segmentación de imágenes están disponibles en algunas bibliotecas de procesamiento de imágenes, como OTB.