1.8: Detección de cambios

Gran parte del cambio ambiental ocurre a escalas temporales y espaciales que hacen que sea desafiante y potencialmente costoso de estudiar. Ejemplos obvios incluyen algunas de las manifestaciones del cambio climático: el aumento de las temperaturas y el derretimiento del hielo en el Ártico y los sutiles cambios de vegetación que ocurren en todo Canadá, por nombrar algunos. Monitorear estas cosas exclusivamente con mediciones de campo sería increíblemente costoso, o fuertemente sesgado hacia áreas pobladas y, cuando las mediciones históricas no están disponibles, imposible. Los datos de teledetección vienen aquí al rescate, porque la fotografía aérea y las imágenes satelitales se almacenan y catalogan de manera rutinaria y así pueden funcionar como datos tanto del pasado como del presente, siempre y cuando podamos extraer de ellos la información necesaria. Imagínese responder estas preguntas con confianza sin tener acceso a los datos de teledetección:

• ¿La superficie anual quemada por incendios forestales aumenta o disminuye en Canadá?
• ¿Qué parte de Canadá está calentando más rápido?
• ¿Dónde hay todavía hielo de varios años en el Ártico y qué tan rápido se está reduciendo esa área?

Antes de comenzar a usar datos de teledetección para detectar cambios ambientales, es útil considerar lo que queremos decir con eso, ¿qué es el cambio ambiental? El ambiente cambia todo el tiempo —está nevando afuera mientras escribo esto y no nevó hace dos días— ese es un tipo de cambio ambiental, pero no del tipo que la mayoría de la gente quiere detectar y mapear con datos de teledetección. Sin embargo, es exactamente ese tipo de cambio el que es visible en imágenes de la Tierra desde el espacio, así que nos guste o no detectamos muchos cambios irrelevantes con datos de teledetección. Para pensar mejor qué cambio queremos detectar y qué cambio no, una distinción útil para hacer es entre cambio a corto plazo/instantáneo y cambio gradual a largo plazo/cambio gradual. A veces nos interesa encontrar el cambio a corto plazo, mientras que en otras ocasiones, cuando estamos más preocupados por tendencias graduales más largas, lo consideramos ruido.

Cambio instantáneo

La teledetección puede ser efectiva para detectar cambios instantáneos, es decir, cambios que ocurren entre una adquisición de imagen y la siguiente. Este cambio puede no ser necesariamente instantáneo en el sentido estricto de la palabra, pero para fines prácticos de teledetección un cambio que ocurre en el período entre dos adquisiciones de imágenes puede considerarse 'instantáneo'. La detección de tal cambio suele realizarse con bastante facilidad con la interpretación visual de dos imágenes, comparándolas una al lado de la otra para identificar fácilmente las áreas de cambio. Un ejemplo de este tipo de comparación se muestra en la Figura 63, que muestra los cambios en una zona urbana de Taiwán entre febrero (izquierda) y diciembre (derecha) de 2002. La vegetación (áreas rojas) ha cambiado claramente en algunos lugares, al igual que algunas de las otras áreas. También se han desarrollado muchos algoritmos de procesamiento de imágenes para este propósito, para automatizar el proceso de búsqueda de las áreas que han cambiado; los veremos más adelante en este capítulo.

63: Ejemplo de comparación lado a lado de dos imágenes que muestran la ciudad de Zanzíbar en 1995 (izquierda) y 2020 (derecha). La expansión urbana que se ha producido en el periodo entre las dos imágenes adquiridas se puede identificar visual o algorítmicamente. Por Anders Knudby, CC BY 4.0.

Cambio gradual

La comparación visual u otra imagen-imagen puede ser efectiva para resaltar cambios abruptos obvios como los causados por el desarrollo urbano, deslizamientos de tierra, incendios forestales, etc. Sin embargo, un cambio más sutil, como la variación anual o decadal en la humedad del suelo o la salud de la vegetación, o el cambio en la profundidad de la capa de nieve invernal, a menudo requiere un enfoque diferente para la detección de cambios, uno que se base en el análisis cuantitativo de los cambios observados en muchas imágenes. Este es especialmente el caso cuando los cambios individuales de imagen a imagen pueden oscurecer la tendencia más gradual a largo plazo debido a patrones relacionados con el clima o estacionales. Por ejemplo, para estudiar cómo el cambio climático está afectando los patrones de vegetación en el Ártico canadiense, una comparación de dos imágenes proporciona, en el mejor de los casos, una instantánea de los años de procedencia de esas imágenes, y en el peor simplemente nos dice que en 2002 (agosto) hay más vegetación que en 1994 (febrero), que realmente no tiene nada que ver con un cambio entre los dos años sino más bien es una función de la época del año en que se adquirió cada imagen. De cualquier manera, tales comparaciones de imagen a imagen no nos dicen mucho sobre la tendencia a largo plazo. En cambio, una medida de la variable de interés (por ejemplo, densidad de vegetación o salud) debe cuantificarse a intervalos regulares durante un largo período de tiempo para detectar tales tendencias. Un ejemplo se proporciona en la Figura 64, en la que la extensión del Hielo Marino Ártico se ha cuantificado casi diariamente para el periodo 1979 — 2018.

64: Estimaciones casi diarias de la extensión del Hielo Marino Ártico. Extensión del hielo marino ártico por M. Scott, Centro Nacional de Datos de Nieve y Hielo (NSIDC), NSIDC Uso y Derechos de Autor.

La metodología específica utilizada para detectar el cambio gradual a largo plazo depende completamente del tipo de cambio en cuestión (por ejemplo, cambio de vegetación vs. cambio de hielo marino), por lo que es difícil proporcionar detalles sobre cómo detectar el cambio en este caso. Sin embargo, una preocupación central para cualquier tipo de 'detección de tendencias' es que la estimación (por ejemplo, de la extensión del hielo marino) debe ser relativamente imparcial durante todo el período de observación. En otras palabras, la extensión del hielo marino no debe estar subestimada ni sobreestimada en el periodo 1979-1989, y tampoco debe ser subestimada o sobreestimada en la década de 2010, ni en ningún momento intermedio. Esto es importante para evitar 'detectar' tendencias que son causadas por sesgos en la adquisición o procesamiento de datos, pero que no existen en la realidad.

Separar el ruido del cambio instantáneo real

Al comparar una imagen con otra con la intención de detectar cambios entre ellas, el principal desafío es detectar cambios ambientales reales sin detectar cambios que en realidad no han ocurrido. Como siempre ocurre en la clasificación binaria (de la que este es un ejemplo), existen cuatro combinaciones posibles de realidad (cambio o no cambio) y estimación (cambio detectado vs. no cambio detectado, Tabla 14):

Cuadro 14: Una clasificación binaria (una que involucra dos opciones categóricas) se puede describir con una tabla como esta. Para cualquier sistema de procesamiento de imágenes, el reto en la clasificación binaria es optimizar el número/tasa de verdaderos positivos y verdaderos negativos.

	Cambio detectado	No se detectaron cambios
Cambiar	Verdadero positivo (TP)	Falso negativo (FN)
Sin cambios	Falso positivo (FP)	Verdadero negativo (TN)

El objetivo, entonces, es optimizar la velocidad a la que se encuentran verdaderos positivos y verdaderos negativos. La mayoría de los algoritmos de detección de cambios operan píxel a píxel, por lo que esto significa detectar correctamente los píxeles que realmente han cambiado sin 'detectar' incorrectamente el cambio en píxeles que no han cambiado. Para ello, necesitamos una forma de separar tres situaciones diferentes, cada una de las cuales puede ocurrir en un píxel dado:

• Sin cambios: el píxel literalmente se ve exactamente igual en cada imagen.
• Ruido: El píxel se ve diferente en las dos imágenes, pero la diferencia es lo suficientemente pequeña como para que probablemente sea causada por factores no relacionados con el cambio ambiental real. Estos pueden incluir diferencias en las condiciones atmosféricas entre las dos imágenes, ruido aleatorio en las imágenes, georreferenciación imperfecta y otros temas.
• Cambio real: El cambio ambiental real ha ocurrido en el píxel, y se muestra como una diferencia sustancial entre cómo se ve el píxel en la primera imagen y en la segunda imagen.

La primera situación, sin cambios, ocurre muy raramente porque hay ruido inherente al proceso de creación de imágenes, y es poco probable que este ruido sea idéntico entre dos imágenes diferentes. El verdadero reto, entonces, es separar las situaciones 2) y 3). Hay dos principios involucrados en hacer esto.

Reducción de ruido

En primer lugar, es importante eliminar tantas fuentes de ruido como sea posible antes de comparar los datos en las dos imágenes. Algunas estrategias que a menudo se emplean con este fin incluyen:

• Utilice 'fechas de aniversario'. Elija dos imágenes que fueron capturadas en la misma fecha (o casi) en diferentes años. Esta es una buena manera de eliminar grandes diferencias entre cada imagen relacionadas con los cambios estacionales en la humedad del suelo, el estado de la vegetación, la capa de nieve y otros factores ambientales que cambian con las estaciones.
• Utilice imágenes capturadas por el mismo sensor. Dado que ningún sensor está perfectamente calibrado, el uso de imágenes de dos sensores diferentes podría introducir una diferencia basada en sensores en lugar de basada en el entorno. Por ejemplo, si la radiancia en el espectro de 500-600 nm es ligeramente sobreestimada por un sensor y ligeramente subestimada por otro sensor, comparar imágenes entre los dos puede 'detectar cambios' donde no existe ninguno.
• Utilizar imágenes capturadas en estados atmosféricos similares. Esto es difícil porque a menudo no tenemos información precisa sobre cargas de aerosoles, vapor de agua, velocidad del viento, etc., pero definitivamente evitamos comparar imágenes con diferencias obvias en neblina, visibilidad y otros factores atmosféricos visibles.
• Compare las imágenes en función de su reflectancia superficial en lugar de la radiancia TOA o la reflectancia TOA. Esto se debe a que la reflectancia superficial es un atributo físico de la superficie, y es al menos en principio independiente del estado atmosférico y de la iluminación.
• Para sensores de inclinación, si es posible, compare las imágenes tomadas con más o menos la misma geometría.

Identificar un umbral

Una vez que se hayan eliminado tantas fuentes de ruido como sea posible, y las imágenes se hayan convertido en reflectancia superficial para su comparación, todavía habrá algo de ruido que haga que los valores de reflectancia superficial en las dos imágenes difieran ligeramente entre las imágenes, incluso para píxeles que no hayan experimentado el tipo de cambio que queremos detectar. Para separar las situaciones 2) y 3) anteriores, por lo tanto, es importante considerar qué significa el cambio ambiental “real” y definir un umbral por debajo del cual cualquier 'cambio' observado en la comparación de imágenes se considera 'ruido' en lugar de 'cambio real'. Por ejemplo, imagina que estás estudiando cambios en la vegetación, y tienes dos imágenes del mismo bosque. El verdadero cambio que ocurrió entre estas dos imágenes es que una hoja se cayó de uno de los árboles del bosque. Este es un cambio observable real en el ambiente, ¡pero en cualquier sentido real no justifica la etiqueta de 'deforestación'! Un requisito previo para separar las situaciones 2) y 3) anteriores es definir cuánto cambio se requiere para que consideres el área 'cambiada'. A menos que tengas observaciones de campo (y normalmente no lo hagas porque el cambio se detecta hacia atrás en el tiempo y no puedes ir a obtener datos de campo del pasado), esto requiere definir el umbral en función de las propias imágenes, algo que suele ser un proceso interactivo y subjetivo.

Métodos para detectar cambios instantáneos

Algunos de los enfoques más simples para detectar la magnitud del cambio se basan en las 'matemáticas de imagen'.

Diferencia de banda

Por ejemplo, la magnitud del cambio se puede definir como la diferencia entre los valores de reflectancia superficial en la banda 1 en las dos imágenes, más la diferencia en la banda 2, etc.:

Cambio = (B1 _I2 -B1 _I1) + (B2 _{I2 -B2 I1})...

Relación de banda

O se pueden usar proporciones en lugar de diferencias:

Cambio = (B1 _I2 /B1 _I1) + (B2 _I2 /B2 _I1)...

Distancia euclidiana

Un método más utilizado es calcular la 'distancia euclidia', utilizando cada banda como dimensión y cada imagen como punto. Imagine que traza las reflectancias superficiales de cada imagen como puntos en un sistema de coordenadas. La distancia euclidiana entre ellos sería entonces igual:

Cambio = (B1 _I2 -B1 _I1) ² + (B2 _{I2 -B2 I1}) ²...

Para cada uno de estos enfoques, para separar el ruido del cambio ambiental real, será necesario definir un valor umbral. Los píxeles que no hayan experimentado ningún cambio o cambio menor que el valor umbral se considerarán entonces efectivamente 'inalterados', mientras que aquellos que hayan experimentado más cambios se considerarán que contienen 'cambio real'. También tenga en cuenta que para cada una de estas aproximaciones, el número de bandas involucradas en el cálculo se han limitado a dos en las ecuaciones anteriores, pero pueden extenderse para incluir cualquier número de bandas presentes en las imágenes.

Métodos para detectar y atribuir cambios instantáneos

Los tres enfoques anteriores pueden ser efectivos para detectar cambios, pero también todos sufren el inconveniente de que nos dicen muy poco sobre el tipo de cambio que ha ocurrido en un píxel dado. Si bien la detección de cambios es un gran primer paso, no es fácil basar las decisiones de gestión, por lo que es útil averiguar un poco más sobre el tipo de cambio que se ha detectado, llamado atribución de cambio.

Cambiar vectores

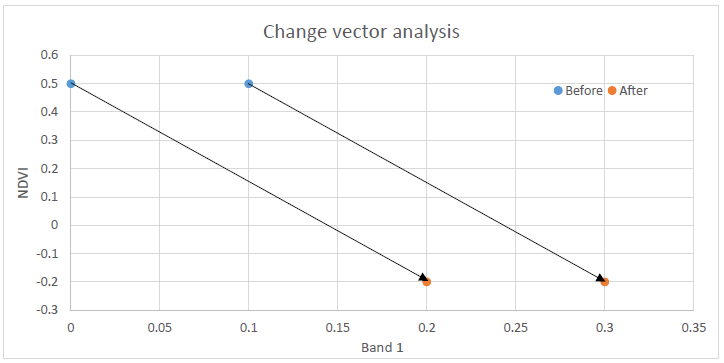
Los vectores de cambio pueden ayudar con esto. El análisis vectorial de cambio es una extensión del cálculo de la distancia euclidiana, en la que también se calcula la dirección del cambio. Un ejemplo con sólo dos dimensiones se proporciona en la Figura 65. En la imagen 'antes', el valor de reflectancia superficial en la banda 1 es 0.1, y el valor NDVI es 0.5. En la imagen 'después', estos valores han cambiado a 0.3 y -0.2 respectivamente. Esto ilustra dos cosas: 1) no es necesario usar valores de banda reales como entradas para cambiar los análisis de detección, y 2) la dirección del cambio: se puede encontrar un aumento en la reflectancia de la banda 1, una disminución en el NDVI.

En el análisis de vectores de cambio, la magnitud del cambio se calcula como la distancia euclidiana, según la ecuación anterior. La dirección del cambio se puede calcular en grados (por ejemplo, dirección de la brújula) o, para facilitar la interpretabilidad, en direcciones principales: A) arriba y derecha, B) abajo y derecha, C) abajo e izquierda, D) arriba e izquierda. Si las 'bandas' utilizadas pueden interpretarse de manera significativa, atribuir el cambio puede ser fácil. Los cambios que implican una disminución en un índice de vegetación implican una pérdida de vegetación, mientras que aquellos que conducen a un aumento en, digamos, la temperatura superficial implican, bueno, un aumento en la temperatura de la superficie (estos dos suelen ir juntos porque la vegetación ayuda a mantener una superficie fresca). Si bien calcular la distancia euclidiana es fácil cuando se utilizan más de dos dimensiones en el análisis de vectores de cambio (solo se extiende la ecuación para que contenga más términos), la dirección del cambio se vuelve más difícil de definir y las categorías se desarrollan típicamente para una aplicación específica. Al igual que con los métodos simplemente utilizados para detectar el cambio, se puede aplicar un umbral a la magnitud del vector de cambio, por debajo del cual se detecta 'no cambio'.

65: Ejemplo de análisis de vectores de cambio con solo dos bandas. NDVI es el Índice de Vegetación de Diferencia Normalizada, descrito con más detalle en el siguiente capítulo. Anders Knudby, CC BY 4.0.

66: Un inconveniente del análisis de vectores de cambio es que dos vectores de cambio idénticos pueden representar diferentes tipos de cambio. Anders Knudby, CC BY 4.0.

Un inconveniente del análisis de vectores de cambio es que dos cambios diferentes pueden tener exactamente el mismo vector de cambio. Para un ejemplo, fíjese en las dos flechas de la Figura 66. Si bien los dos vectores son idénticos —tienen la misma dirección y magnitud—, es probable que representen diferentes tipos de cambio porque comienzan y terminan en diferentes lugares. Por lo tanto, es difícil, en la práctica a menudo imposible, utilizar el análisis de vectores de cambio para determinar específicamente cuál era la superficie antes y después del cambio.

Detección de cambio posterior a la clasificación

Probablemente la forma más sencilla de detectar y cambiar de atributo en un área es realizar una clasificación de cobertura terrestre en la imagen del “antes”, realizar otra clasificación de cobertura terrestre en la imagen del “después” y luego encontrar píxeles que se clasificaron de manera diferente en las dos imágenes. Si bien esto es atractivo y sencillo, y puede funcionar ocasionalmente, está sujeto a un inconveniente importante: Es muy difícil producir resultados precisos de esta manera. La razón es que ninguna clasificación es perfecta, y al comparar dos clasificaciones imperfectas los errores se combinan. Por lo tanto, sugiero encarecidamente que se evite este enfoque.

Cambiar clasificación

Si realmente quieres saber cuál era el área cambiada antes y después del cambio, una alternativa a la detección de cambios post-clasificación es combinar todas las bandas de las dos imágenes en una sola imagen. Por ejemplo, si tienes dos imágenes, cada una con seis bandas, podrías 'apilarlas' para obtener una sola imagen de 12 bandas. Esto le permite ejecutar una sola clasificación en la imagen de 12 bandas. Con buenos datos de campo para calibrar esta clasificación, cada clase se puede definir de acuerdo con la combinación de coberturas terrestres antes y después. La clasificación puede ser supervisada o no supervisada, basada en píxeles o basada en segmentos. Este enfoque permite que los dos vectores de la Figura 66 terminen en dos clases diferentes, donde tal vez uno es un cambio de bosque de coníferas a pantano mientras que el otro es un cambio de bosque caducifolio a pantano.

Cambiar clasificación también permite eliminar combinaciones de clases que son imposibles o muy improbables, como un cambio de 'océano' a 'bosque de coníferas', o de 'industria' a 'humedad'. Decidir qué combinaciones antes y después de clases son probables y cuáles son poco probables en un área determinada requiere cierta experiencia, y los complejos sistemas de detección de cambios a menudo se construyen usando una combinación de análisis de vectores de cambio, clasificación de cambios y tal aporte experto.