3: La Fuerza Coriolis

Última actualización
Guardar como PDF

Page ID: 88545

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

La fuerza Coriolis es un elemento central de la dinámica de los flujos oceánicos y atmosféricos. En muchos libros de texto sobre mecánica clásica se da una derivación rigurosa usando cálculo vectorial, pero tales derivaciones a menudo no son la forma más efectiva de obtener una comprensión conceptual. Por lo tanto, proporcionaremos aquí una explicación cualitativa más intuitiva. A lo largo de este capítulo sobre Flujos Geofísicos, hemos estado hablando mucho de la 2da ley de Newton, pero la clave para entender la fuerza de Coriolis es más bien la 1ª ley de Newton: un objeto en movimiento permanece en movimiento con la misma velocidad y en la misma dirección a menos que actúe sobre él por un fuerza desequilibrada. La Tierra y todo lo que hay en ella se mueve constantemente, ya que la Tierra gira alrededor de su eje. Además, la dirección de todo este movimiento cambia constantemente: mientras estás escribiendo en tu escritorio a las 2 de la tarde, te estás moviendo en la dirección exacta opuesta respecto a cuando estabas acostado en tu cama a las 2 de la mañana Estos cambios forzados en la dirección del movimiento de los objetos que tienden a seguir moviéndose en el mismo dirección es lo que da lugar a las llamadas pseudo-fuerzas (que en realidad son muy reales, si por casualidad vives en un planeta giratorio como la Tierra).

La pseudo-fuerza que es la más fácil de entender conceptualmente es la fuerza centrífuga, representada a continuación.

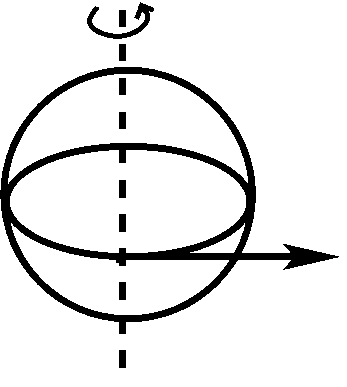
Esencialmente, los objetos tienden a ser arrojados de un cuerpo giratorio, porque los objetos siguen moviéndose en línea recta (como lo indica la flecha), mientras que la superficie del cuerpo giratorio no se mueve en línea recta (como lo indica el círculo). Afortunadamente, no necesitamos preocuparnos por ser arrojados de la Tierra, porque la fuerza gravitacional que mantiene nuestros pies en el suelo es aproximadamente 300 veces más fuerte que la fuerza centrífuga. La fuerza centrífuga no juega un papel significativo en la dinámica del océano y la atmósfera, pero sí hace que la Tierra sea ligeramente elíptica.

La fuerza Coriolis es una pseudo-fuerza que emerge cuando un objeto se mueve sobre la superficie de un cuerpo giratorio. La fuerza de Coriolis es conceptualmente mucho más sutil que la fuerza centrífuga y, de hecho, consiste en dos efectos diferentes, cada uno ilustrado a continuación:

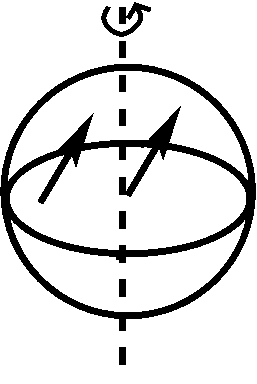
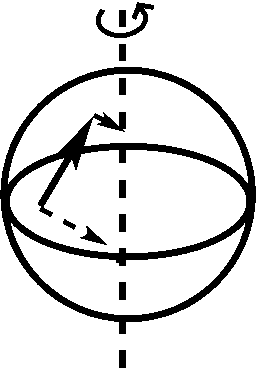
El panel izquierdo ilustra el primer efecto: un objeto que sigue moviéndose en la misma dirección en el espacio absoluto parece cambiar de dirección, ya que la Tierra gira hacia la derecha. Al principio, el objeto se mueve recto Norte hacia el polo (flecha izquierda), pero luego, la dirección del movimiento se convierte en Noreste en el marco de referencia de la Tierra (flecha derecha), aunque la dirección y velocidad del objeto no hayan cambiado en el espacio absoluto. El panel derecho ilustra el segundo efecto: a medida que un objeto se mueve sobre la superficie de la Tierra (como lo indica la flecha sólida), lleva consigo la velocidad de rotación de la Tierra (flechas discontinuas). A medida que el objeto se mueve hacia el Norte, entra en regiones donde la velocidad de rotación de la Tierra es menor que en su ubicación original. Así, tendrá un exceso de velocidad hacia el Este que desvía el movimiento del Norte hacia el Noreste, cuando se ve en el marco de referencia de la Tierra. En el marco de referencia de la Tierra, cada uno de estos 2 efectos conduce a una aceleración con una magnitud igual a\(\Omega * v \sin\theta \) (con\(\Omega \) la velocidad angular de\(v\) la Tierra, la velocidad del objeto en el marco de referencia terrestre y\(\theta\) la latitud), por lo que la aceleración total suma a \(2 * \Omega * v \sin\theta\)o\(f * v\), con el parámetro Coriolis\(f = 2 * \Omega * \sin\theta\). La fuerza Coriolis se encuentra en\(90^{\circ}\) ángulo con respecto al movimiento del objeto, a la derecha en el hemisferio norte, a la izquierda en el hemisferio sur; desaparece en el Ecuador (\(\theta=0\)). En las direcciones zonal y meridional, las aceleraciones ascienden a:

\[\dfrac{du}{dt}=f * v \]

\[\dfrac{dv}{dt}=-f * u\]

Aquí se demuestra el impacto de la fuerza de Coriolis en parcelas móviles de aire (o agua).