1.12: Comprender los mapas
- Page ID
- 89971
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Comprensión de los mapas
Los mapas son quizás las herramientas más importantes para la navegación y evaluación de características en la superficie terrestre, bajo el agua o incluso bajo tierra. Los mapas se utilizan para muchos temas relacionados con el uso del suelo y el manejo de los recursos naturales Los mapas se han utilizado en tiempos prehistóricos. Sin embargo, la evolución de los mapas en el mundo digital moderno ha cambiado la creación de mapas, mejorando su uso en casi todos los aspectos de la ciencia, la tecnología y la cultura modernas. Los mapas modernos se crean con sistemas de información geográfica (SIG). Un SIG es un programa de generación de mapas basado en computadora que puede fusionar información geográfica (espacial) con muchos tipos de temas tópicos en formato de base de datos. Dichos temas pueden consistir en información médica (como datos de brotes de enfermedades), recursos hídricos, carreteras, edificios e infraestructura cívica, información de la red eléctrica, información agrícola y biológica, etc.). Los datos satelitales se utilizan cada vez más para casi todos los aspectos del mapeo de la tierra, los océanos y los patrones climáticos.
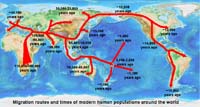
Figura 1.29. Los mapas muestran información temática en un contexto geográfico. El tema de este mapa muestra las rutas de migración humana en una base de mapa mundial.
Muchos mapas muestran información de relieve o elevación. El relieve se relaciona con las características de altura y forma de un paisaje (como relieve alto, bajo, relieve, relieve suave, relieve rugoso, etc. Los mapas de relieve sombreado muestran cambios en la elevación (topografía y batimetría) usando tonos de gris o color.
¿Qué son Latitud y Longitud?
Las ubicaciones en la superficie de la Tierra se definen mediante el sistema de coordenadas de latitud y longitud (Figura 1.30).
La latitud es la distancia angular de un lugar al norte o al sur del ecuador terrestre, generalmente expresada en grados y minutos. Las líneas de latitud se llaman paralelismos. Las líneas de latitud son paralelas al Ecuador. Cada grado de latitud está aproximadamente a 69 millas (111 kilómetros) de distancia. La latitud en el hemisferio norte se puede determinar avistando en la Estrella Norte (que se encuentra directamente sobre el Polo Norte) y determinando el ángulo de la estrella sobre el horizonte (restarla de 90°).
La longitud es la distancia angular de un lugar al este o al oeste del Meridiano Prime generalmente expresada en grados y minutos. Con el fin de hacer un mapa preciso de las estrellas para su uso en la navegación de barcos, en 1884, se designó una ubicación que indicaba la ubicación precisa de 0° Este-Oeste en la cruz de un telescopio en el Observatorio Real (ahora ubicado en los terrenos del Museo Marítimo Nacional) en Greenwich Inglaterra. Esta línea marca la ubicación de referencia del Prime Meridian que ahora se utiliza en todos los mapas globales (incluidos los sistemas de localización GPS). La Línea Internacional de Fecha se encuentra en el lado opuesto de la tierra ubicada 180° al este o al oeste del Meridiano Prime.
Un meridiano es un círculo de longitud constante que pasa por un lugar determinado en la superficie terrestre y los polos terrestres. Las líneas de longitud (de igual espaciado medido en grados) están ampliamente espaciadas en el ecuador pero convergen en un punto en los polos Norte y Sur. El Meridiano Prime se designa 0° (cero grados). Las líneas meridianas al este del Meridiano Principal se designan valores positivos (0° a 180° este); mientras que las líneas meridianas al oeste del Meridiano Prime se designan valores negativos (-0° a -180°). A 180° este u oeste se encuentra la Línea Internacional de Fecha. El grado de longitud es más ancho en el ecuador a 69.172 millas (111.321) y gradualmente se reduce a cero en los polos. A 40° norte o sur la distancia entre un grado de longitud es de 53 millas (85 km).
Definir ubicaciones con un sistema de coordenadas de latitud-longitud: cualquier ubicación en la superficie del planeta se puede definir por un número en grados, minutos y segundos al norte o al sur del Ecuador y al este u oeste del Meridiano Principal. (¡Compare con horas, minutos, segundos en un reloj!)
Figura 1.31. Mapa del mundo con latitud y longitud en una proyección de Mercator (plana)
Figura 1.32. Mapa del mundo que se muestra con Proyección Mercator - nota distorsión en latitudes altas porque las líneas de longitud no convergen
Figura 1.33. Mapa de América del Norte con Proyección Cónica Lambert - en esta escala la distorsión de América es mínima, pero mira América del Sur.
Ejemplo: Ubicación de la Estatua de la Libertad en
el Puerto de Nueva York Las coordenadas estándar (en grados, minutos y segundos) de la Estatua de la Libertad son:
Latitud: 40°68′92"N
Longitud: 74°04′ 45"W.
Descritas en grados decimales las coordenadas de la Estatua de la Libertad son:
Latitud: 40.689758° N
Longitud: - 74.045138° W.
Un ejemplo de San Diego, California
El monumento en lo alto del Monte Soledad en La Jolla se encuentra:
Latitud: 32.8398° N
Longitud: 117.2523° W.
Encuentre la latitud y longitud de cualquier ubicación o característica de paisaje con nombre en el sitio web de GeoNames.
La tierra es redonda (una esfera como un globo) pero los mapas son planos. Como resultado, los mapas que muestran grandes regiones se distorsionan. Las proyecciones de mapas son intentos de retratar una porción de la Tierra sobre una superficie plana (los ejemplos se muestran en las Figuras 1-31 a 1-33). El aplanamiento de un mapa siempre provoca algunas distorsiones de distancia, dirección, escala y área. Los mapas a gran escala (como un mapa de un continente o un mundo muestran mucha distorsión, sin embargo, los mapas a escalas pequeñas (como un mapa de una ciudad o barrio) tienen relativamente poca distorsión. Hay muchos sistemas de proyección de mapas, cada uno sirve para diferentes propósitos y tiene cierta variedad de distorsión. Conoce más sobre las proyecciones de mapas en el sitio web de Proyecciones de mapas del Servicio Geológico de Estados Unidos
Un Sistema de Posicionamiento Global (GPS) es un sistema satelital de navegación global basado en el espacio que proporciona información confiable de ubicación y hora en todo clima y en todo momento y en cualquier lugar en o cerca de la Tierra cuando y donde haya una línea de visión sin obstáculos a cuatro o más satélites GPS (Figura 1.35). El GPS ahora se utiliza para casi todas las formas de navegación de mapas digitales.