3.2: Flujo más allá de una esfera con números bajos de Reynolds

Haremos un inicio en los patrones de flujo y las fuerzas de fluido asociadas con el flujo de un fluido viscoso más allá de una esfera restringiendo la consideración a números bajos de Reynolds\(\rho U D / \mu\) (donde, como antes,\(U\) es la velocidad de aproximación uniforme y\(D\) es el diámetro de la esfera).

Figura\(\PageIndex{1}\): Flujo constante de un fluido viscoso a números de Reynolds muy bajos (“flujo rastrero”) más allá de una esfera. Las líneas de flujo se muestran en una sección plana paralela a la dirección del flujo y pasando por el centro de la esfera.

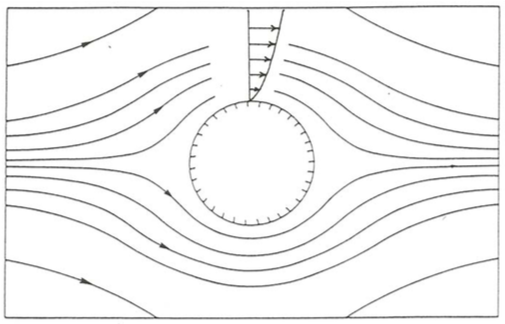
A números de Reynolds muy bajos,\(\mathrm{Re} \ll 1\), las líneas de flujo relativas a la esfera son aproximadamente como se muestra en la Figura\(\PageIndex{1}\). Lo primero a tener en cuenta es que para estos números muy pequeños de Reynolds el patrón de flujo es simétrico de adelante hacia atrás. Las líneas de flujo son rectas y uniformes en el arroyo libre muy al frente de la esfera, pero son desviadas a medida que pasan alrededor de la esfera. Para una gran distancia de la esfera, las líneas de flujo se encuentran algo más espaciadas, lo que indica que la velocidad del fluido es menor que la velocidad de flujo libre. ¿Eso daña tu intuición? Uno podría haber adivinado que las líneas de flujo estarían más abarrotadas alrededor de la sección media de la esfera, reflejando en su lugar una mayor velocidad, y como se mostrará más adelante en este capítulo, ese es el caso de números de Reynolds mucho más altos. (Vea una sección posterior para obtener más información sobre lo que casualmente he llamado líneas de flujo aquí). Para números muy bajos de Reynolds, sin embargo, el efecto del “hacinamiento”, que actúa para aumentar la velocidad, está más que compensado por el efecto del retraso viscoso, que actúa para disminuir la velocidad.

La velocidad del fluido es cero en todas partes en la superficie de la esfera (recuerde la condición de antideslizante) y aumenta solo lentamente alejándose de la esfera, incluso en las proximidades de la sección media: a números bajos de Reynolds, el efecto retardador de la esfera se siente por grandes distancias hacia el interior del fluido. Verás más adelante en este capítulo que la zona de retraso se contrae mucho a medida que aumenta el número de Reynolds, y el efecto de “hacinamiento” hace que la velocidad alrededor de la sección media de la esfera sea mayor que la velocidad de flujo libre excepto muy cerca de la superficie de la esfera; más sobre eso más adelante.

Figura\(\PageIndex{2}\): Coordenadas para la descripción de la distribución teórica de la velocidad en flujo pasado una esfera a números de Reynolds muy bajos (flujo rastrero).

Uso de la ecuación de Navier-Stokes para describir la velocidad y la presión de un flujo progresivo

Si quieres ver por ti mismo cómo varía la velocidad en las proximidades de la esfera, las ecuaciones\ ref {3.1} dan la distribución teórica de la velocidad\(v\), en función de la distancia\(r\) desde el centro de la esfera y el ángulo\(\theta\) medido alrededor de la esfera desde\(0^{\circ}\) at el punto delantero\(180^{\circ}\) al punto trasero (Figura\(\PageIndex{2}\)):

\[\begin{array}{l}{u_{r}=-U \cos \theta\left(1-\frac{3 R}{2 r}+\frac{R^{3}}{2 r^{3}}\right)} \\ {u \theta=U \sin \theta\left(1-\frac{3 R}{4 r}-\frac{R^{3}}{4 r^{3}}\right)}\end{array} \label{3.1}\]

Este resultado fue obtenido por Stokes (1851) especializando las ecuaciones Navier—Stokes para un flujo que se aproxima tan lento que las aceleraciones del fluido a medida que pasa alrededor de la esfera pueden ignorarse, dando como resultado una ecuación que puede resolverse analíticamente. Dije en el Capítulo 2 que la densidad del fluido\(\rho\) es necesaria como variable para describir la fuerza de arrastre sobre una esfera porque las aceleraciones se producen en el fluido a medida que la esfera se mueve a través de ella. Sin embargo, si estas aceleraciones son lo suficientemente pequeñas, es razonable esperar que se pueda descuidar su efecto sobre el flujo y las fuerzas. Los flujos de este tipo son pintorescos llamados flujos rastreros. La razón, a la que aludí en la sección anterior, es que en las ecuaciones de Navier—Stokes el término para tasa de cambio de impulso se vuelve pequeño más rápido que los dos términos restantes, para las fuerzas viscosas y las fuerzas de presión, a medida que disminuye el número de Reynolds.

Se puede ver en Ecuaciones\ ref {3.1} que a medida que\(r \rightarrow \infty\) la velocidad se acerca a su magnitud y dirección de flujo libre. La\(1/r\) dependencia en los segundos términos entre paréntesis en los lados de la derecha de Ecuaciones\ ref {3.1} refleja la distancia apreciable lejos de la esfera se sienten los efectos del retraso viscoso. Un cálculo simple usando Ecuaciones\ ref {3.1} muestra que, a una distancia igual al diámetro de la esfera desde la superficie de la esfera en la sección media en la dirección normal al flujo de corriente libre, la velocidad sigue siendo solo\(50 \%\) del valor de flujo libre.

En cada punto de la superficie de la esfera hay un valor definido de presión de fluido (fuerza normal por unidad de área) y de esfuerzo cortante viscoso (fuerza tangencial por unidad de área). Estos valores también provienen de la solución de Stokes para el flujo progresivo alrededor de una esfera. Para el esfuerzo cortante, podría usar Ecuaciones\ ref {3.1} para encontrar el gradiente de velocidad en la superficie de la esfera y luego usar la Ecuación 1.3.7 para encontrar el esfuerzo cortante. Para la presión, Stokes encontró una ecuación separada,

\[p-p_{0}=\frac{3}{2} \frac{\mu U R}{r^{2}} \cos \theta \label{3.2} \]

donde\(p_{0}\) está la presión de corriente libre. Cifras\(\PageIndex{3}\) y\(\PageIndex{4}\) dar una idea de la distribución de estas fuerzas. Es fácil entender por qué el esfuerzo cortante viscoso debe ser mayor alrededor de la sección media y menos en la superficie frontal y posterior de la esfera, porque ahí es donde la velocidad cerca de la superficie de la esfera es mayor. La distribución de la presión, alta en la parte delantera y baja en la parte posterior, también tiene sentido intuitivo. Sin embargo, es interesante que existe una gran diferencia de presión de adelante hacia atrás a pesar de la simetría casi perfecta de adelante hacia atrás del flujo.

Figura\(\PageIndex{3}\): Distribución del esfuerzo cortante en la superficie de una esfera en un flujo de fluido viscoso a muy bajos números de Reynolds (flujo rastrero). La distribución se muestra en una sección plana paralela a la dirección del flujo y pasando por el centro de la esfera.

Figura\(\PageIndex{4}\): Distribución de la presión sobre la superficie de una esfera en un flujo de fluido viscoso a muy bajo número de Reynolds (flujo rastrero). La distribución se muestra en una sección plana paralela a la dirección del flujo y pasando por el centro de la esfera.

Uso de la ecuación de Navier-Stokes para describir la fuerza de arrastre (Ley de Stoke)

Se puede imaginar sumar tanto presiones como esfuerzos de cizallamiento viscosos en toda la superficie, recordando que se debe tener en cuenta tanto la magnitud como la dirección, para obtener una fuerza de presión resultante y una fuerza viscosa resultante sobre la esfera. Debido a la simetría del flujo, ambas fuerzas resultantes se dirigen directamente aguas abajo. Luego puede agregarlos juntos para obtener una gran resultante, la fuerza de arrastre total\(F_{D}\). Usando las soluciones para velocidad y presión dadas anteriormente (Ecuaciones\ ref {3.1} y\ ref {3.2}), Stokes obtuvo el resultado

\[F_{D}=6 \pi \mu U R \label{3.3} \]

para la fuerza de arrastre total sobre la esfera. La densidad no aparece en la ley de Stokes porque entra en la ecuación del movimiento solo el término masa-aceleración del tiempo, el cual fue descuidado. Para los números de Reynolds menores que aproximadamente uno, el resultado expresado por la Ecuación\ ref {3.3} (llamada ley de Stokes) está casi en perfecto acuerdo con el experimento. Resulta que en el rango Stokes, pues\(Re \ll 1\), exactamente un tercio de\(F_{D}\) se debe a la fuerza de presión y dos tercios se debe a la fuerza viscosa.

Ahora finge que no sabes nada de la ley de Stokes por el arrastre en una esfera a números muy bajos de Reynolds. Si razonas, como se discutió anteriormente, eso se\(\rho\) puede omitir de manera segura de la lista de variables que influyen en la fuerza de arrastre, entonces te quedan cuatro variables:\(F_{D}\),\(U\),\(D\), y\(\mu\). La relación funcional entre estas cuatro variables es necesariamente

\[f\left(F_{D}, U, D, \mu\right)= \text{const} \label{3.4} \]

Solo se puede formar una variable adimensional de las cuatro variables\(F_{D}\),,\(U\)\(D\), y\(\mu\), a saber\(F_{D} / \mu U D\). Entonces, en forma adimensional, la relación funcional en la Ecuación\ ref {3.4} se convierte

\[\frac{F_{D}}{\mu U D}= \text{const} \label{3.5} \]

Se puede pensar en la Ecuación\ ref {3.5} como un caso especial de la Ecuación 2.3.1. Si masajea la ley de Stokes (Ecuación\ ref {3.3}) solo un poco, dividiendo ambos lados de la ecuación por\(\mu U R\) para hacer que la ecuación sea adimensional, y usando el diámetro\(D\) en lugar del radio\(R\), obtienes

\[\frac{F_{D}}{\mu U D}=3 \pi \label{3.6} \]

Compare esto con la Ecuación\ ref {3.5} anterior. Se ve que el análisis dimensional por sí solo, sin recurrir a intentar soluciones exactas, proporciona la ecuación dentro de la constante de proporcionalidad. La teoría de Stokes proporciona el valor de la constante.

El patrón de flujo alrededor de la esfera y las fuerzas fluidas que actúan sobre la esfera se vuelven gradualmente diferentes a medida que aumenta el número de Reynolds. Los cambios progresivos en el patrón de flujo con el aumento del número de Reynolds se discuten con más detalle más adelante en este capítulo, después de bastantes antecedentes necesarios en los fundamentos de la dinámica de fluidos.