3.6: Silogismos categóricos

Como hemos dicho, la lógica aristotélica se limita a evaluar argumentos cuyas proposiciones —premisas y conclusión—son categóricas. Existe una restricción adicional: la Lógica Aristotélica sólo evalúa los silogismos categóricos. Se trata de un tipo especial de argumento, que reúne las siguientes condiciones:

Un silogismo categórico es un argumento deductivo que consta de tres proposiciones categóricas (dos premisas y una conclusión); colectivamente, estas tres proposiciones presentan exactamente tres clases; cada una de las tres clases ocurre exactamente en dos de las proposiciones.

Eso es un bocado, pero un ejemplo lo dejará claro. Aquí hay un silogismo categórico (tonto):

Todas las ardillas son republicanas.
Algunos republicanos son golfistas.
Por lo tanto, algunas ardillas son golfistas.

Este argumento cumple con las condiciones de la definición: tiene tres proposiciones; hay exactamente tres clases involucradas (ardillas, republicanos y golfistas); y cada una de las tres clases ocurre exactamente en dos de las proposiciones (verifíquelo y vea).

Existe una terminología especial para los términos y premisas de clase en los silogismos categóricos. Cada uno de los tres términos de clase tiene una designación especial. El llamado término mayor es el término que aparece en posición predicada en la conclusión; en nuestro tonto ejemplo, ese es 'golfistas'. El término menor es el término que aparece en posición sujeto en la conclusión; en nuestro ejemplo, eso es 'ardillas'. El término medio es el otro, el que aparece en cada una de las premisas; en nuestro ejemplo, se trata de 'republicanos'.

Los locales también tienen designaciones especiales. La premisa principal es la que tiene el término mayor en ella; en nuestro ejemplo, eso es 'Algunos republicanos son golfistas'. La premisa menor es la otra, la que presenta el término menor; en nuestro ejemplo, es 'Todas las ardillas son republicanas'.

Restricción final: los silogismos categóricos deben escribirse en forma estándar. Esto significa enumerar los locales en el orden correcto, con la premisa mayor primero y la premisa menor en segundo lugar. Si miras nuestro tonto ejemplo, notarás que no está en forma estándar. Para solucionarlo, necesitamos revertir el orden de las premisas:

Algunos republicanos son golfistas.
Todas las ardillas son republicanas.
Por lo tanto, Algunas ardillas son golfistas.

Una vieja preocupación puede surgir de nuevo en este punto: al restringirse a una clase tan limitada de argumentos, ¿no corre el riesgo de no poder evaluar muchos argumentos de la vida real que nos importan? La respuesta a esta preocupación sigue siendo la misma: si bien la mayoría (casi todos) de los argumentos de la vida real no se presentan como silogismos categóricos de forma estándar, un número sorprendente de ellos puede traducirse en esa forma. Los argumentos con más de dos premisas, por ejemplo, se pueden reescribir como cadenas de subargumentos de dos premisa. Como fue el caso cuando planteamos esta preocupación antes, dejaremos de lado los detalles desordenados de exactamente cómo se logra esto en casos particulares.

Forma lógica

Como dijimos al inicio de nuestra exploración de la lógica deductiva, hay tres cosas que tal lógica debe hacer: (1) domar el lenguaje natural; (2) definir con precisión la forma lógica; y (3) desarrollar una manera de probar formas lógicas para su validez. Hasta ahora, nos ha preocupado el primer paso. Es (finalmente) momento de pasar a la segunda y tercera.

La forma lógica de un silogismo categórico está determinada por dos rasgos del argumento: su estado de ánimo y su figura. Primero, el estado de ánimo. El estado de ánimo de un silogismo está determinado por los tipos de proposiciones categóricas contenidas en el argumento, y el orden en que ocurren. Para determinar el estado de ánimo, ponga el argumento en forma estándar, y luego simplemente enumere los tipos de categorías (A, E, I, O) que aparecen en el orden en que ocurren. Hagamos esto con nuestro tonto ejemplo:

Algunos republicanos son golfistas.
Todas las ardillas son republicanas.
Por lo tanto, algunas ardillas son golfistas.

De arriba a abajo, tenemos una I, una A y una I. Entonces el ánimo de nuestro argumento es IAI. Así de fácil. Resulta que hay 64 estados de ánimo posibles: 64 formas de combinar A, E, I y O en combinaciones únicas de tres letras, desde AAA hasta OOO y todo lo demás.

El otro aspecto de la forma lógica es la figura del argumento. La figura de un silogismo categórico está determinada por la disposición de sus términos. Dadas las restricciones de nuestra definición, existen cuatro posibilidades diferentes para los silogismos de forma estándar. Los enumeraremos esquemáticamente, usando estas convenciones: dejemos que 'S' signifique el término menor, 'P' significa el término mayor y 'M' significa el término medio. Aquí están las cuatro cifras:

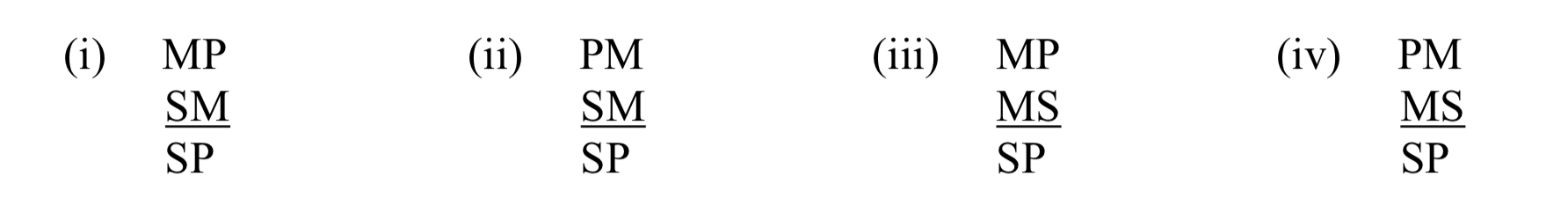
Nuevamente, lo único que determina la figura es la disposición de los términos, ya sea que aparezcan en posición de sujeto o predicado en sus premisas. En nuestros esquemas, que la letra esté listada primero indica que el término aparece en posición de sujeto; que aparezca segundo indica que está en posición de predicado. Entonces, en la primera figura, en la premisa mayor (la primera), el término medio (M) está en posición de sujeto y el término mayor (P) está en posición predicado. Observe que para las cuatro cifras, el sujeto y predicado de la conclusión sigue siendo el mismo: esto se debe a que, por definición, el término menor (S) es el sujeto de la conclusión y el término mayor (P) su predicado.

Volviendo a nuestro tonto ejemplo, podemos determinar su figura:

Algunos republicanos son golfistas.
Todas las ardillas son republicanas.
Por lo tanto, algunas ardillas son golfistas.

Quizás lo más fácil de hacer es enfocarse en el mediano plazo, el que aparece en cada uno de los locales —en este caso, los 'republicanos'. Ocurre en posición de sujeto en la premisa mayor, luego posición predicada en la premisa menor. Escaneando las cuatro figuras, solo busco la que tiene 'M' listada en primera posición en la parte superior, luego segunda posición en el centro. Esa es la primera cifra.

Entonces el ánimo de nuestro argumento de muestra es IAI, y está en la primera figura. La forma lógica es solo el estado de ánimo y la figura, y convencionalmente, enumeramos formas lógicas como esta: IAI-1 (el estado de ánimo, un guión, luego un número entre 1 y 4 para la figura).

Hay 4 figuras y 64 estados de ánimo. Eso nos da 256 posibles formas lógicas. Resulta que sólo 15 de estos son válidos. Necesitamos una forma de probarlos. Es a esa tarea a la que nos dirigimos ahora.

Prueba de validez del diagrama de Venn

Para probar la validez de las formas silogísticas, se procede en tres pasos:

1. Dibuja tres círculos superpuestos, así:

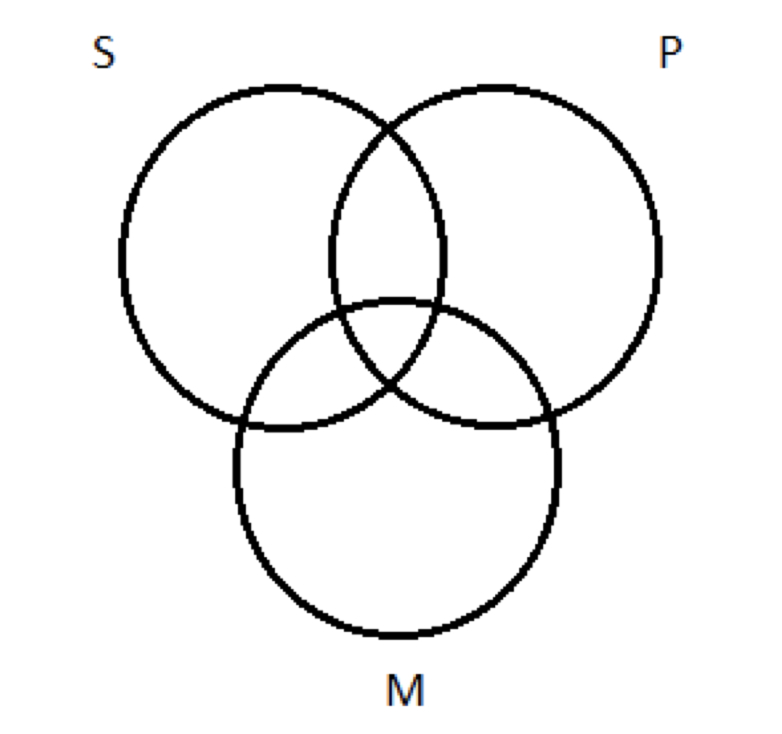
Eso nos da un círculo para cada uno de los tres términos del silogismo: menor (S), mayor (P) y medio (M).

2. Representar las aseveraciones hechas por las premisas del silogismo en este diagrama, utilizando el sombreado y Xs según corresponda, representando las proposiciones individuales A, E, I u O de la manera habitual:

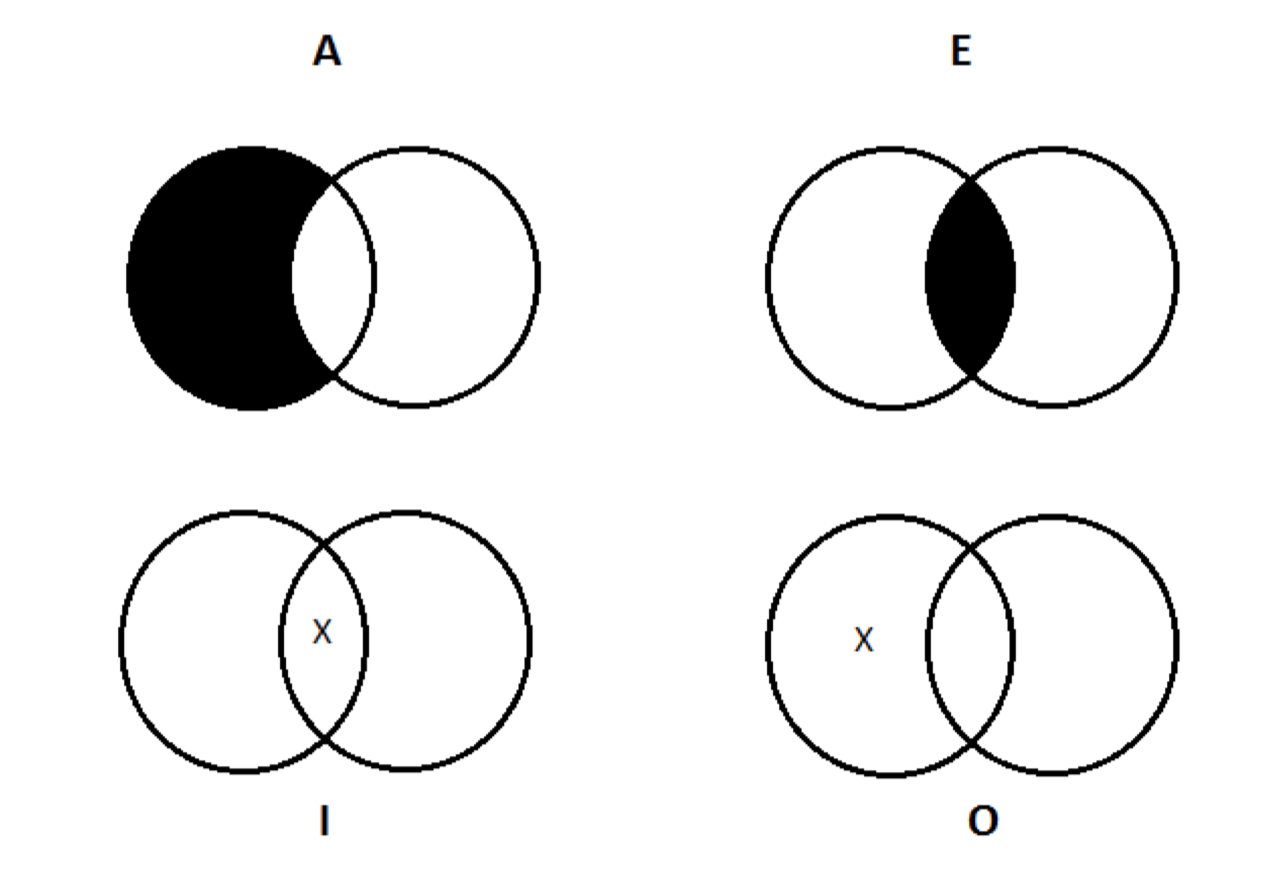
Cada una de las premisas será una proposición referente únicamente a dos de las tres clases (S, P y M). La premisa mayor se referirá a M y P (en algún orden); la premisa menor se referirá a M y S (en algún orden). La forma en que se etiquetarán los círculos (con S, M, P) dependerá de estos datos.

3. Después de que las premisas hayan sido representadas en el diagrama de tres círculos, miramos el producto terminado y preguntamos: “¿Esta imagen implica la verdad de la conclusión?” Si lo hace, el formulario es válido; si no lo hace, no es válido.

En el transcurso de la ejecución de la prueba, mantendremos dos cosas en mente: una regla general y una convención:

Regla de oro: En el paso 2, representar premisas universales (A y E) antes que particulares (I y O) (si hay elección).

Convención: En casos de indeterminación, dibujar Xs a ambos lados de las líneas fronterizas.

Tenemos que explicar a qué equivale la “indeterminación”; lo haremos en un momento. Por ahora, para que todo esto quede más claro, deberíamos repasar algunos ejemplos.

Empecemos por el inicio (alfa-numéricamente): AAA-1. Queremos probar la validez de esta forma silogística. ¿Qué aspecto tiene un argumento de esta forma, esquemáticamente? Bueno, sus tres proposiciones son afirmativas universales, así que son todas de la forma Todos __ son __. Contamos con:

Todos los __ son __
Todos los __ son __
Por lo tanto, todos los __ son __

Eso es lo que nos dice el estado de ánimo (AAA). Tenemos que averiguar cómo rellenar los espacios en blanco con S, P y M. La figura nos dice cómo hacerlo. AAA-1: entonces, primera figura. Eso se ve así:

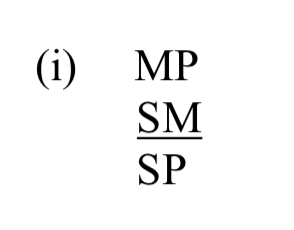
Así AAA-1 se puede representar esquemáticamente así:

Todas las M son P.
Todas las S son M.
Por lo tanto, todas las S son P.

Para probar la validez de este formulario, comenzamos con el paso 1, y dibujamos tres círculos:

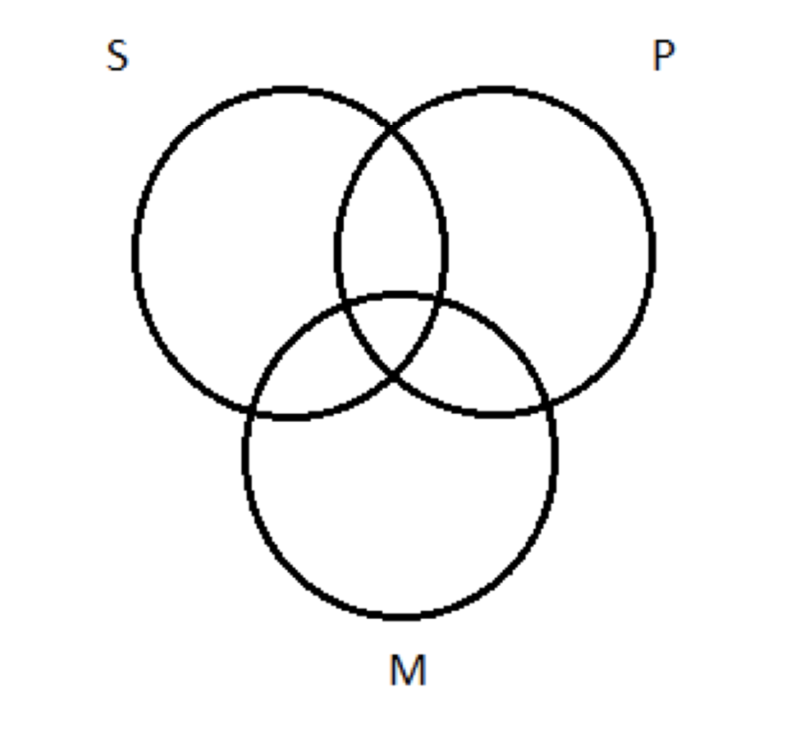
En el paso 2, representamos las premisas en este diagrama. (Se supone que debemos tener en cuenta la regla general de que, dada una opción, debemos representar premisas universales antes que las particulares, pero como ambas premisas son universales, esta regla no se aplica a este caso). Podemos comenzar con la premisa principal: Todas las M son P. En un diagrama regular de Venn de dos círculos, eso se vería así:

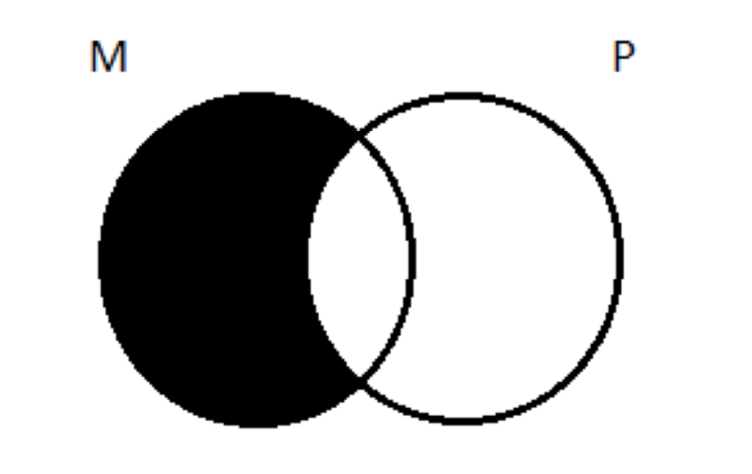
El truco es transferir este diagrama de dos círculos al uno de tres círculos. Al hacerlo, tenemos en cuenta que todas las partes de M que están fuera de P deben estar sombreadas. Eso nos da esto:

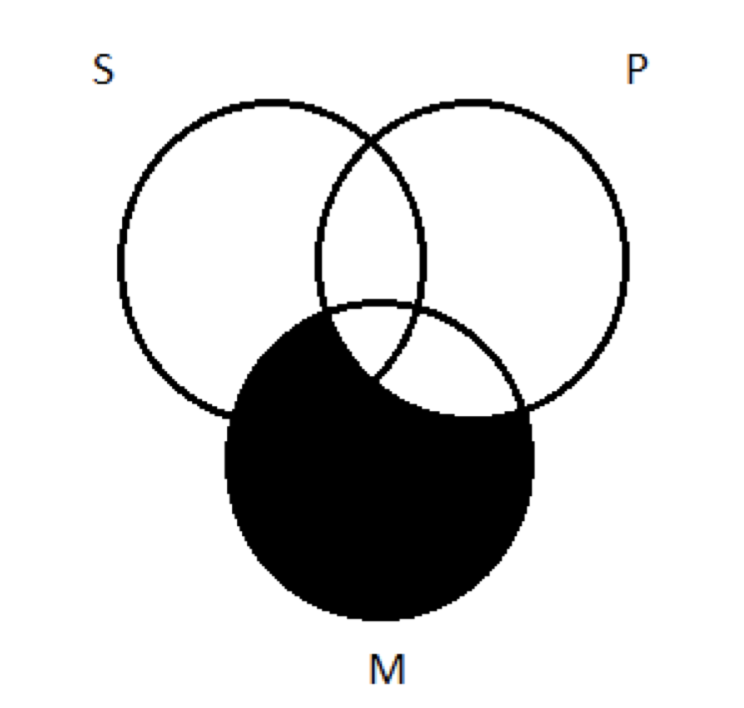
Tenga en cuenta que en el curso de sombrear las regiones necesarias de M, sombreamos parte de S. Eso está bien. Esos miembros de la clase S son Ms que no son Ps; no existe tal cosa, así que tienen que irse.

A continuación, representamos la premisa menor: Todas las S son M. Con dos círculos, eso se vería así:

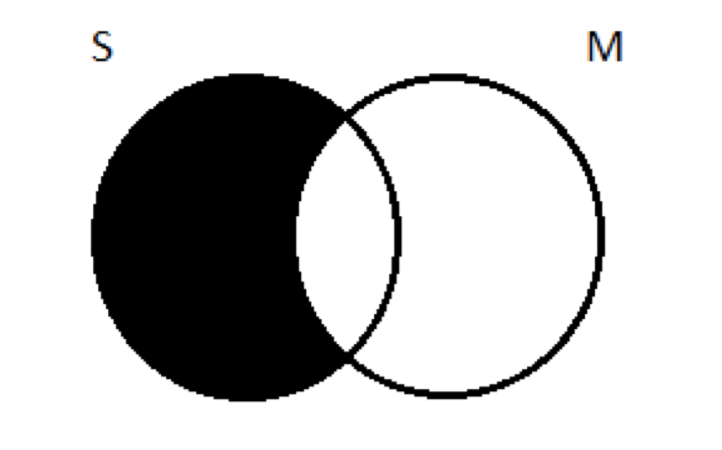
Transferir eso al diagrama de tres círculos significa sombrear todas las partes de S fuera de M:

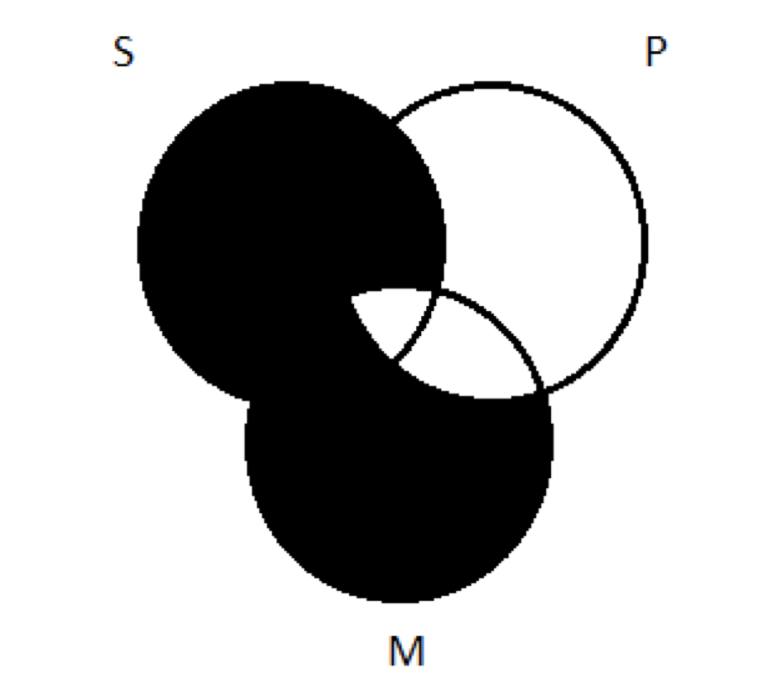
El paso 2 está completo: hemos representado las aseveraciones hechas por las premisas. En el paso 3 preguntamos si este diagrama garantiza la verdad de la conclusión. Bueno, nuestra conclusión es All S are P. En un diagrama de dos círculos, eso se ve así:

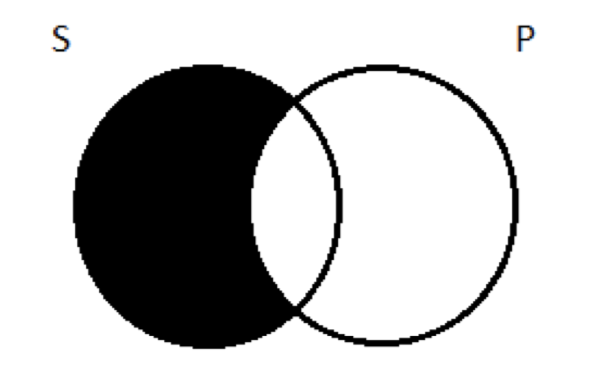
¿Nuestro diagrama de tres círculos garantiza la verdad de Todos los S son P? Centrándose en los círculos S y P, y comparando los dos diagramas, hay una pequeña diferencia: parte del área de superposición entre S y P está sombreada en nuestro diagrama de tres círculos, pero no está en la representación de dos círculos. Pero eso no afecta nuestro juicio sobre si el diagrama garantiza que Todas las S son P. Recuerden, esto puede pensarse como una afirmación de que cierto tipo de cosas no existe, una S que está fuera del círculo P. Si hay alguna Ss (y puede que no la haya), también serán Ps. Nuestro diagrama de tres círculos lo garantiza de hecho. No puede haber una S que no sea P; esas áreas están sombreadas. Cualquier S que encuentres también será una P; estará en esa pequeña región en el centro donde se superponen los tres círculos.

Entonces, como la respuesta a nuestra pregunta es “sí”, la forma silogística AAA-1 es válida. Dato trivial: a todas las formas silogísticas válidas se les dieron apodos mnemotécnicos en la Edad Media para ayudar a los estudiantes a recordarlas. AAA-1 se llama “Bárbara”. No realmente. Todas las letras del nombre tenían algún significado: las vocales indican el estado de ánimo (AAA); las otras letras representan rasgos de la forma que van más allá de nuestra breve investigación sobre la Lógica Aristotélica.

Debemos reflexionar por un momento sobre por qué funciona este método. Dibujamos una imagen que retrata las aseveraciones hechas por las premisas del argumento. Entonces nos preguntamos si ese panorama garantiza la conclusión. Esto debería sonar familiar. Estamos probando la validez, y por definición, un argumento es válido por si sus premisas garantizan su conclusión; es decir, SI las premisas son verdaderas, entonces la conclusión también debe ser cierta. Nuestro método refleja la definición. Cuando representamos las premisas en el diagrama de tres círculos, estamos dibujando una imagen de lo que parece para que las premisas sean ciertas. Entonces preguntamos, sobre esta imagen —que muestra un mundo en el que las premisas son ciertas— si nos obliga a aceptar la conclusión, si representa un mundo en el que la conclusión debe ser cierta. Si lo hace, el argumento es válido; si no es así, entonces no lo es El método se desprende directamente de la definición de validez.

Para ilustrar mejor el método, deberíamos hacer algunos ejemplos más. AII-3 es útil. El estado de ánimo nos dice que va a quedar así:

Todos los __ son __
Algunos __ son __
Por lo tanto, algunos __ son __

Y estamos en la tercera cifra:

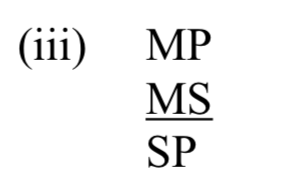
Entonces rellenamos los espacios en blanco para obtener el formulario esquemático:

Todas las M son P
Algunas M son S
Por lo tanto, algunas S son P

Comenzamos la prueba de este formulario con el diagrama de tres círculos en blanco:

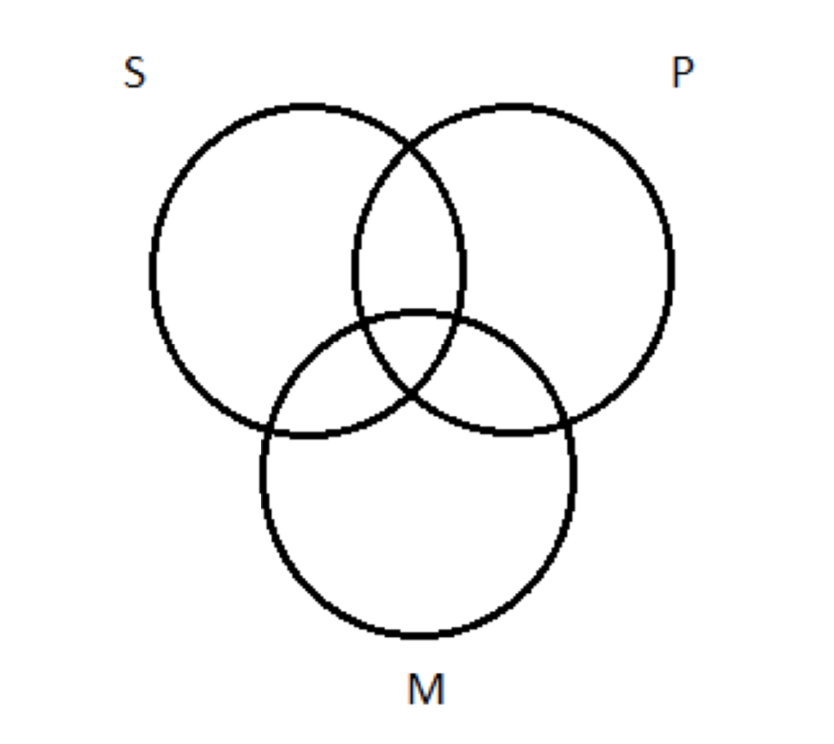
Paso 2: representar las premisas. Y aquí, se aplica nuestra regla general: representar los universales antes que los particulares. La premisa mayor es una proposición universal (A); la premisa menor es una particular (I). Entonces representamos primero la premisa principal. Eso es Todo M son P. Ya hicimos esto. Recordemos que Bárbara tiene la misma premisa principal. Así que representar eso en el diagrama nos da esto:

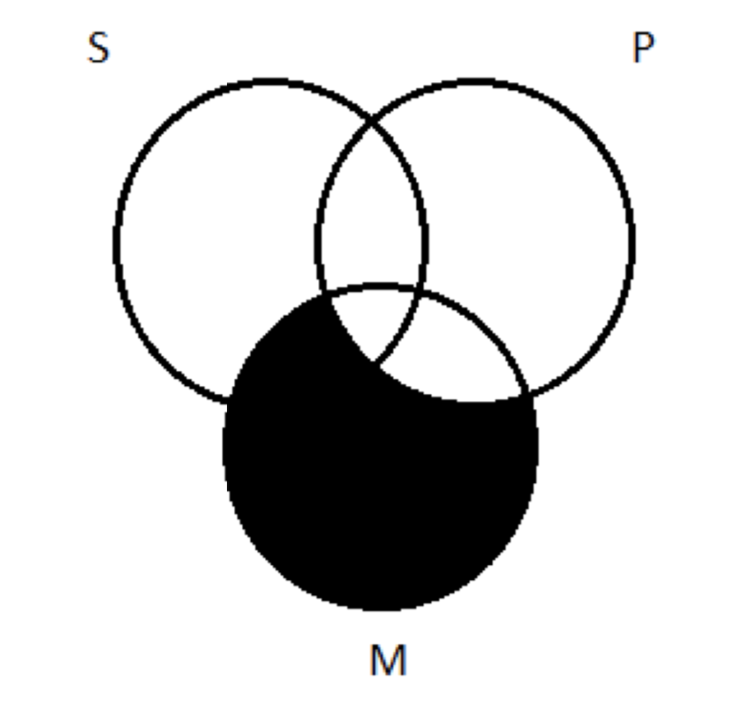
A continuación, la premisa menor: Algunas M son S. Recall, con proposiciones particulares, las representamos usando una X para indicar lo que se dice que existe. Esta proposición afirma que hay al menos una cosa que es tanto M como S:

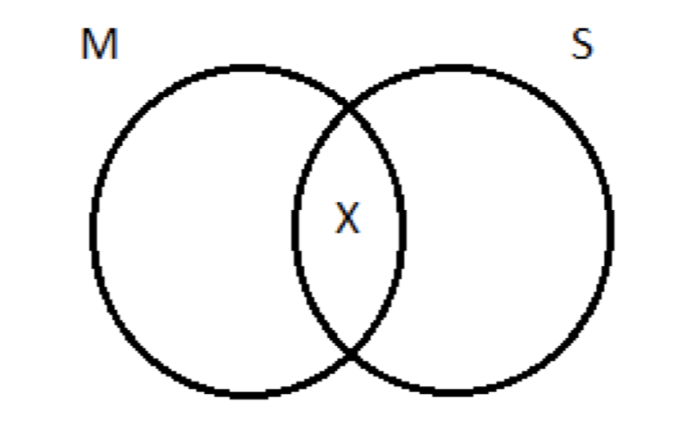
Tenemos que transferir esto al diagrama de tres círculos. Necesitamos una X que esté tanto en el círculo M como en el S. Si miramos el área de superposición entre ambos, vemos que parte de ella ha sido sombreada como resultado de representar la premisa principal, por lo que solo hay un lugar para que vaya la X:

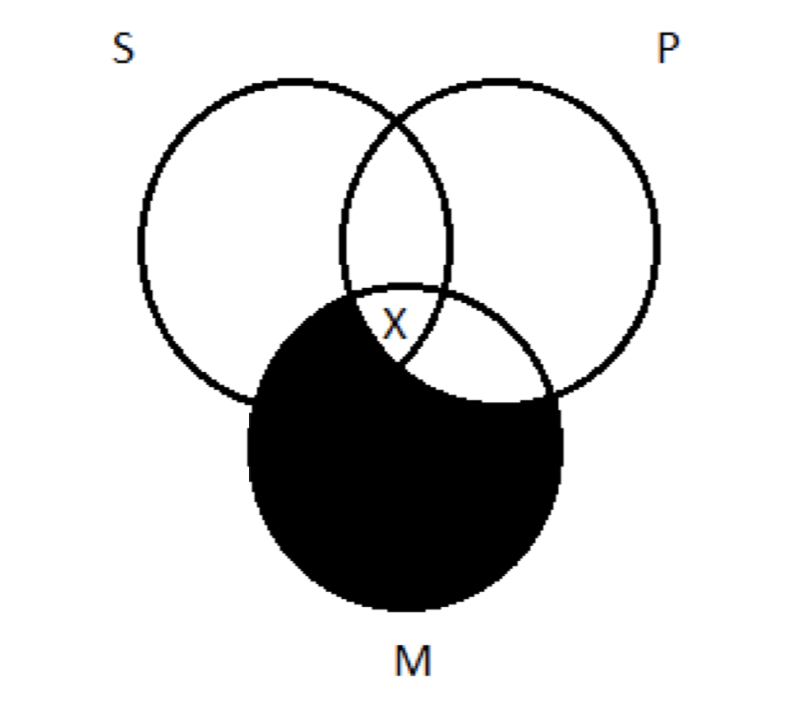
El paso 2 está completo: se representan las premisas. Entonces procedemos al paso 3 y preguntamos: “¿Esta imagen garantiza la conclusión?” La conclusión es Algunos S son P; eso es una aseveración de que hay al menos una cosa que es a la vez S y P. ¿Hay? ¡Sí! Esa X que dibujamos en el transcurso de representar la premisa menor está en el punto dulce, el área de superposición entre S y P. Garantiza la conclusión. El argumento es válido. (Si tienes curiosidad, su apodo mnemotécnico es 'Datisi'. Raro, lo sé; era la Edad Media.)

Ese es otro uso exitoso de la prueba del diagrama de Venn para la validez, pero quiero volver a revisar algo de ello. Quiero que reflexionemos sobre por qué tenemos la regla general para representar premisas universales antes que las particulares. Recuerden, teníamos la premisa mayor universal Todos los M son P y la premisa menor particular Algunos M son S. La regla general nos hizo representarlos en ese orden. ¿Por qué? ¿Qué hubiera pasado si hubiéramos hecho las cosas al revés? Habríamos comenzado con un diagrama de tres círculos en blanco y tuvimos que representar Algunos M son S en él. Eso significa una X en el área de superposición entre M y S. Esa área, sin embargo, se divide en dos subregiones (etiquetadas 'a' y 'b'):

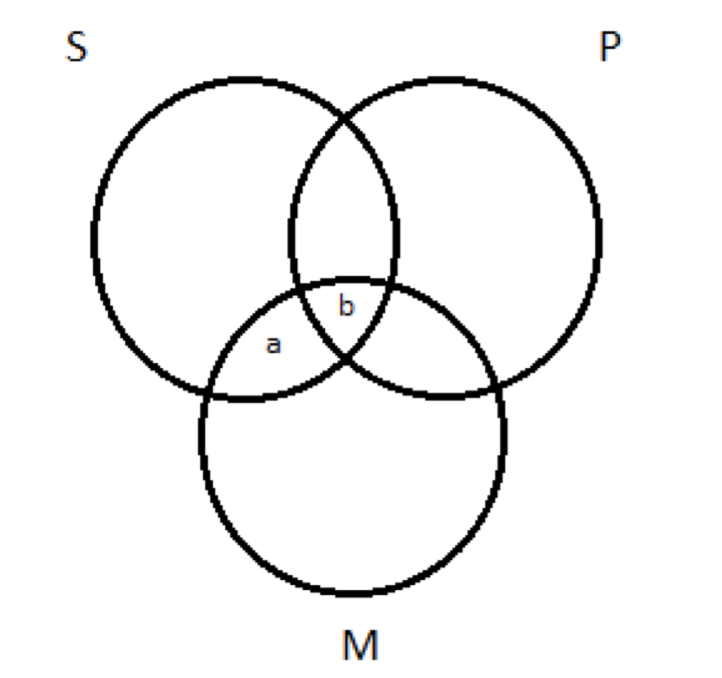
¿Dónde pongo mi X—en la región a o b? Observe, hace la diferencia: si pongo la X es región a, entonces está fuera del círculo P; si la pongo en la región b, entonces está dentro del círculo P. La pregunta es: “¿Es esto que dice la premisa menor existe una P o no una P?” Estoy representando una premisa que solo afirma Algunos M son S. Esa premisa no dice nada de P. Es silenciosa sobre nuestra pregunta; no nos da ninguna orientación sobre cómo elegir entre las regiones a y b. ¿Qué hacer? Este es uno de los casos de “indeterminación” que mencionamos antes cuando introdujimos una convención a tener en cuenta a la hora de ejecutar la prueba de validez: En casos de indeterminación, dibujar Xs a horcajadas sobre líneas límite. No tenemos forma de elegir entre las regiones a y b, así que cuando dibujamos nuestra X, dividimos la diferencia:

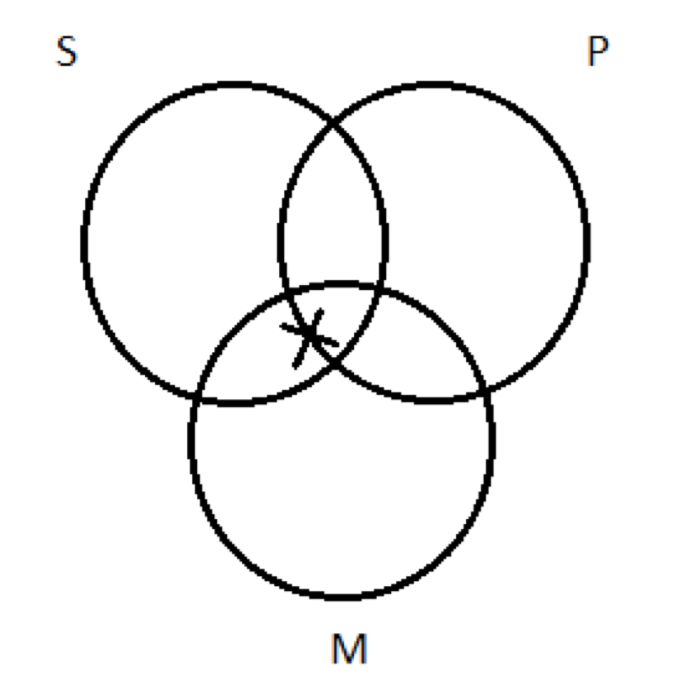
Este dibujo indica que hay una X ahí en alguna parte, ya sea dentro o fuera del círculo P, no sabemos cuál.

Y ahora vemos la razón de nuestra regla general: representar los universales antes que los particulares. Porque si procedemos a representar la premisa universal Todos los M son P, sombreamos así:

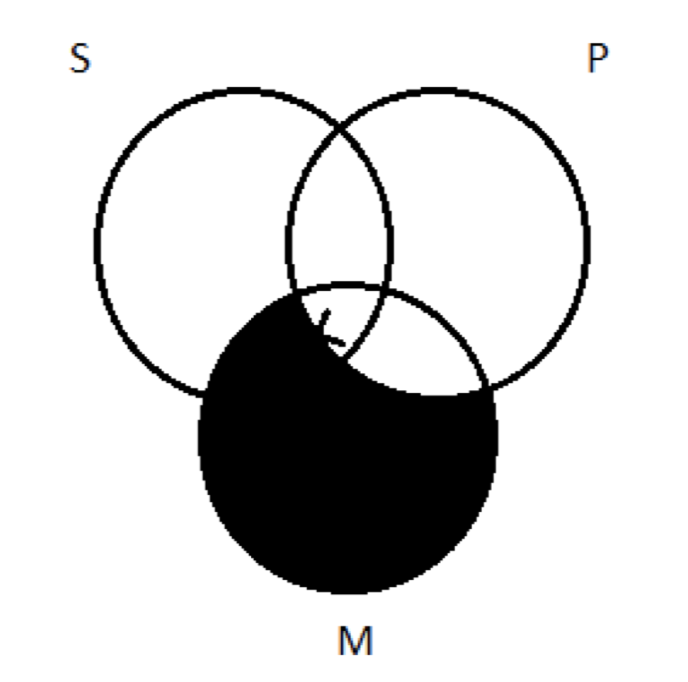
El sombreado borró la mitad de nuestra X. Es decir, resolvió nuestra cuestión de si la X debía ir o no en el círculo P: debería. Entonces ahora tenemos que retroceder un borrar el Half-an-X que queda y volver a dibujar la X en esa región central y terminar con el diagrama terminado al que llegamos antes:

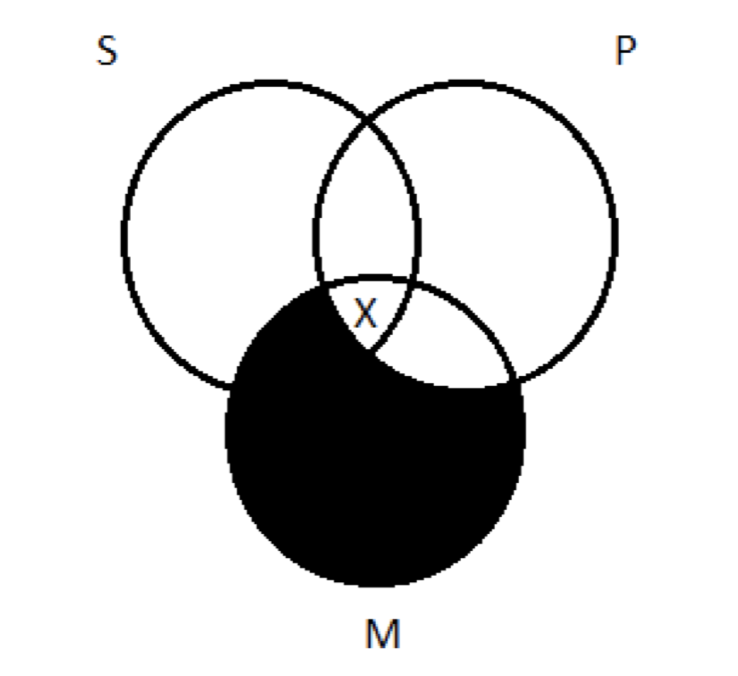
Nos hubiéramos ahorrado el problema si hubiéramos seguido la regla general para empezar y representar lo universal antes de lo particular, sombreando antes de la X. Esa es la utilidad de la regla: a veces elimina la indeterminación que de otro modo estaría presente.

Un ejemplo más para ilustrar cómo funciona este método. Probemos EOI-1. Señalando que en la primera figura el término medio es primero sujeto y luego predicado, podemos rellenar rápidamente el esquema:

No M son P
Algunas S no son M.
Por lo tanto, algunas S son P.

Siguiendo la regla general, describimos primero la premisa universal (E). No M are P afirma que no hay nada que esté en ambas clases. El área de superposición entre ellos está vacía. Con dos círculos, tenemos esto:

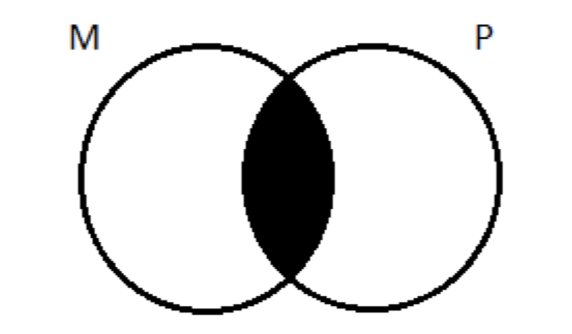
Al transferir esto al diagrama de tres círculos, sombreamos toda el área de superposición entre los círculos M y P (recortando parte de S en el camino):

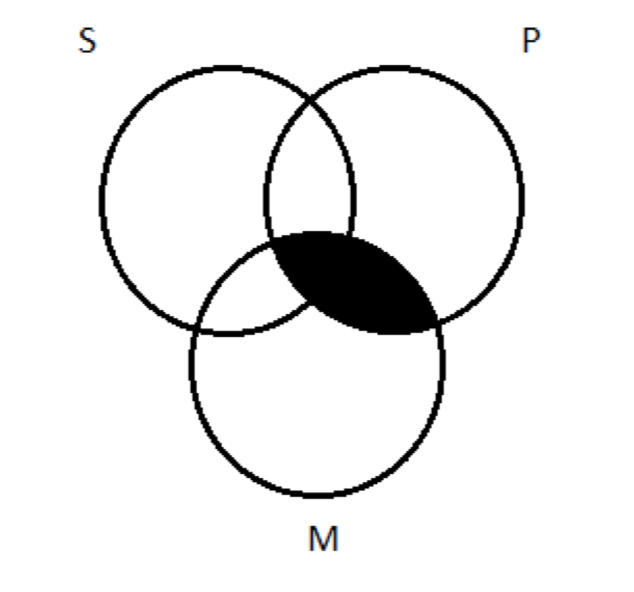
A continuación, la premisa particular (O): Algunas S no son M. Esto afirma la existencia de algo— es decir, una cosa que es una S pero no una M. Necesitamos una X en el círculo S que fuera del círculo M:

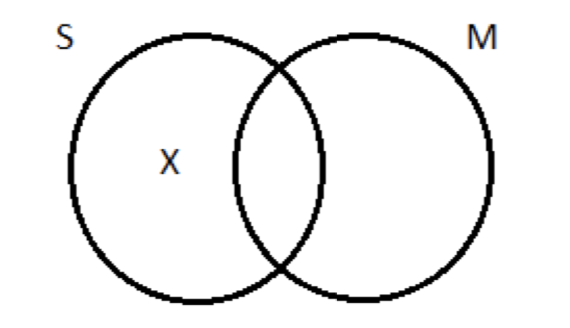
Pasando al diagrama de tres círculos, sin embargo, las cosas se ponen desordenadas. El área de S que está fuera de M se divide en dos subregiones (etiquetadas 'a' y 'b'):

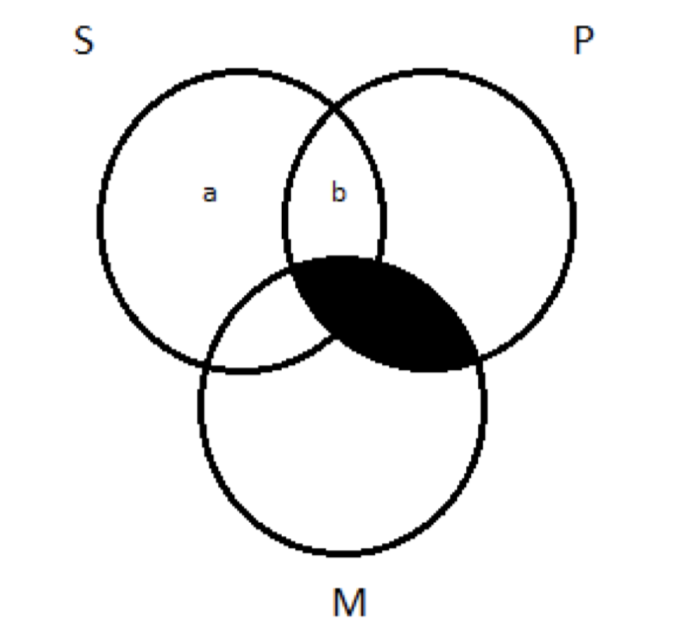
Necesitamos una X en algún lugar de ahí, pero ¿la ponemos en la región a o la región b? Hace la diferencia: si la ponemos en la región b, es una P; si la ponemos en la región a, no lo es. Este es el mismo problema que enfrentamos antes. Estamos representando una preestreno —algunas S no son M— eso guarda silencio sobre la cuestión de si la cosa es o no una P. Indeterminación. No podemos decidir entre a y b, así que dividimos la diferencia:

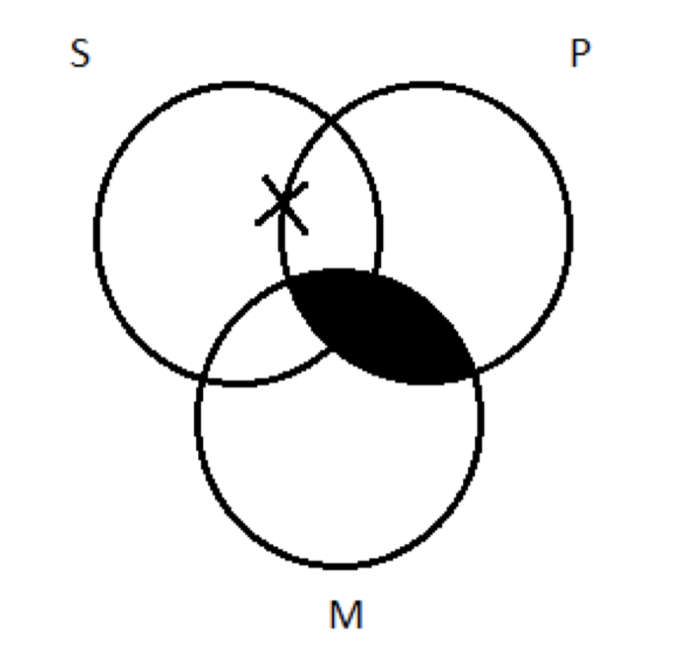
Esa X puede estar dentro de P, o puede que no; no lo sabemos. Este es un caso en el que seguimos la regla general, representando la premisa universal antes de la particular, pero no tuvo el beneficio que tenía cuando probamos AII-3: no quitó la indeterminación. Eso puede suceder. La regla general está en su lugar porque a veces elimina la indeterminación; aunque no siempre funciona.

Entonces ahora que hemos representado las premisas, nos preguntamos si garantizan la conclusión. ¿El mundo representado en nuestro diagrama es uno en el que la conclusión debe ser cierta? La conclusión es Algunos S son P: afirma que hay al menos una cosa que es a la vez S y P. ¿Nuestra imagen tiene tal cosa? Hay una X en la foto. ¿Se ajusta a la factura? ¿Es tanto S como P? Bueno, uh... ¿Tal vez? Esa X puede estar dentro del área de solapamiento entre S y P; entonces otra vez, puede que no lo sea.

Oy. ¿Qué decimos? Es tentador decir esto: no sabemos si el argumento es válido o no; depende de dónde esté realmente esa X. Pero esa no es la respuesta correcta. Recuerde, estamos probando la validez, para saber si las premisas garantizan o no la conclusión. Podemos responder a esa pregunta: ellos no, para una garantía, necesitaríamos una X en nuestra imagen que definitivamente está dentro de esa región media. No tenemos tal X. Estas premisas dejan abierta la posibilidad de que la conclusión sea cierta; no la descartan. Pero eso no es suficiente para la validez. Para que un argumento sea válido, las premisas deben requerir la conclusión, obligarla a nosotros. Estos no. El formulario EOI- 1 no es válido. (Triste pero cierto: las formas silogísticas inválidas no tienen apodos mnemotécnicos.)

Ejercicios

1. Identificar la forma lógica de los siguientes argumentos.

(a) Debido a que algunos wisconsinitas son criminales y todos los criminales son sinvergüenzas, se deduce que algunos sinvergüenzas son wisconsinitas.
b) Ningún surfista es sacerdote, porque todos los sacerdotes son hombres y algunos surfistas no son hombres.
c) Algunas autoras son feministas, ya que algunas mujeres son autoras y otras feministas.
d) Todos los mosquitos son portadores potenciales de enfermedades; por lo tanto, algunos mosquitos son una amenaza para la sociedad, ya que todos los posibles portadores de enfermedades son una amenaza para la sociedad.
(e) Debido a que algunos neonazis son blogueros, algunos neonazis no son genios, ya que ningún genio es bloguero.

2. Pruebe la validez de las siguientes formas silogísticas.

a) EAE-2
b) EAE-3
c) OAO-3 d
) EIO-4 e
) AOO-4 f
) IAI-1 g
) AII-1

3. Pruebe los siguientes argumentos de validez.

a) Algunos piratas son mercenarios; de ahí que algunos marineros sean piratas, porque todos los marineros son mercenarios.
b) Algunas mujeres no son monjas, pero todas las monjas son novios; de ello se deduce que algunas mujeres no son novios.
c) Algunos republicanos no son políticos, porque algunos republicanos no son cristianos, y algunos cristianos no son políticos.

4. Probar la validez de los argumentos en el Ejercicio 1.