3.5: Problemas con la Plaza de la Oposición

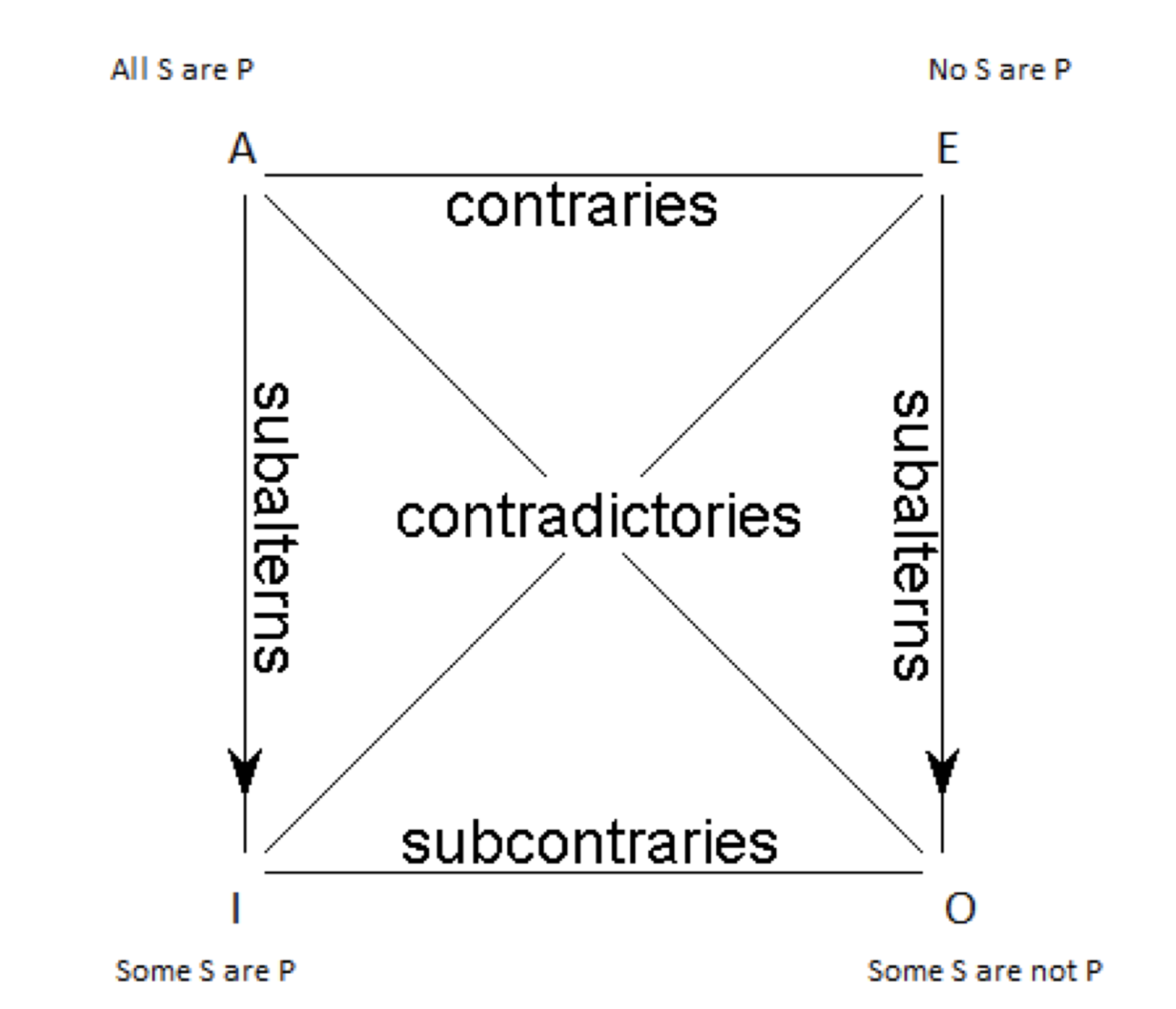
El Cuadrado de la Oposición es una herramienta sumamente útil: resume cuidadosamente, en forma gráfica, todo lo que sabemos sobre las relaciones entre los cuatro tipos de una proposición categórica.

Excepto, en realidad, no sabemos esas cosas. Lo siento, pero cuando presenté por primera vez la Plaza de la Oposición e hice el caso de las diversas relaciones que representa, te estaba guiando por el proverbial camino de la primavera. Lo que parecía fácil de hecho no es tan sencillo como parece. Algunas de las relaciones en la Plaza se rompen bajo ciertas circunstancias y nos obligan a hacer un poco de reflexión sobre cómo proceder. Es hora de explorar el “camino empinado y espinoso” que se abre ante nosotros cuando profundizamos un poco en los problemas que pueden surgir para la Plaza de la Oposición.

Importación Existencial

Para explicar cuáles son estos problemas, necesitamos el concepto de importación existencial (E.I. para abreviar). E.I. es una propiedad que las proposiciones pueden o no tener. Una proposición tiene importancia existencial cuando su verdad implica la existencia de algo. Por lo que decidimos significar cuando usamos la palabra 'algunos' —es decir, 'hay al menos uno' —las proposiciones particulares yo y O claramente tenemos E.I. Para que 'Algunos marineros no son pirates' para ser verdad, tiene que existir al menos un marinero que no sea pirata. De nuevo, eso es sólo una consecuencia de lo que queremos decir con 'algunos'.

Además, dadas las relaciones que se dice que sostiene la Plaza de la Oposición, las proposiciones universales A y E también tienen importancia existencial. Esto se debe a que las proposiciones particulares son subalternas. La verdad de una proposición universal implica la verdad de una particular: si una A es verdadera, entonces el yo correspondiente debe ser; si una E es verdadera, entonces la O correspondiente debe ser. Entonces, dado que la verdad de los universales implica la verdad de los particulares, y los particulares tienen E.I., entonces los universales implican también la existencia de algo: también tienen importancia existencial.

Problemas para la Plaza

Bien, las cuatro proposiciones categóricas tienen importancia existencial. ¿Cuál es el problema? Bueno, este hecho lleva a problemas. Consideremos la proposición de que todos los C.H.U.D.s son republicanos; también, considere la proposición de que algunos C.H.U.D.s no son republicanos. Ambas proposiciones son falsas. Eso es porque ambos implican la existencia de cosas —es decir, C.H.U.DS— que no existen. ('C.H.U.D.' significa 'Caníbalista Humanoide Underground Dweller'. Son los monstruos aterradores titulares de una tonta película de terror de los 80. No son reales.) 'Algunos C.H.U.D.s no son republicanos' afirma que existe al menos un C.H.U.D. que no es republicano; pero ese no es el caso, ya que no hay C.H.U.D.s. 'Todos los C.H.U.D.s son republicanos' también es falso: si fuera cierto, su subalterno 'Algunos C.H.U.D.s son republicanos' tendría que ser cierto; pero no puede ser, porque afirma que existe tal cosa como un C.H.U.D. (que es republicano).

En pocas palabras: Las proposiciones A y O sobre C.H.U.D.s ambas resultan falsas. Esto es un problema para la Plaza de la Oposición porque A y O se supone que son una pareja contradictoria; se supone que tienen valores de verdad opuestos.

Se pone peor. Cada vez que tu clase de materia está vacía —es decir, como 'C.H.U.D.s', no tiene ningún miembro— las cuatro proposiciones categóricas resultan falsas. Esto se debe a que, como vimos, los cuatro tienen importancia existencial. Pero si E y yo somos falsos, eso es un problema: se supone que son contradictorios. Si yo y O somos ambos falsos, eso es un problema: se supone que son subcontrarios. Cuando hablamos de clases de materias vacías, las relaciones representadas en la Plaza dejan de mantenerse.

¿Solución?

Entonces los problemas son causados por clases vacías. Podemos arreglarlo. Estamos construyendo nuestra propia lógica desde cero aquí arriba. El primer paso en ese proceso es domar el lenguaje natural. El hecho de que el lenguaje natural contenga términos que no se refieren a nada real parece ser una de las formas en que es rebelde, en necesidad de ser domesticado. ¿Por qué no limitarnos simplemente a términos de clase que realmente se refieren a las cosas, descartan clases vacías? Entonces se guarda la Plaza.

Si bien es tentadora, esta solución va demasiado lejos. El hecho es que hacemos afirmaciones categóricas usando términos de clase vacíos (o al menos posiblemente vacíos) todo el tiempo. Si los descartamos, se perdería nuestra capacidad de evaluar argumentos que contengan tales afirmaciones, y nuestra lógica quedaría empobrecida.

Un campo en el que la lógica es indispensable es la matemática. Los matemáticos necesitan un lenguaje preciso para demostrar afirmaciones interesantes. Pero algunas de las afirmaciones más interesantes en matemáticas involucran clases vacías. Por ejemplo, en la teoría de los números, se puede probar que no hay un número primo más grande, continúan para siempre. En otras palabras, el término 'número primo mayor' se refiere a una clase vacía. Si nuestra lógica descartaba términos de clase vacíos, los matemáticos no podrían usarlo. ¡Pero los matemáticos son algunos de nuestros mejores clientes!

También, los físicos. Antes de que se confirmara su existencia en 2013, hicieron diversas afirmaciones sobre una partícula fundamental llamada bosón de Higgs. “Los bosones de Higgs tienen cero giro”, podrían decir, haciendo una afirmación afirmativa universal sobre estas partículas. Pero antes de 2013, ni siquiera sabían si existían tales partículas. SI existieran, tendrían giro cero (y cierta masa, etc.); las ecuaciones predijeron tanto. Pero esas ecuaciones se basaron en suposiciones que quizás no hayan sido ciertas, por lo que puede que no haya habido ninguna partícula de este tipo. Sin embargo, era completamente apropiado hacer afirmaciones al respecto, a pesar de que 'bosón de Higgs' podría ser un término vacío.

Hacemos afirmaciones universales en la vida cotidiana que no nos comprometen con la existencia de las cosas. Considera la posible amonestación de un líder militar particularmente duro: Los desertores serán fusilados. Se trata de una afirmación afirmativa universal. Pero no se compromete con la existencia de desertores; de hecho, ¡su propósito mismo es asegurar que la clase permanezca vacía!

Entonces, las clases vacías tienen sus usos, y no queremos comprometernos con la existencia de las cosas cada vez que afirmamos un reclamo universal. Descartar clases vacías de nuestra lógica va demasiado lejos para salvar la Plaza de la Oposición. Necesitamos una solución alternativa a nuestros problemas.

Solución booleana

Abogada por el lógico inglés George Boole en el siglo XIX, nuestra solución a los problemas planteados será abandonar el supuesto de que las proposiciones universales (A y E) tienen importancia existencial, permiten clases vacías y aceptar las consecuencias. Esas consecuencias, ay, son bastante nefastas para la tradicional Plaza de la Oposición. Muchas de las relaciones que representa no se mantienen cuando las clases de materias están vacías.

Primero, las proposiciones particulares (I y O) ya no son subcontrarias. Desde que empiezan con la palabra 'algunos', tienen importación existencial. Cuando sus clases de materias están vacías, como ahora está permitido, ambas resultan falsas. Los subcontrarios no pueden ser ambos falsos, pero yo y O pueden ser ambos falsos cuando permitimos clases vacías.

A continuación, las proposiciones particulares ya no son subalternas de sus correspondientes universales (A y E). Como decíamos, los universales ya no tienen importancia existencial —ya no implican la existencia de nada— y así su verdad no puede implicar las verdades de proposiciones particulares, que siguen teniendo E.I.

Las únicas dos relaciones que quedan ahora en la Plaza son contradictoriedad —entre A y O, E e I— y la contrariedad entre los dos universales. Y estos están en conflicto cuando tenemos clases de materia vacías. En tales casos, tanto yo como O son falsos, como hemos dicho. De ello se deduce que sus contradictorias, A y E, deben ser ciertas. Pero, A y E se supone que son una pareja contraria; ambas no pueden ser ciertas. Así que no podemos mantener tanto la contrariedad como la contradictoriedad; hay que ir. Vamos a mantener la contradictoriedad. Hacer lo contrario sería abandonar los significados claros de las palabras que estamos usando. Hay una razón por la que introduje primero esta relación: es la más fácil de entender. Si quieres contradecir mi afirmación afirmativa universal de que todos los marineros son piratas, dices que algunos de ellos no lo son; A y O son claramente contradictorios. Al igual que E y yo: si quieres contradecir mi afirmación de que ningún surfista es sacerdote, muéstrame uno que es. Entonces eliminamos la contrariedad: es posible, en los casos en que la clase de sujeto está vacía, que ambas proposiciones A y E sean ciertas.

Lo que nos queda después de hacer estas revisiones ya no es un cuadrado, sino una X. Todo lo que queda es contradictoriedad:

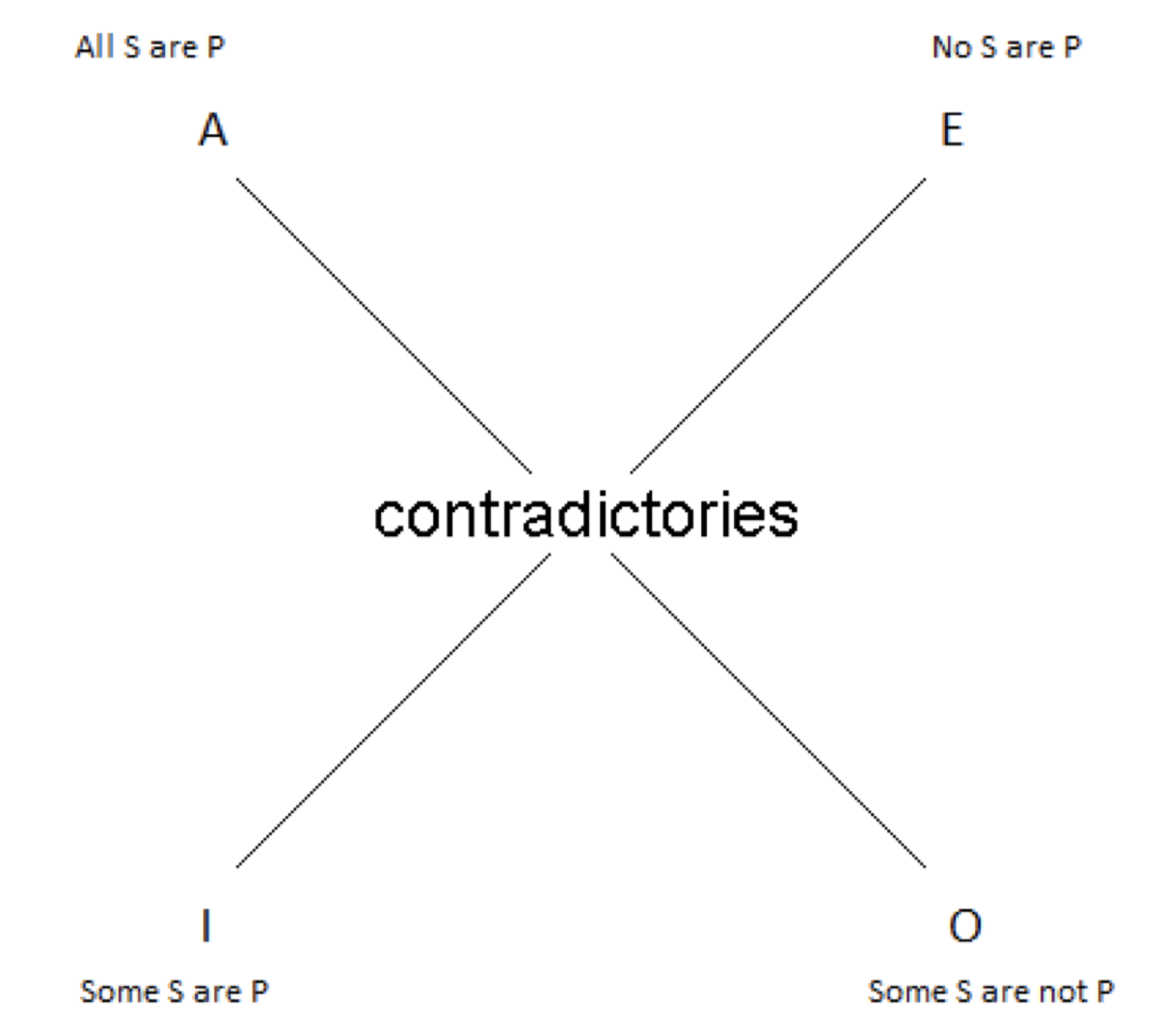
Y nuestra solución no está exenta de torpezas. En los casos en que la clase de sujeto está vacía, ambas proposiciones particulares (I y O) son falsas; sus contradictorias universales (E y A), entonces, son ciertas en esas circunstancias. Esto es extraño. Ambas frases expresan verdades: 'Todos los C.H.U.D.s son republicanos' y 'Ningún C.H.U.D.s son republicanos'. Esa es una pastilla dura de tragar, pero tragarla debemos, dadas las consideraciones anteriores. Podemos hacer que sea un poco más fácil de tragar si decimos que son ciertas, pero de manera vaga o trivial. Es decir, son verdad, pero no de una manera que te diga nada sobre cómo son realmente las cosas en el mundo (el mundo está, después de todo y por suerte, libre de C.H.U.D.).

Que terminaríamos eligiendo esta interpretación de los categóricos, más que aquella bajo la cual las proposiciones universales tenían importancia existencial, fue presagiado antes, cuando presentamos por primera vez los cuatro tipos de proposiciones categóricas y hablamos de cómo trazarlas. Elegimos diagramas para A y E que no implicaban la existencia de nada. Recordemos que nuestra manera de indicar la existencia en los diagramas de Venn es dibujar una X. Así que para una afirmación particular —algunos surfistas son sacerdotes, dicen— dibujamos esta imagen (siendo la X el único sacerdote surfista del que estamos comprometidos con la existencia de):

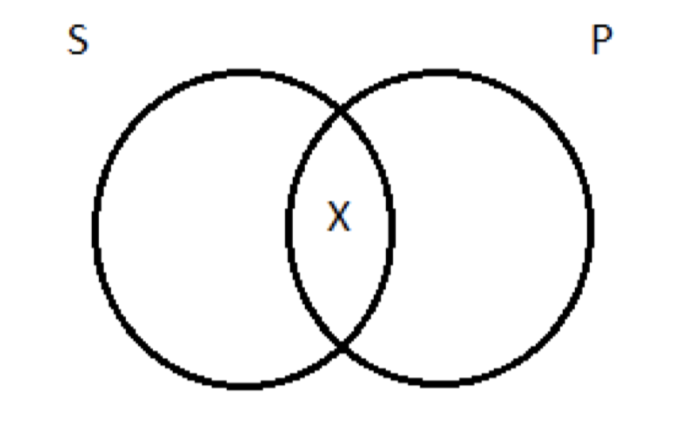
Los diagramas para los universales (A y E), sin embargo, no tenían X en ellos, solo sombreado; no nos comprometen a la existencia de nada. Si fuéramos a mantener la importación existencial de A y E, habríamos dibujado diferentes diagramas. Para lo afirmativo universal —todos los logísticos son imbéciles, digamos— ocultaríamos la porción del círculo de la izquierda que no se solapa con la derecha, para indicar que no existe tal cosa como un lógico que no sea un imbécil. Pero también pondríamos una X en la región media, para indicar que hay al menos un lógico que está (importación existencial):

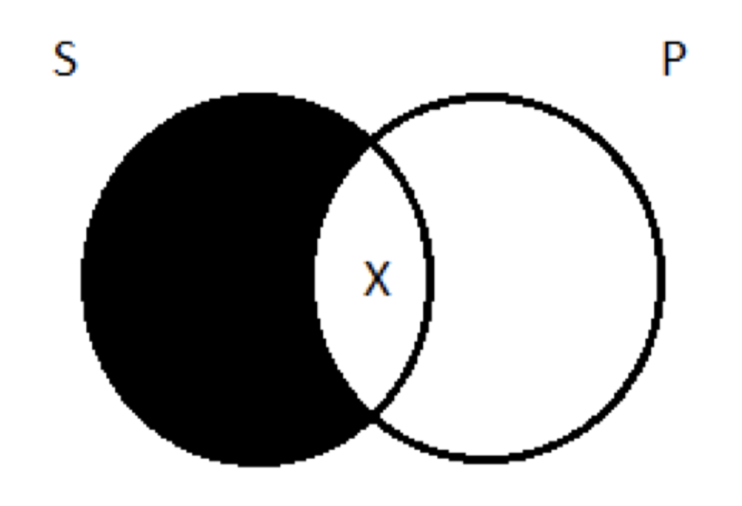
Y para lo negativo universal —ninguna mujer es sacerdote, digamos—, ocultaríamos la región media, para indicar que no hay nada que sea tanto mujer como sacerdote. Pero también pondríamos una X en el círculo de la izquierda, para indicar que hay al menos una mujer que no es sacerdote:

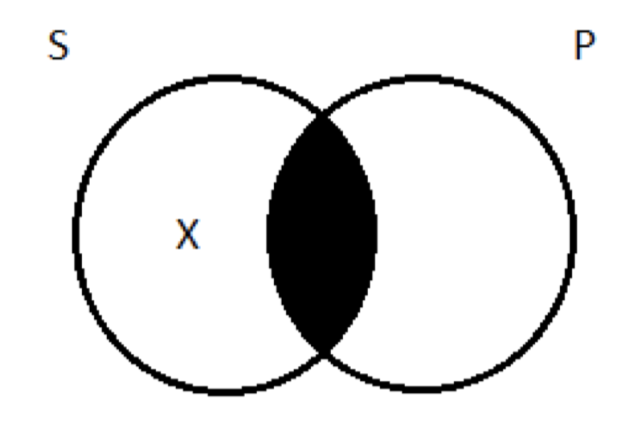
Esta interpretación de las proposiciones universales, según las cuales tienen importancia existencial, a menudo se llama la interpretación “aristotélica” (a diferencia de nuestra interpretación “booleana”, según la cual no). (No está claro, sin embargo, que sea correcto atribuir esta visión a Aristóteles. Si bien claramente sí creía que las proposiciones afirmativas universales (A) tenían importancia existencial, no está claro que pensara lo mismo de los negativos universales. Su interpretación del negativo particular (O) fue 'No todas las S son P', lo que podría ser (trivialmente, vacuamente) cierto cuando S está vacío. En ese caso, siendo O el subalterno de E no nos obliga a atribuir Importación Existencial a esta última. Para discusión, véase Parsons, Terence, “The Traditional Square of Opposition”, The Stanford Encyclopedia of Philosophy (Summer 2015 Edition), Edward N. Zalta (ed.), URL = < http://plato.stanford.edu/archives/s...ntries/square/ >) Qué interpretación se adopta marca la diferencia. Hay algunos argumentos que las dos interpretaciones evalúan de manera diferente: desde el punto de vista aristotélico, son válidos, pero en el punto de vista booleano, no lo son. Nos apegaremos a la interpretación booleana de los universales, según la cual no tienen importancia existencial.