4.5: Probando la Validez de la Lógica Sentencial

Habiendo tratado la tarea de domar el lenguaje natural, finalmente estamos en condiciones de completar el segundo y tercer paso de construir una lógica: definir la forma lógica y desarrollar una prueba de validez. La prueba implicará aplicar habilidades que ya aprendimos: establecer tablas de verdad y calcular los valores de verdad de los compuestos. Primero, debemos definir la forma lógica en SL.

Forma lógica en SL

Esto parecerá trivial, pero es necesario. Estamos aprendiendo a evaluar argumentos expresados en SL. Como cualquier evaluación de argumentos deductivos, el resultado depende de la forma del argumento. Entonces, ¿cuál es la forma de un argumento SL? Consideremos un ejemplo; aquí hay un argumento en SL:

A B
~B
Por lo tanto, ~ A

'A' y 'B' representan oraciones simples en inglés; no nos importa cuáles. Estamos trabajando dentro de SL: dado un argumento en este lenguaje, ¿cómo determinamos su forma? Simplemente, reemplazando sistemáticamente mayúsculas por variables (letras minúsculas como 'p', 'q' y 'r'). La forma de ese argumento particular de SL es la siguiente:

p q
~q
Por lo tanto, ~ p

La sustitución de mayúsculas por variables minúsculas fue sistemática en este sentido: cada ocurrencia de la misma letra mayúscula (e.g., 'A') fue reemplazada por la misma variable (e.g., 'p').

Para generar la forma lógica de un argumento SL, lo que hacemos es sustituir sistemáticamente las oraciones SL con lo que llamaremos formas de oración. Una oración SL es solo una combinación bien formada de símbolos SL: letras mayúsculas, operadores y paréntesis. Una forma de oración es una combinación de símbolos que estarían bien formados en SL, excepto que tiene variables minúsculas en lugar de letras mayúsculas.

Nuevamente, esto puede parecer un cambio trivial, pero es necesario. Recuerda, cuando estamos probando un argumento de validez, estamos comprobando si su forma es tal que es posible que sus premisas resulten verdaderas y su conclusión falsa. Esto significa verificar varias formas de rellenar el formulario con frases particulares. Las variables —como sugiere el nombre— pueden variar en la forma que necesitamos: son genéricas y pueden ser reemplazadas por cualquier oración particular antigua. Las construcciones reales de SL presentan letras mayúsculas, que son oraciones reales que tienen valores de verdad específicos. Es conceptualmente incoherente hablar de verificar diferentes posibilidades para oraciones reales. Por lo que debemos cambiar a los formularios de sentencia.

Prueba de validez de la tabla de la verdad

Para probar la validez de un argumento SL, identificamos su forma lógica, luego creamos una tabla de verdad con columnas para cada una de las variables y formas de oración en la forma del argumento. Rellenar columnas de Ts y Fs debajo de cada uno de los operadores en esos formularios de oración nos permitirá verificar lo que estamos buscando: una instancia de la forma del argumento para la cual las premisas resultan verdaderas y la conclusión resulta falsa. Encontrar tal instancia demuestra la invalidez del argumento, mientras que no encontrarla demuestra su validez.

Para ver cómo funciona esto, será útil trabajar a través de un ejemplo. Considere el siguiente argumento en inglés:

Si los demócratas recuperan el Congreso, se aprobarán muchas leyes nuevas.
Los demócratas no van a recuperar el Congreso.
Por lo tanto, no se aprobarán muchas leyes nuevas.

Lo evaluaremos traduciéndolo primero a SL. Que 'D' significa 'Los demócratas recuperan el Congreso' y 'L' significa 'Se aprobarán muchas nuevas leyes'. Este es el argumento en SL:

D L
~D
Por lo tanto, ~ L

Primero, la forma lógica. Al reemplazar 'D' por 'p' y 'L' por 'q', obtenemos:

p q
~p
Por lo tanto, ~ q

Ahora configuramos una tabla de verdad, con columnas para cada una de las variables y columnas para cada una de las formas de oración. Para determinar cuántas filas necesita nuestra tabla, observamos el número de variables diferentes que ocurren en el argument-form (llame a ese número 'n'); la tabla necesitará 2 ⁿ filas. En este caso, tenemos dos variables —'p' y 'q'—y así necesitamos 2 ² = 4 filas. (Si hubiera tres variables, necesitaríamos 2 ³ = 8 filas; si hubiera cuatro, 2 ⁴ = 16; y así sucesivamente). Aquí está la tabla que necesitamos rellenar para este ejemplo:

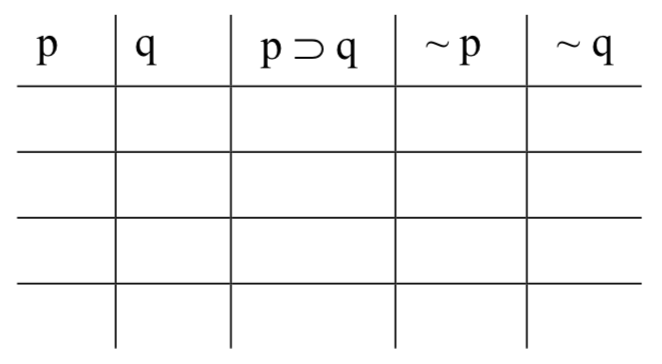
Primero, rellenamos las “columnas base”. Estas son las columnas para las variables. Esto lo hacemos sistemáticamente. Comience con la columna más a la derecha (debajo de 'q' en este caso), y complete Ts y Fs alternativamente: T, F, T, F, T, F,... tantas veces como necesite, hasta que tenga un valor de verdad en cada fila. Eso nos da esto:

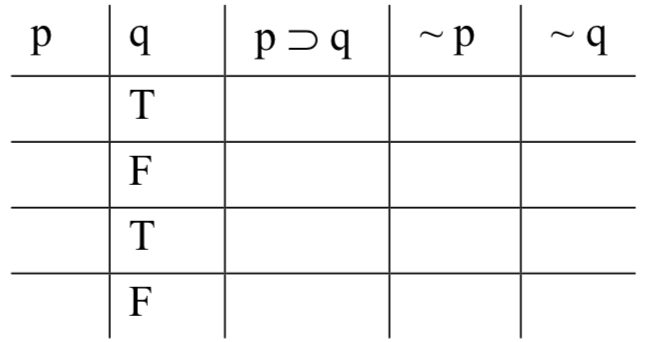
A continuación, nos movemos a la columna base a la izquierda de la que acabamos de rellenar (debajo de 'p' ahora), y rellenar Ts y Fs alternando en dos: T, T, F, F, T, T, F, F,... tantas veces como necesitemos. El resultado es este:

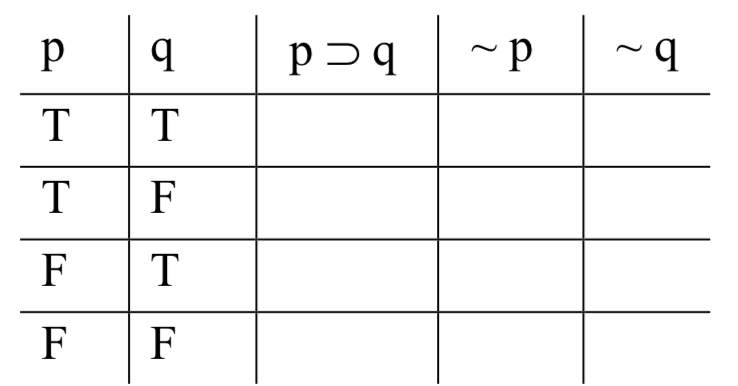
Si hubiera una tercera columna base, rellenaríamos los Ts y Fs alternando en cuatro patas: T, T, T, T, F, F, F, F, F, F... Para una cuarta columna base, alternaríamos entre ocho y otros. Y así sucesivamente.

A continuación, necesitamos rellenar columnas de Ts y Fs debajo de cada uno de los operadores en las columnas de los formularios-declaraciones. Para ello, aplicamos nuestro conocimiento de cómo calcular los valores de verdad de los compuestos en términos de los valores de sus componentes, consultando las definiciones de tablas de verdad de los operadores. Sabemos calcular los valores de p q: es falso cuando p es verdadero y q falso; true de lo contrario. Sabemos calcular los valores de ~ p y ~ q: esos son solo los opuestos de los valores de p y q en cada una de las filas. Haciendo estos cálculos, llenamos la tabla así:

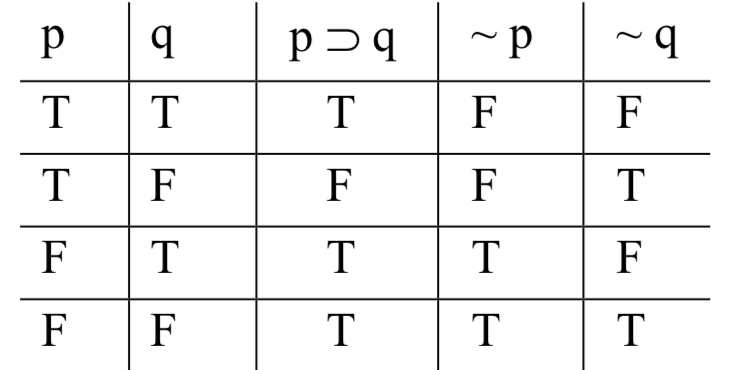
Una vez rellenada la tabla, comprobamos para ver si tenemos un formulario válido o no válido. La marca de una forma inválida es que es posible que las premisas sean verdaderas y la conclusión falsa. Aquí, las filas de la tabla son las posibilidades—los cuatro posibles resultados de conectar en particular oraciones SL para las variables: ambas verdaderas; la primera es verdadera, pero la segunda falsa; la primera falsa pero la segunda verdadera; ambas falsas. La razón por la que rellenamos sistemáticamente las columnas base como se describió anteriormente es que el método asegura que nuestras filas agotarán colectivamente todas estas combinaciones posibles.

Entonces, para ver si es posible que las premisas salgan verdaderas y la conclusión salga falsa, comprobamos cada una de las filas, buscando una en la que esto suceda, una en la que haya una T bajo 'p q', una T debajo de '~ p', y una F debajo de '~ q'. Y tenemos uno: en la fila 3, las premisas salen verdaderas y la conclusión sale falsa. Esto es suficiente para demostrar que el argumento no es válido:

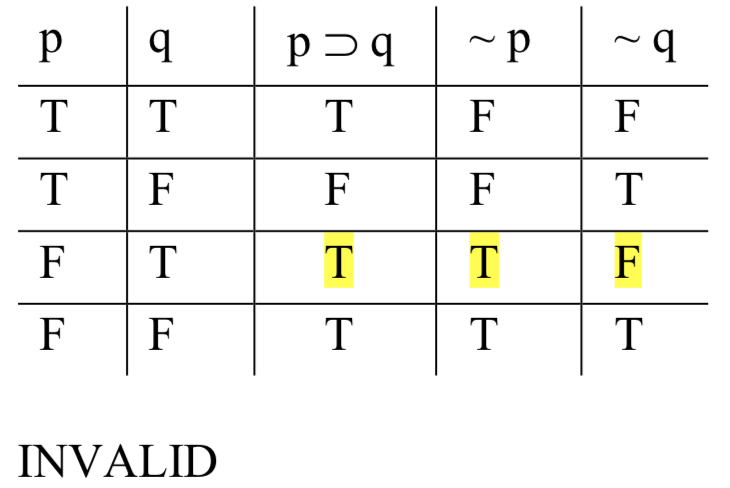
Cuando estamos comprobando la validez, estamos buscando una cosa, y una sola cosa: una fila (o filas) en la que las premisas salgan verdaderas y la conclusión salga falsa. Si encontramos uno, hemos demostrado que el argumento no es válido. Si no encontramos uno, eso indica que es imposible que las premisas sean verdaderas y que la conclusión sea falsa y así el argumento es válido. De cualquier manera, lo único que buscamos es una fila con verdaderas premisas y una conclusión falsa. Cada otro tipo de fila es irrelevante. Es común que los principiantes piensen erróneamente que lo son. La cuarta fila de la tabla anterior, por ejemplo, parece significativa. Todo sale cierto en esa fila. ¿Eso no significa algo, algo bueno, así el argumento es válido? No. Recuerde, cada fila representa una posibilidad; lo que muestra la fila 4 es que es posible que las premisas sean verdaderas y la conclusión verdadera. Pero eso no es suficiente para la validez. Para que un argumento sea válido, las premisas deben garantizar la conclusión; siempre que sean ciertas, la conclusión debe ser cierta. Que sea meramente posible que todos salgan verdad no es suficiente.

Veamos un ejemplo más involucrado, para ver cómo el cálculo de los valores de verdad de los formularios-declaraciones a veces debe proceder por etapas. La habilidad requerida aquí no es nada nuevo, es solo identificar a los operadores principales y calcular primero los valores de los componentes más simples, pero requiere mucha atención para mantener todo recto. Considera este argumento SL (no importa cuál es su contraparte inglesa):

(~ A • B) ‖ ~ X
B A Por
lo tanto, ~ X

Para obtener su forma, reemplazamos 'A' por 'p', 'B' por 'q', y 'X' por 'r':

(~ p • q) ‖ ~ r
q p Por
lo tanto, ~ r

Entonces nuestra tabla de verdad se verá así (ocho filas porque tenemos tres variables; 2 ³ = 8):

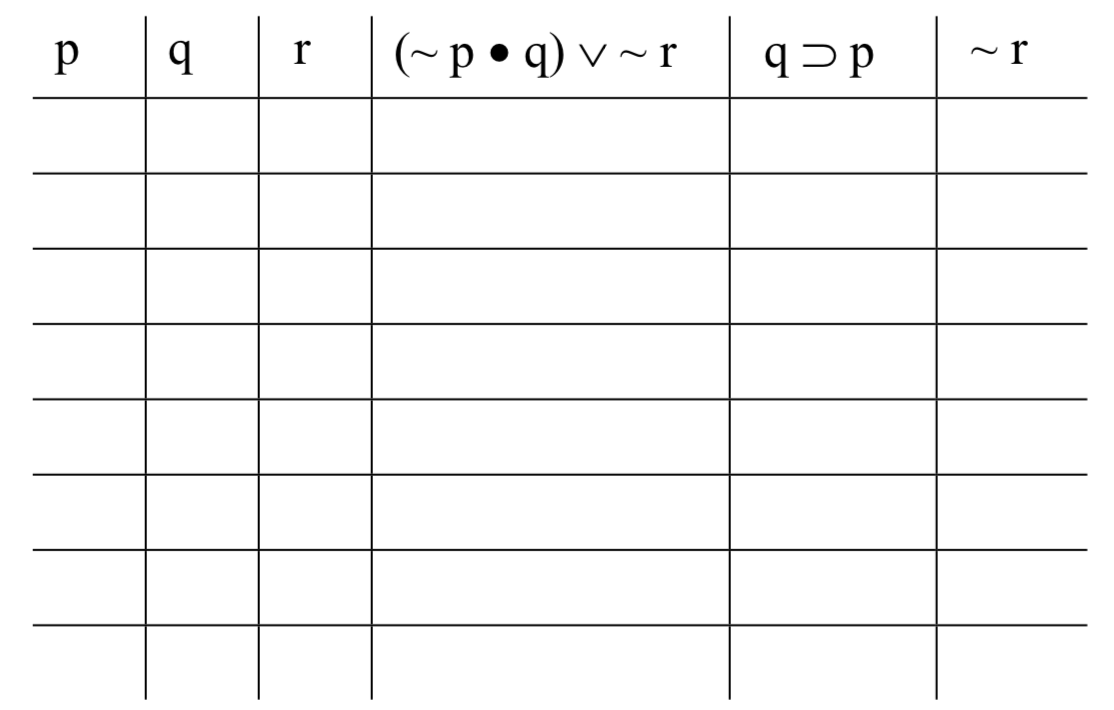
Rellenando las columnas base como se ha prescrito anteriormente, alternando entre sí para la columna debajo de 'r', cada dos bajo 'q', y cada cuatro bajo 'p', obtenemos:

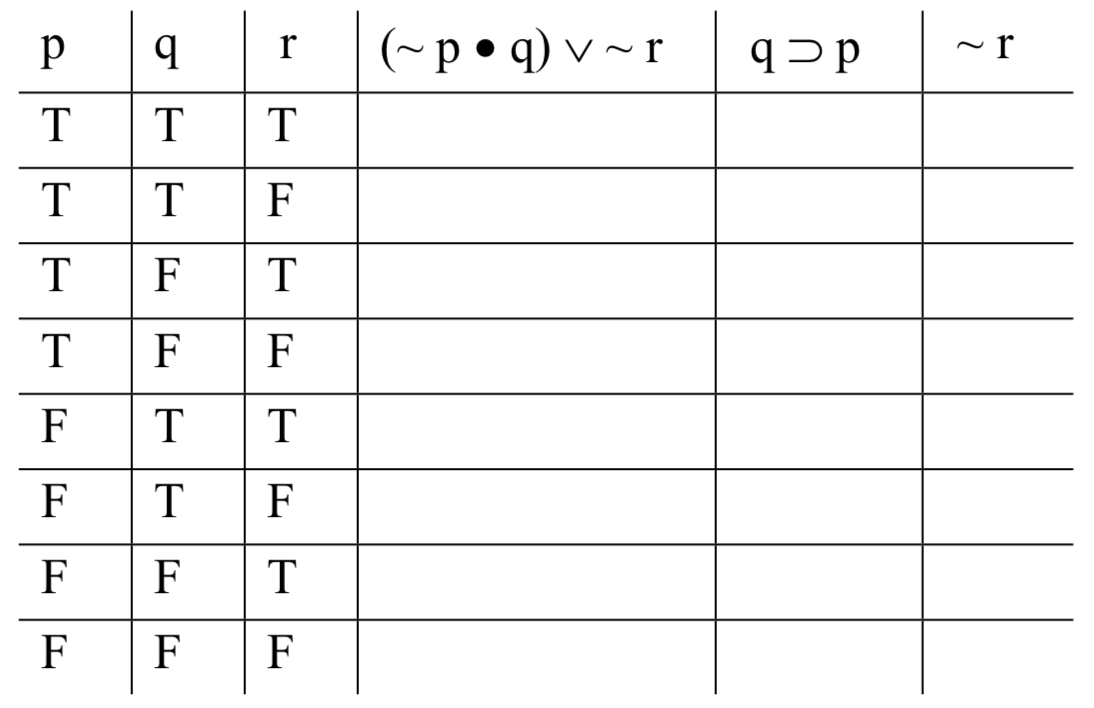
Ahora dirigimos nuestra atención a las tres formas de oración. Comenzaremos con la primera premisa, el compuesto '(~ p • q) ‖ ~ r'. Necesitamos calcular el valor de la verdad de esta fórmula. Sabemos cómo hacer esto, siempre que tengamos los valores de verdad de las partes más simples; ya hemos resuelto problemas como ese. La única diferencia en el caso de las tablas de verdad es que hay múltiples asignaciones diferentes de valores de verdad a las partes más simples. En este caso, hay ocho formas diferentes de asignar valores de verdad a 'p', 'q' y 'r'; esos son representados por las ocho filas diferentes de la tabla. Entonces estamos resolviendo un problema que sabemos resolver; solo lo estamos haciendo ocho veces.

Comenzamos por identificar al operador principal de la fórmula compuesta. En este caso, es la cuña: tenemos una disyunción; el disjunto de la izquierda es '(~ p • q)', y el disjunto de la derecha es '~ r'. Para averiguar qué sucede bajo la cuña en nuestra tabla, primero debemos averiguar los valores de estos componentes. Ambos disjuntos son ellos mismos compuestos: '(~ p • q)' es una conjunción, y '~ r' es una negación. Abordemos primero la conjunción. Para averiguar qué sucede bajo el punto, necesitamos conocer los valores de '~ p' y 'q'. Conocemos los valores de 'q'; esa es una de las columnas base. Debemos calcular el valor de '~ p'. Eso es fácil: en cada fila, el valor de '~ p' será justo lo opuesto al valor de 'p'. Observamos los valores bajo la tilde, el operador que los genera:

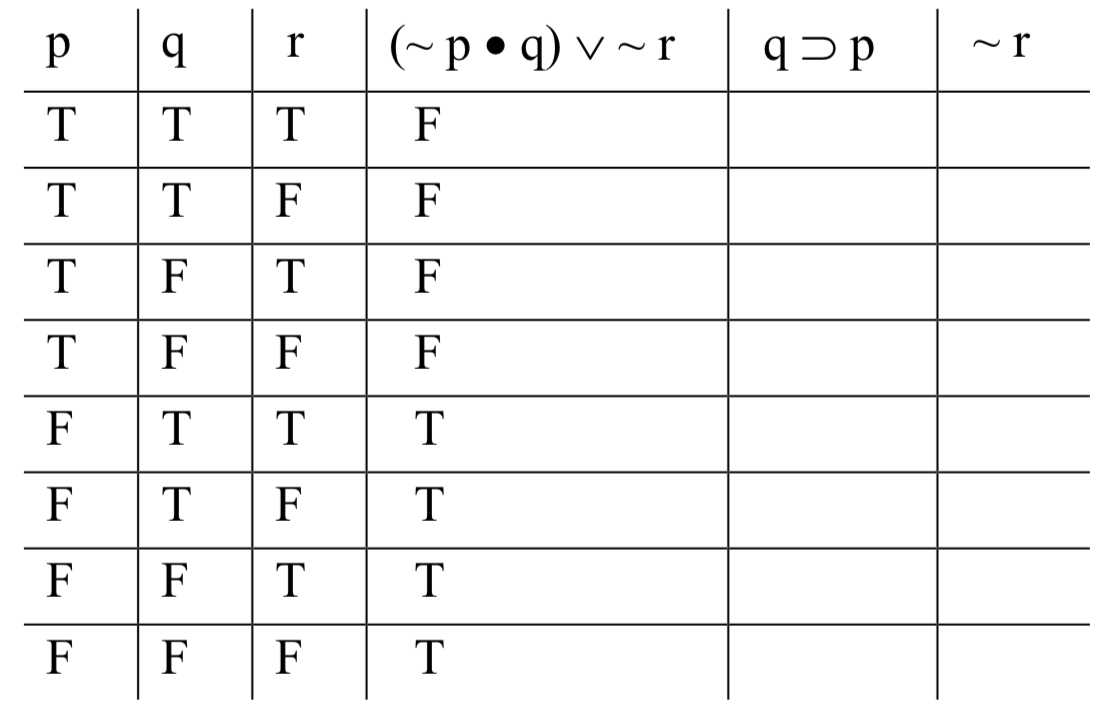
Para calcular el valor de la conjunción, consideramos el resultado, en cada fila, de la verdad-función para punto, donde las entradas son el valor bajo la tilde en '~ p' y el valor debajo de 'q' en la columna base. En las filas 1 y 2, es F • T; en las filas 3 y 4, F • F; y así sucesivamente. Los resultados:

La columna que acabamos de producir, debajo del punto, nos da el rango de valores de verdad para el disjunto de la izquierda en la primera premisa. Necesitamos los valores del disjunto de la derecha. Eso es solo '~ r', que es fácil de calcular: es solo el valor opuesto de 'r' en cada fila:

Ahora podemos finalmente determinar los valores de la verdad para toda la disyunción. Calculamos el valor de la función de verdad de la cuña, donde las entradas son las columnas debajo del punto, por un lado, y la tilde de '~ r' por el otro. F; F; F;;;;;;;;;;;;;;;;;;

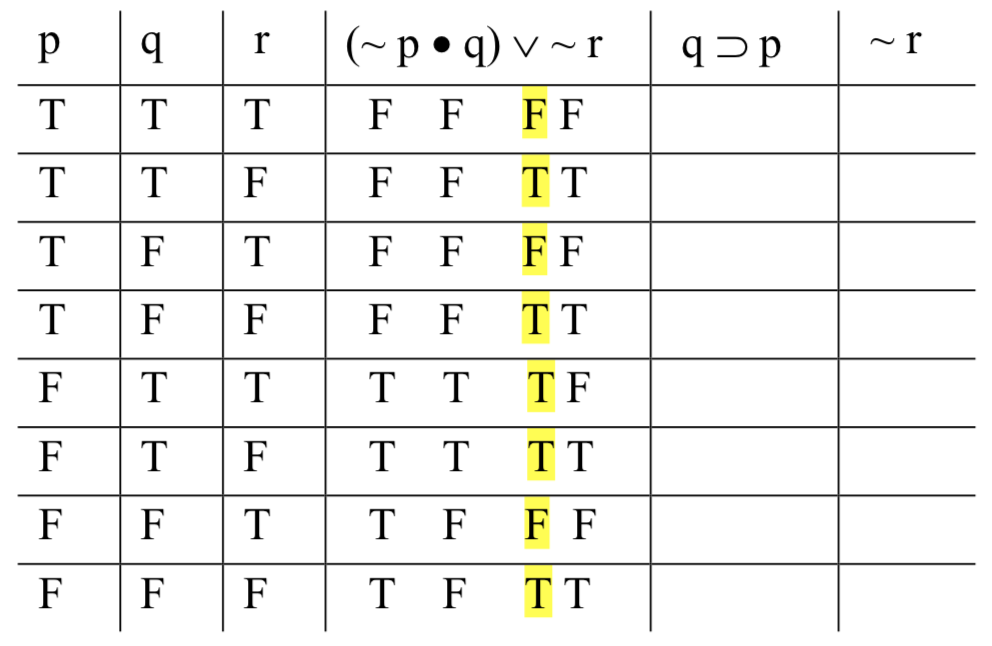
Dado que esa columna representa el rango de valores posibles para toda la forma de oración, la destacamos. Cuando probamos la validez, estamos buscando filas donde las premisas en su conjunto se hagan realidad; buscaremos el valor bajo sus principales operadores. Para hacerlo más fácil, solo para que no perdamos la noción de las cosas visualmente por todas esas columnas, destacamos la que está debajo del operador principal.

A continuación, la segunda premisa, que por suerte es mucho menos compleja. Es, sin embargo, un poco complicado. Tenemos que computar aquí el valor de un condicional. Pero fíjense que las cosas son un poco distintas de lo habitual: el antecedente, 'q', tiene su columna base a la derecha de la columna para el consecuente, 'p'. Eso es un poco incómodo. Estamos acostumbrados a computar condicionales de izquierda a derecha; tendremos que ajustarnos mentalmente al hecho de que 'q p' va de derecha a izquierda. (Alternativamente, si ayuda, simplemente puede reproducir las columnas base debajo de las variables en la columna 'q p'). Entonces en las dos primeras filas, calculamos T T; pero en las filas 3 y 4, es F T; en las filas 5 y 6, es T F (la única circunstancia en la que los condicionales resultan falsos); a en las filas 7 y 8, es F F. Aquí está el resultado:

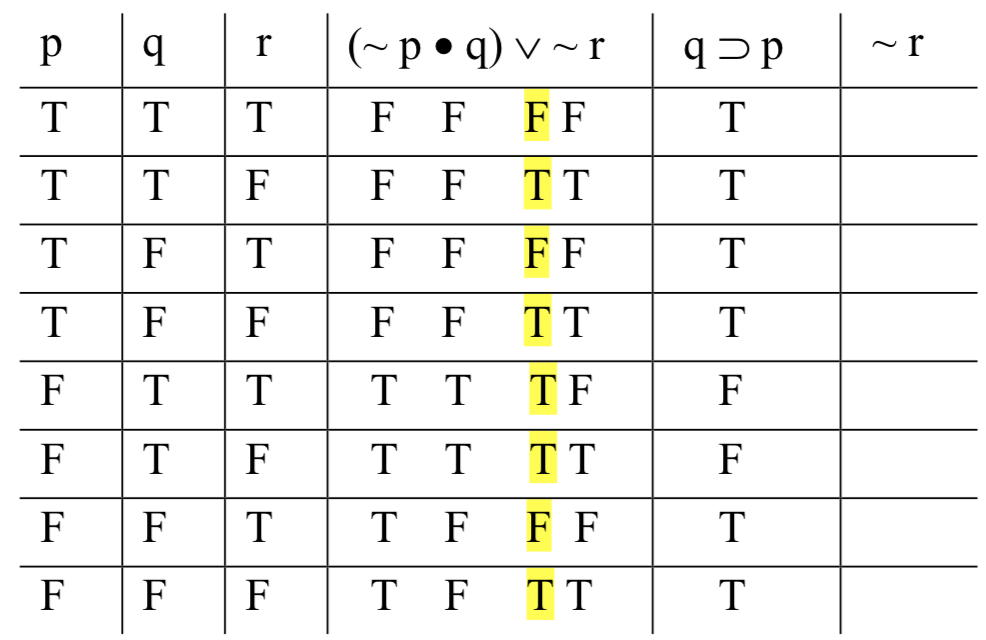
No hace falta resaltar esa columna, ya que es la única que producimos para esa premisa, por lo que no puede haber confusión.

Terminamos la tabla calculando los valores para la conclusión, lo cual es fácil:

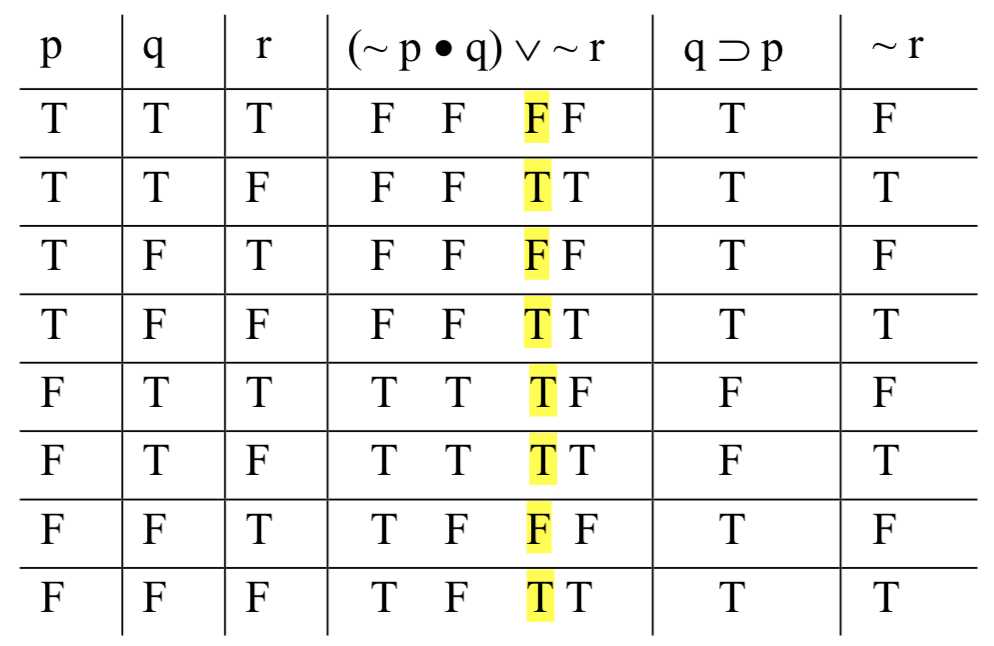
¿Es válido el argumento? Buscamos una fila con verdaderas premisas y una conclusión falsa. No hay ninguno. Las únicas dos filas en las que ambas premisas salen verdaderas son la segunda y la octava, y en ambas también tenemos una conclusión verdadera. Es imposible que las premisas sean verdaderas y la conclusión falsa, por lo que el argumento es válido.

Entonces así es como probamos argumentos de validez en SL. Es un procedimiento sencillo; la principal fuente de error es el simple descuido. Ve paso a paso, realiza un seguimiento cuidadoso de lo que estás haciendo, y debería ser fácil. Vale la pena señalar que la prueba de la tabla de verdad es lo que los lógicos llaman un “procedimiento de decisión”: es un proceso gobernado por reglas (un algoritmo) que está garantizado para responder a tu pregunta (en este caso: ¿válido o inválido?) en un número finito de pasos. Es posible programar una computadora para ejecutar la prueba de la tabla de verdad sobre argumentos SL arbitrariamente largos. Esto es reconfortante, ya que una vez que se obtienen más de cuatro variables más o menos, el proceso se vuelve difícil de manejar.

Ejercicios

Pruebe los siguientes argumentos de validez. Para aquellos que no sean válidos, especifique la (s) fila (s) que demuestre la invalidez.

1. ~ A, por lo tanto ~ A +' B

2. A B, ~ B, por lo tanto ~ A

3. A +' B, ~ A, por lo tanto ~ B

4. ~ (A ≡ B), A 6820 B, por lo tanto A • B

5. ~ (A B), ~ B ‖ ~ A, por lo tanto ~ (~ A ≡ B)

6. ~ B 6820 A, ~ A, A ≡ B, por lo tanto ~ B

7. A (B • C), ~ B +' ~ C, por lo tanto ~ A

8. ~ A 6820 C, ~ B ~ C, por lo tanto A ≡ C

9. ~ A ‖ (~ B • C), ~ (C ‖ B) A, por lo tanto ~ C ~ B

10. A +' B, B C, ~ C, por lo tanto ~ A