5.2: Compensación de serie

Una forma de cambiar el rendimiento de un sistema de retroalimentación es alterar la función de transferencia de su ruta de ganancia directa o su ruta de retroalimentación. Esta técnica de modificación de un elemento en serie en un sistema de bucle único se denomina compensación de serie. Los cambios pueden implicar la ganancia d-c de un elemento o su dinámica o ambas.

Ajuste de la ganancia D-C

Una modificación conceptualmente sencilla que se puede hacer a la transmisión de bucle es variar su valor d-c o de banda media\(a_0f_0\). Esta modificación tiene un efecto directo sobre la desensitividad de baja frecuencia, ya que hemos visto que la atenuación a los cambios en la ganancia de trayectoria directa proporcionada por la retroalimentación es igual a\(1 + a_0f_0\).

La dinámica de bucle cerrado también depende de la magnitud de la transmisión en bucle de baja frecuencia. El ejemplo que involucra la Figura 4.6 mostró cómo se utilizan los métodos de locus raíz para determinar la relación entre\(a_0f_0\) y la relación de amortiguación de un par de polos dominantes. Una segunda aproximación al control de la dinámica de bucle cerrado mediante el ajuste\(a_0f_0\) por un valor específico de\(M_p\) se utilizó en el ejemplo que involucra la Figura 4.24.

Una suposición común a ambos ejemplos anteriores fue que el valor de\(a_0f_0\) podría seleccionarse sin alterar las singularidades incluidas en la transmisión en bucle. Para ciertos tipos de sistemas de retroalimentación, la independencia de la magnitud d-c y la dinámica de la transmisión en bucle es realista. La dinámica de los servomecanismos, por ejemplo, generalmente está dominada por componentes mecánicos con anchos de banda menores a 100 Hz. Una porción de la transmisión de bucle d-c de un servomecanismo a menudo es proporcionada por un amplificador electrónico, y estos amplificadores pueden proporcionar ganancia independiente de la frecuencia en el rango de kilohercios o megahercios altos. Cambiar la ganancia del amplificador cambia el valor de\(a_0f_0\) pero deja la dinámica asociada con la transmisión en bucle prácticamente inalterada.

Este tipo de independencia está frecuentemente ausente en los amplificadores operacionales. Para aumentar la ganancia, es posible que haya que sumar etapas, produciendo cambios significativos en la dinámica. La disminución de la ganancia de una etapa de amplificación también puede cambiar la dinámica debido, por ejemplo, a una relación entre la capacitancia de entrada y la ganancia de voltaje de un amplificador de emisor común. Otra dificultad práctica surge porque generalmente no hay una manera predecible de cambiar la ganancia de bucle abierto d-c de los amplificadores operativos de circuito discreto o integrado disponibles a partir de los terminales disponibles.

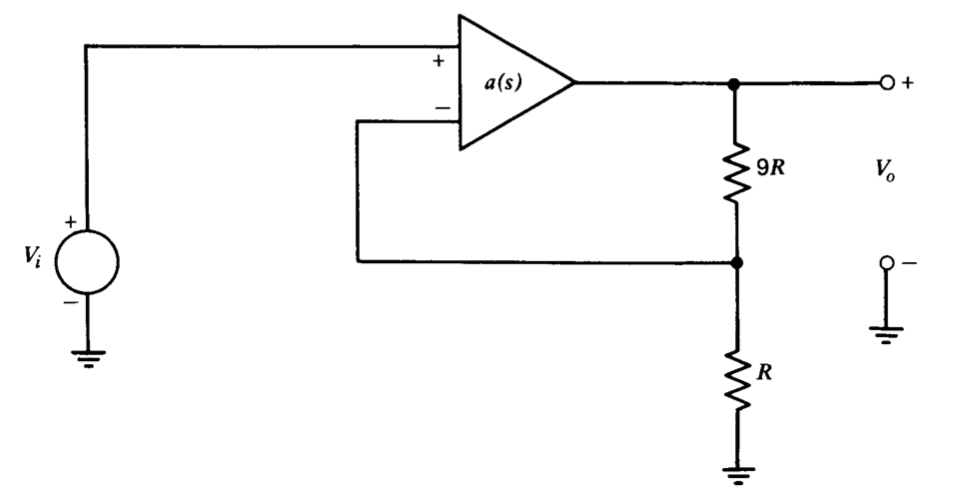
Un enfoque alternativo implica la modificación de la transmisión del bucle d-c por medio de la red de retroalimentación conectada alrededor del amplificador. La conexión de la Figura 5.1\(a\) ilustra una posibilidad. El diagrama de bloques para este amplificador, suponiendo una carga insignificante en la entrada o en la salida, se muestra en la parte b de esta figura, mientras que el diagrama de bloques después de la reducción a la forma de realimentación unitaria se muestra en parte\(c\). Si la resistencia\(R\) de derivación de la entrada inversora a tierra es un circuito abierto, el valor d-c de la transmisión en bucle está completamente determinado por\(a_0\) y la ganancia ideal de bucle cerrado\(-R_2/R_1\). Sin embargo, la inclusión de\(R\) proporciona un grado adicional de libertad para que la transmisión de bucle d-c y la ganancia ideal se puedan cambiar independientemente.

Esta técnica se ilustra para un inversor de ganancia unitaria (\(R_1 = R_2\)) y

\[a(s) = \dfrac{10^6}{(s +1)(10^{-5} s + 1)} \nonumber \]

Figura 5.1 Inversor. (\(a\)) Circuito. (\(b\)) Diagrama de bloques. (\(c\)) Diagrama de bloques reducido a forma de unidad-retroalimentación.

Figura 5.2 Gráfica de Bode de\(10^6/[(s + 1)(10^{-5} s + 1)]\).

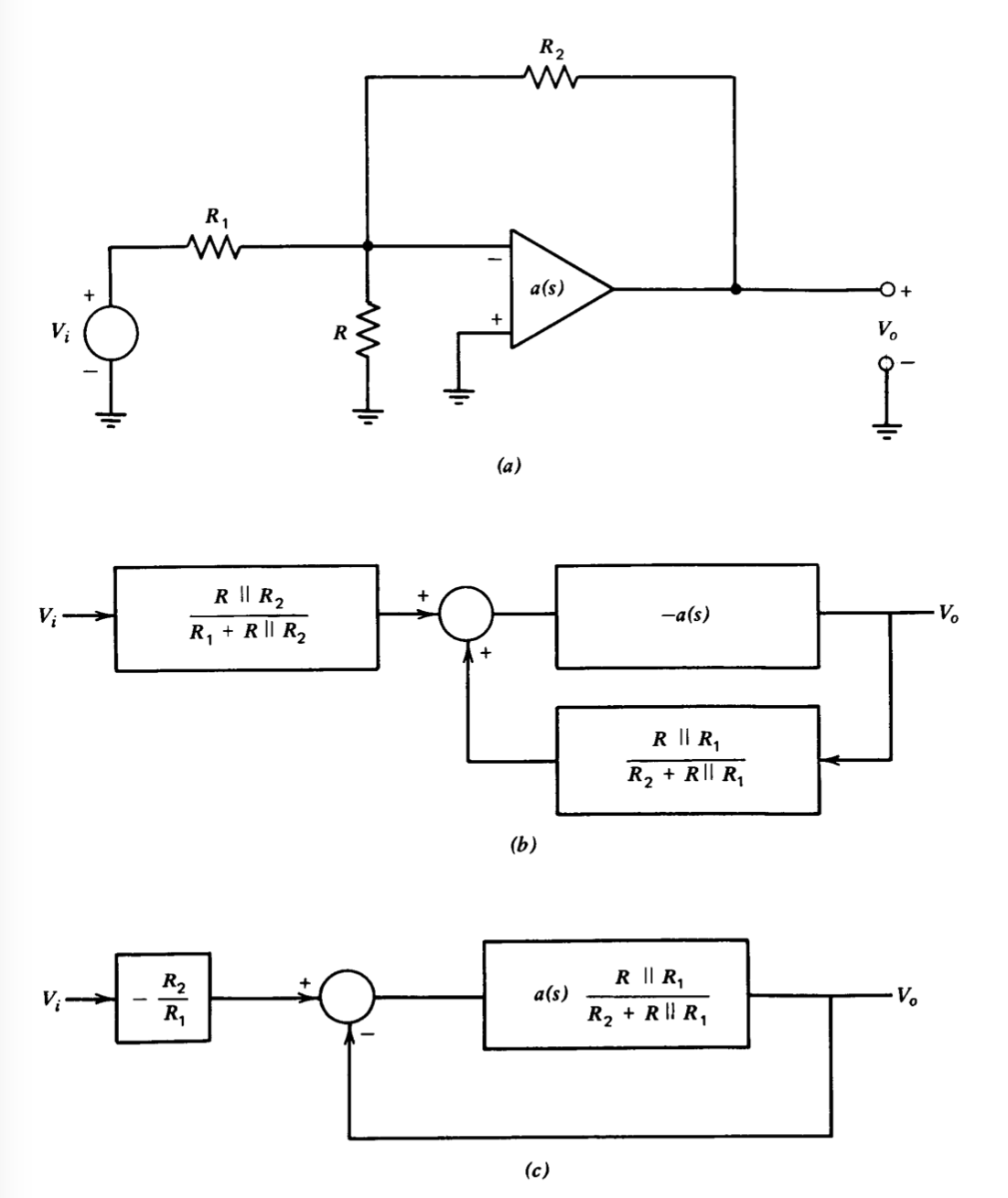
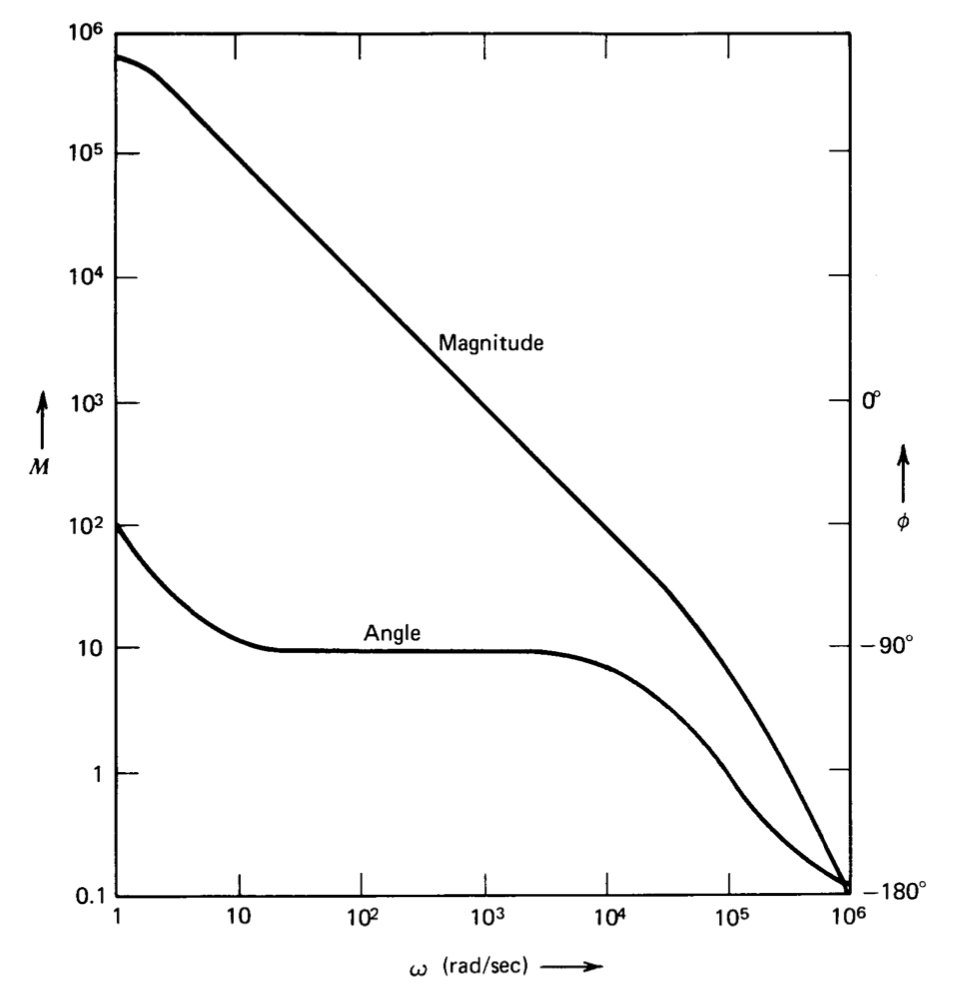
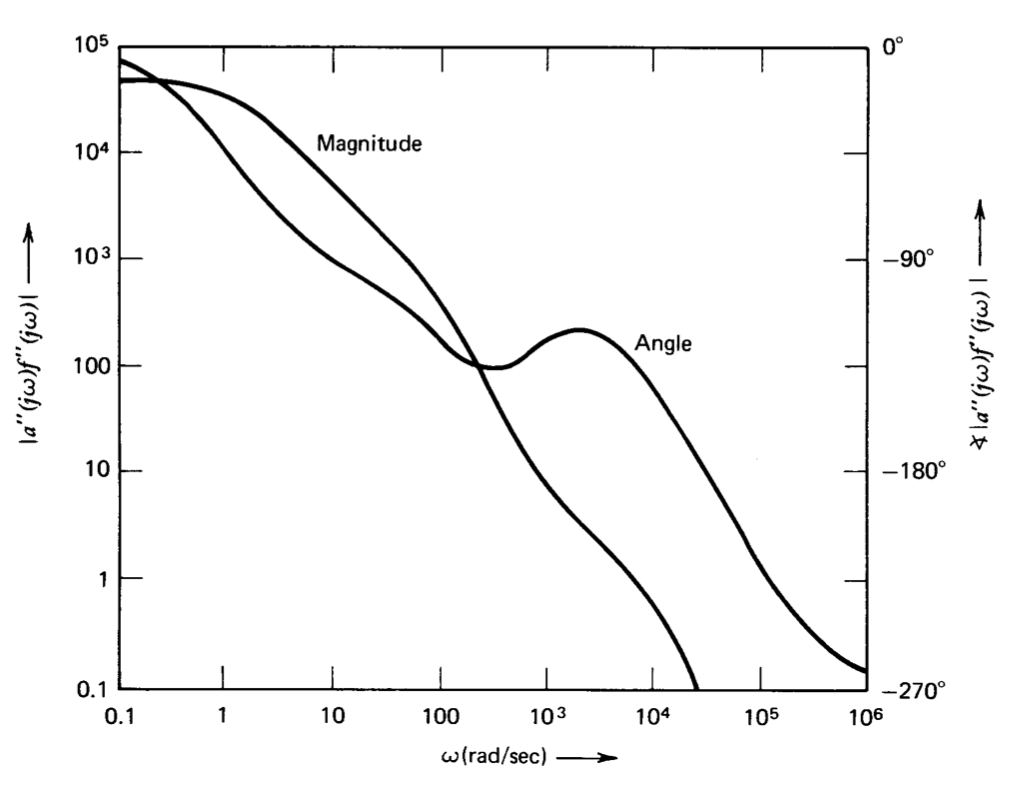
Una gráfica de Bode de esta función de transferencia se muestra en la Figura 5.2. Si\(R\) es un circuito abierto, la magnitud de la transmisión en bucle es de uno a aproximadamente\(2.15 \times 10^5\) radianes por segundo, ya que la magnitud de\(a(s)\) a esta frecuencia es igual al factor de dos atenuaciones proporcionadas por la\(R_1-R_2\) red. El margen de fase del sistema es\(25^{\circ}\), y la Figura 4.26\(a\) muestra que la relación de amortiguación de bucle cerrado es de 0.22. Dado que la Figura 4.26 se generó asumiendo este tipo de transmisión en bucle, arroja resultados exactos en este caso. Si la resistencia\(R\) se hace igual a\(0.2R_1\), la frecuencia de ganancia de unidad de transmisión de bucle se reduce a\(10^5\) radianes por segundo por la atenuación del factor de siete proporcionada por la red, y el margen de fase y la relación de amortiguación se incrementan a\(45^{\circ}\) y 0.42, respectivamente. Una penalización pagada por este tipo de atenuación en los terminales de entrada del amplificador es que el desplazamiento de voltaje y el ruido en la salida del amplificador se incrementan para un desplazamiento dado y el ruido en los terminales de entrada del amplificador (ver Problema P5.2).

Creando un Polo Dominante

Consideraciones elementales muestran que una transmisión de bucle unipolar da como resultado un sistema estable para cualquier cantidad de retroalimentación negativa, y que el ancho de banda de bucle cerrado de dicho sistema aumenta con el aumento\(a_0f_0\). De manera similar, si la transmisión de bucle en las proximidades de la frecuencia de ganancia unitaria está dominada por un polo, se obtiene fácilmente un amplio margen de fase. Debido a la facilidad de estabilizar sistemas aproximadamente unipolares, muchos tipos de compensación se reducen esencialmente para hacer que un polo domine la transmisión en bucle.

Un método de fuerza bruta para hacer que un polo domine la transmisión de bucle de un amplificador es simplemente conectar un condensador desde un nodo en la ruta de la señal a tierra. Si se usa un condensador lo suficientemente grande, la ganancia del amplificador caerá por debajo de uno a una frecuencia donde se puedan ignorar otros polos del amplificador. La desventaja obvia de este enfoque de compensación es que puede reducir drásticamente el ancho de banda de bucle cerrado del sistema.

Un sistema de retroalimentación diseñado para mantener constante el valor de su salida independientemente de las perturbaciones se denomina regulador.Dado que la salida no necesita rastrear una entrada que varía rápidamente, el ancho de banda de bucle cerrado es un parámetro sin importancia. Si se incluye un polo dominante en la porción de salida de un regulador, las características de paso bajo de este polo pueden mejorar realmente el rendimiento del sistema al atenuar las perturbaciones incluso en ausencia de retroalimentación.

Un posible tipo de regulador de voltaje se muestra de forma simplificada en la Figura 5.3. Se utiliza un amplificador operacional para comparar el voltaje de salida con una referencia fija. El amplificador operacional acciona una etapa reguladora en serie que consiste en un transistor con una resistencia emisora. El regulador en serie aísla la salida del circuito de una fuente de voltaje no regulada. La carga incluye una combinación de resistencia-condensador paralelo y una fuente de corriente perturbadora. La fuente de corriente se incluye para fines de análisis y se utilizará para determinar el grado en que el circuito rechaza los cambios de carga-corriente. Se supone que el polo dominante en el sistema se produce debido a la carga, y además se supone que el amplificador operacional y el transistor en serie no aportan dinámica a frecuencias donde la magnitud de la transmisión de bucle supera una.

El diagrama de bloques de la Figura 5.3\(b\) modela el regulador si se supone que la ganancia de corriente de base común del transistor es una y que la resistencia\(R\) es grande en comparación con el recíproco de la transconductancia del transistor. Este diagrama verifica la naturaleza unipolar de la transmisión en bucle del sistema.

Como se mencionó anteriormente, el objetivo de la circuitería es minimizar los cambios en la tensión de carga que resultan de cambios en la corriente perturbadora y la tensión no regulada. Las funciones de transferencia de bucle cerrado de perturbación a salida que indican qué tan bien el regulador logra este objetivo son

\[\dfrac{V_l}{I_d} = \dfrac{R/a_0}{RC_L s/a_0 + (1 + R/a_0 R_L)} \nonumber \]

y

\[\dfrac{V_l}{V_u} = \dfrac{1/a_0}{RC_L s/a_0 + (1 + R/a_0 R_L)} \nonumber \]

Figura 5.3 Regulador de voltaje. (\(a\)) Circuito. (\(b\)) Diagrama de bloques.

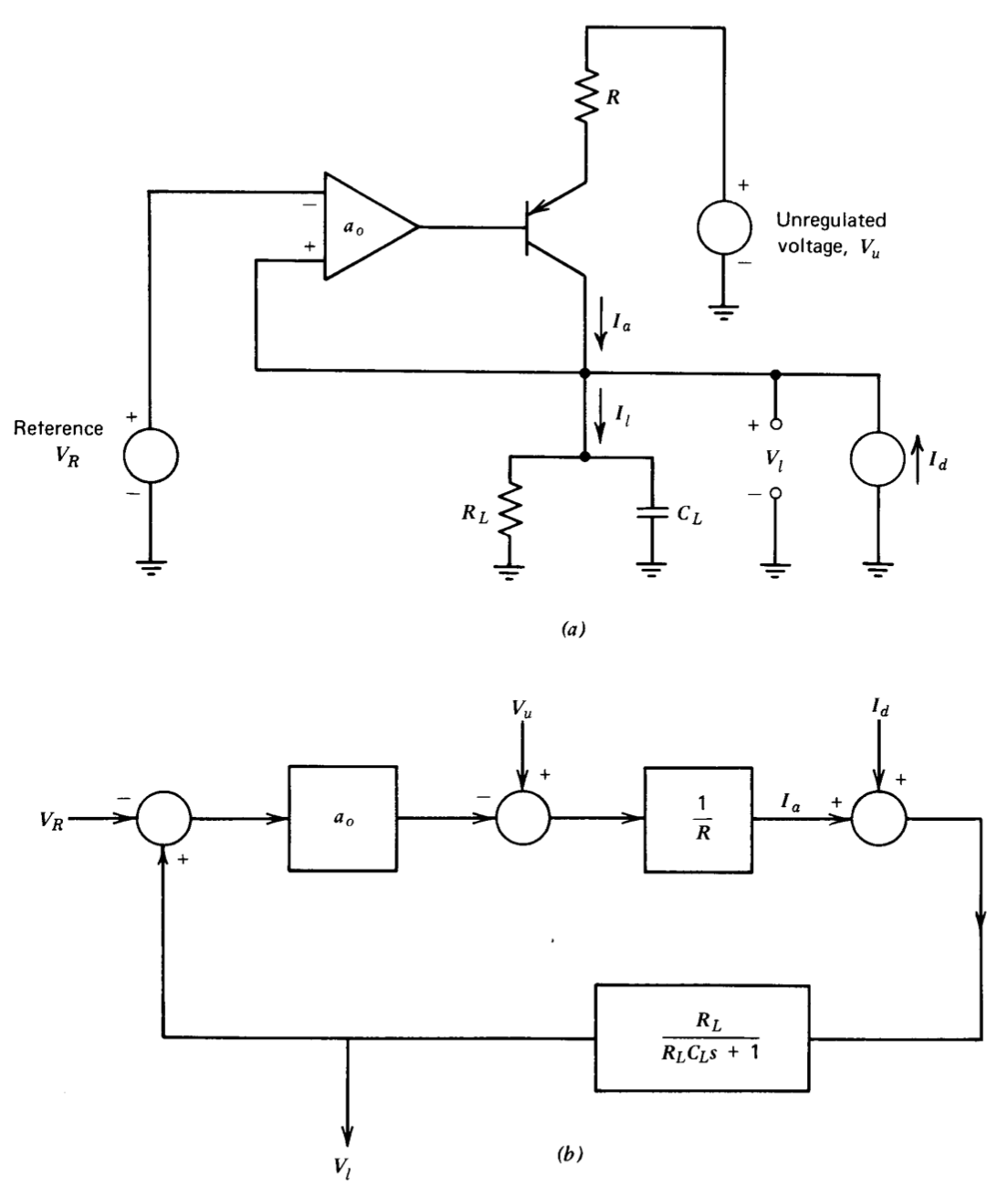
Si se consideran perturbaciones sinusoidales, la magnitud de cualquiera de las funciones de transferencia de perturbación a salida es un máximo en d-c, y disminuye al aumentar la frecuencia debido a las características de paso bajo de la carga. Incrementar\(C_L\) mejora el rendimiento, ya que disminuye la frecuencia a la que la perturbación se atenúa significativamente en comparación con su valor d-c. Si se asume que se pueden conectar cargas arbitrarias al regulador (que es la situación habitual, si, por ejemplo, este circuito se utiliza como fuente de alimentación de laboratorio), los valores de\(R_L\) y\(C_L\) deben considerarse variables. El valor mínimo de\(C_L\) puede restringirse al incluir un condensador con la circuitería de regulación. El valor del condensador de carga aumenta a medida que las cargas externas se conectan al regulador debido a los condensadores de desacoplamiento generalmente asociados con estas cargas. De igual manera,\(R_L\) disminuye con el aumento de la carga a algún valor mínimo determinado por las limitaciones de carga.

Figura 5.4 Efecto del cambio de parámetros de carga en la gráfica Bode de un regulador de voltaje.

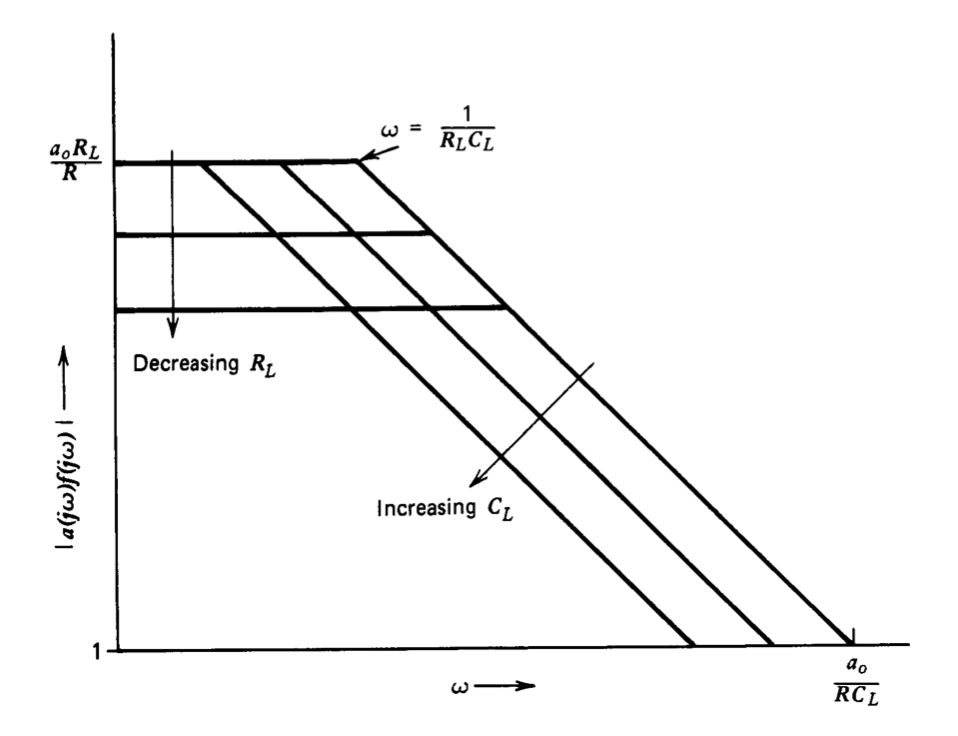
La compensación proporcionada por el polo a la salida del regulador mantiene la estabilidad a medida que\(R_L\) cambia CL, como se ilustra en la gráfica Bode de la Figura 5.4. (El negativo de la transmisión en bucle para esta gráfica es\(a_0R_L/ R(R_LC_Ls + 1)\), determinado directamente a partir de la Figura 5.3)\(b\). Tenga en cuenta que la frecuencia de ganancia unitaria se puede limitar limitando el valor máximo de la\(a_0/RC_L\) relación y, por lo tanto, el cruce se puede forzar antes de que otros elementos del sistema afecten la dinámica. El margen de fase del sistema permanece cerca de\(90^{\circ}\) como\(R_L\) y\(C_L\) varía en amplios límites.

Compensación de plomo y retraso

Si el diseñador es libre de modificar la dinámica de la transmisión en bucle así como su magnitud de baja frecuencia, tiene considerablemente más control sobre el rendimiento de bucle cerrado del sistema. Ya se ha discutido la modificación bastante simple de hacer que un solo polo domine.

Los tipos de cambios que se pueden hacer a la dinámica de la transmisión en bucle están restringidos, incluso en sistemas puramente matemáticos. Es tentador pensar que los sistemas podrían mejorarse, por ejemplo, agregando desplazamiento de fase positivo a la transmisión en bucle sin cambiar sus características de magnitud. Esta modificación mejoraría claramente el margen de fase de un sistema. Desafortunadamente, las características de magnitud y ángulo de las funciones de transferencia físicamente realizables no son independientes, y las funciones de transferencia que proporcionan desplazamiento de fase positivo también tienen una magnitud que aumenta al aumentar la frecuencia. El aumento de magnitud puede resultar en una frecuencia de cruce del sistema más alta, y el desplazamiento de fase negativo adicional que resulta de otros elementos en el bucle puede negar las ventajas esperadas.

La forma en que se implementa la compensación en serie y los tipos de funciones de transferencia compensadoras que se pueden obtener en sistemas prácticos están aún más limitados por las realidades de hardware del sistema de retroalimentación que se compensa. El diseñador de un servomecanismo normalmente cuenta con una amplia variedad de funciones de transferencia compensadora a su disposición, ya que las redes eléctricas y amplificadores utilizados habitualmente para compensar los anismos de servomech tienen un ancho de banda prácticamente ilimitado en relación con las partes mecánicas del sistema. Por el contrario, debemos recordar que las opciones del diseñador del amplificador de retroalimentación son más restringidas porque las formas en que se puede cambiar la función de transferencia de un amplificador, particularmente cerca de su frecuencia de ganancia unitaria donde las limitaciones de ancho de banda del transistor dominan el rendimiento, a menudo están severamente restringidas .

Figura 5.5 Red de plomo.

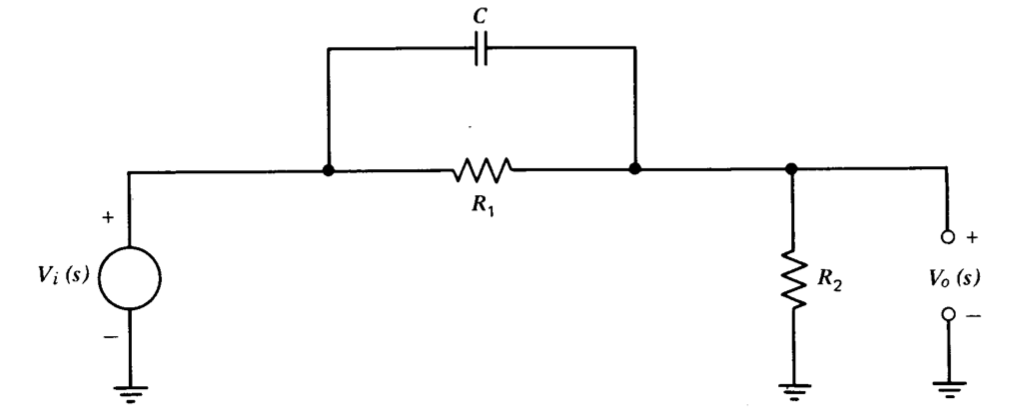
Normalmente se utilizan dos tipos distintos de funciones de transferencia para la compensación en serie de sistemas de retroalimentación, y estos tipos se pueden usar por separado o se pueden combinar en un solo sistema. Se puede realizar una función de transferencia de cables con la red que se muestra en la Figura 5.5. La función de transferencia de esta red es

\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{1}{\alpha} \left [\dfrac{\alpha \tau s + 1}{\tau s + 1} \right ] \nonumber \]

dónde\(\alpha = (R_1 + R_2)/R_2\) y\(\tau = (R_1 || R_2)C\). Como su nombre lo indica, esta red proporciona desplazamiento de fase positivo o principal de la señal de salida en relación con la señal de entrada en todas las frecuencias. Los parámetros de red de plomo generalmente se seleccionan para ubicar sus singularidades cerca de la frecuencia de cruce del sistema que se está compensando. El desplazamiento de fase positivo de la red mejora entonces el margen de fase del sistema. En muchos casos, la red principal tiene un efecto insignificante sobre las características de magnitud del sistema compensado a o por debajo de la frecuencia de cruce, ya que veremos que una red de leads proporciona un desplazamiento de fase sustancial antes de que su magnitud aumente significativamente.

Figura 5.6 Red de rezago.

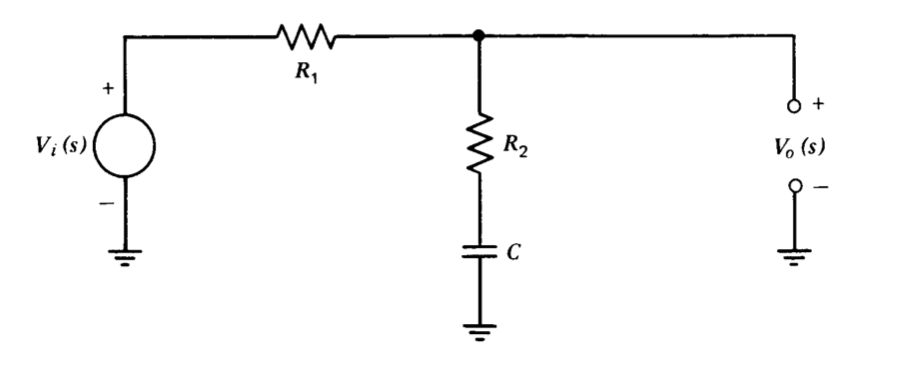
La red de retraso que se muestra en la Figura 5.6 tiene la función de transferencia

\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{\tau s + 1}{\alpha \tau s + 1} \nonumber \]

dónde\(\alpha = (R_1 + R_2)/R_2\) y\(\tau = R_2 C\). Las singularidades de este tipo de red suelen ubicarse muy por debajo del cruce para reducir la frecuencia de cruce de un sistema de manera que el desplazamiento de fase negativo asociado a otros elementos del sistema se reduzca a la frecuencia de unidad-ganancia. Este efecto es posible debido a la atenuación de la red lag a frecuencias por encima de sus dos singularidades.

La magnitud máxima del ángulo de fase asociado con cualquiera de estas funciones de transferencia es

\[\phi_{\max} = \sin^{-1} \left [\dfrac{\alpha - 1}{\alpha + 1} \right ] \nonumber \]

y esta magnitud ocurre en la media geométrica de las frecuencias de las dos singularidades. La ganancia de cualquiera de las redes a su frecuencia de desplazamiento de fase máxima es\(1/\sqrt{a}\).

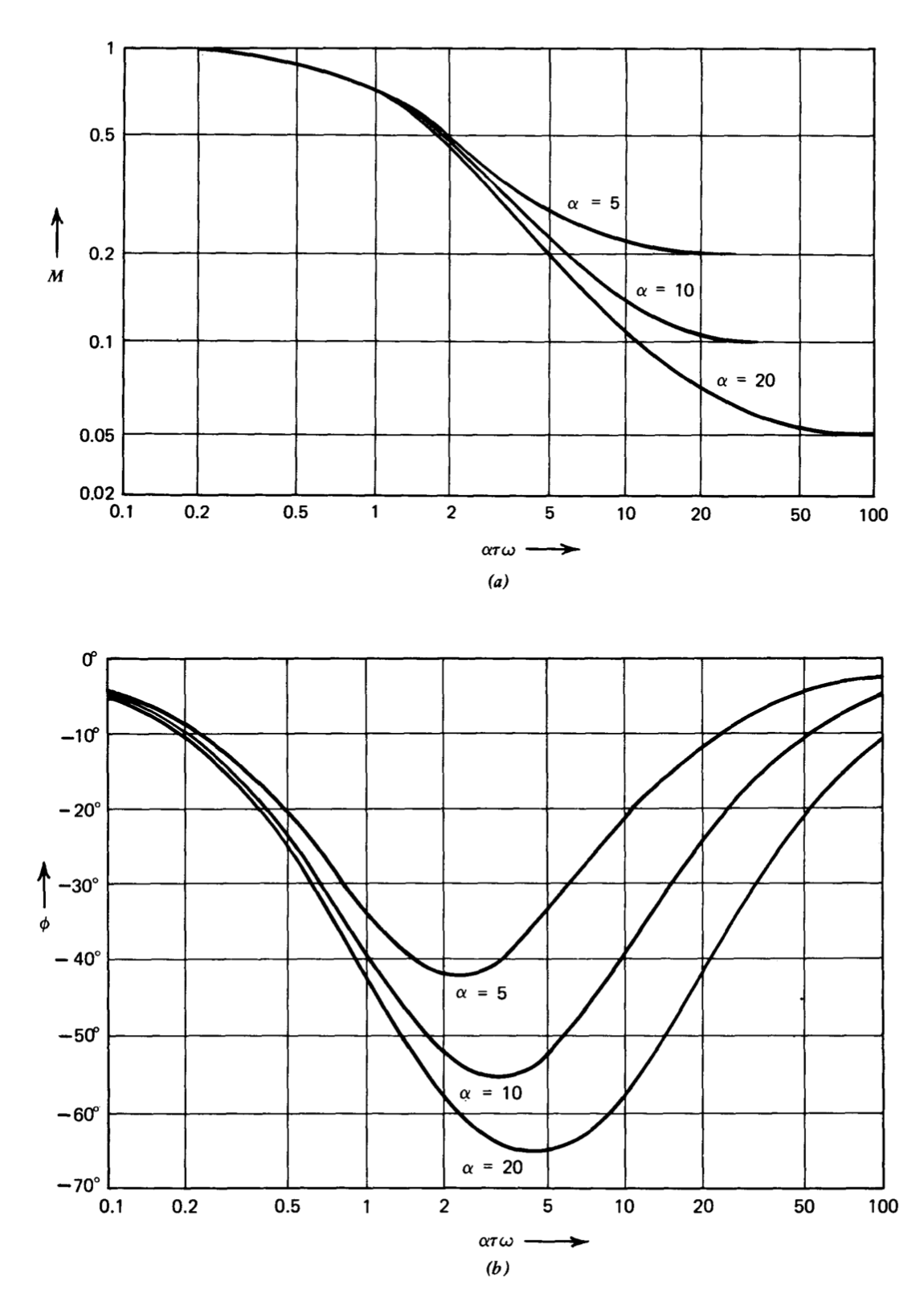
Las magnitudes y ángulos de las funciones de transferencia de plomo para\(\alpha\) valores de 5, 10 y 20, se muestran en forma de diagrama de Bodes en la Figura 5.7. La Figura 5.8 muestra las curvas correspondientes para las funciones de transferencia de retardo. Las frecuencias de esquina para

los polos de las funciones trazadas se normalizan a uno en estas figuras. Como se mencionó anteriormente, una característica importante de la función de transferencia de plomo es que proporciona un desplazamiento de fase positivo sustancial en un rango de frecuencias

por debajo de su ubicación cero sin un aumento significativo de magnitud. La razón deriva de una propiedad básica de las singularidades del eje real. En frecuencias por debajo de la ubicación cero, esta singularidad domina la función de transferencia de plomo, por lo que

\[\dfrac{V_o (s)}{V_i (s)} \simeq \dfrac{1}{\alpha} (\alpha \tau s + 1) \nonumber \]

La magnitud y el ángulo de esta función son

\[M = \dfrac{1}{\alpha} [\sqrt{1 + (\alpha \tau \omega)^2}] \nonumber \]

\[\phi = \tan^{-1} \alpha \tau \omega \nonumber \]

En una pequeña fracción de la ubicación cero,\(\alpha \tau \omega \ll 1\), entonces

\[M \simeq \dfrac{1}{\alpha} \left [1 + \dfrac{(\alpha \tau \omega)^2}{2} \right ] \nonumber \]

\[\phi \simeq \alpha \tau \omega \nonumber \]

Figura 5.7 Características de la red de plomo para\(V_o (s)/V_i (s) = (1/\alpha)[(\alpha \tau s + 1)/(\tau s + 1)]\). (\(a\)) Magnitud. (\(b\)) Ángulo.

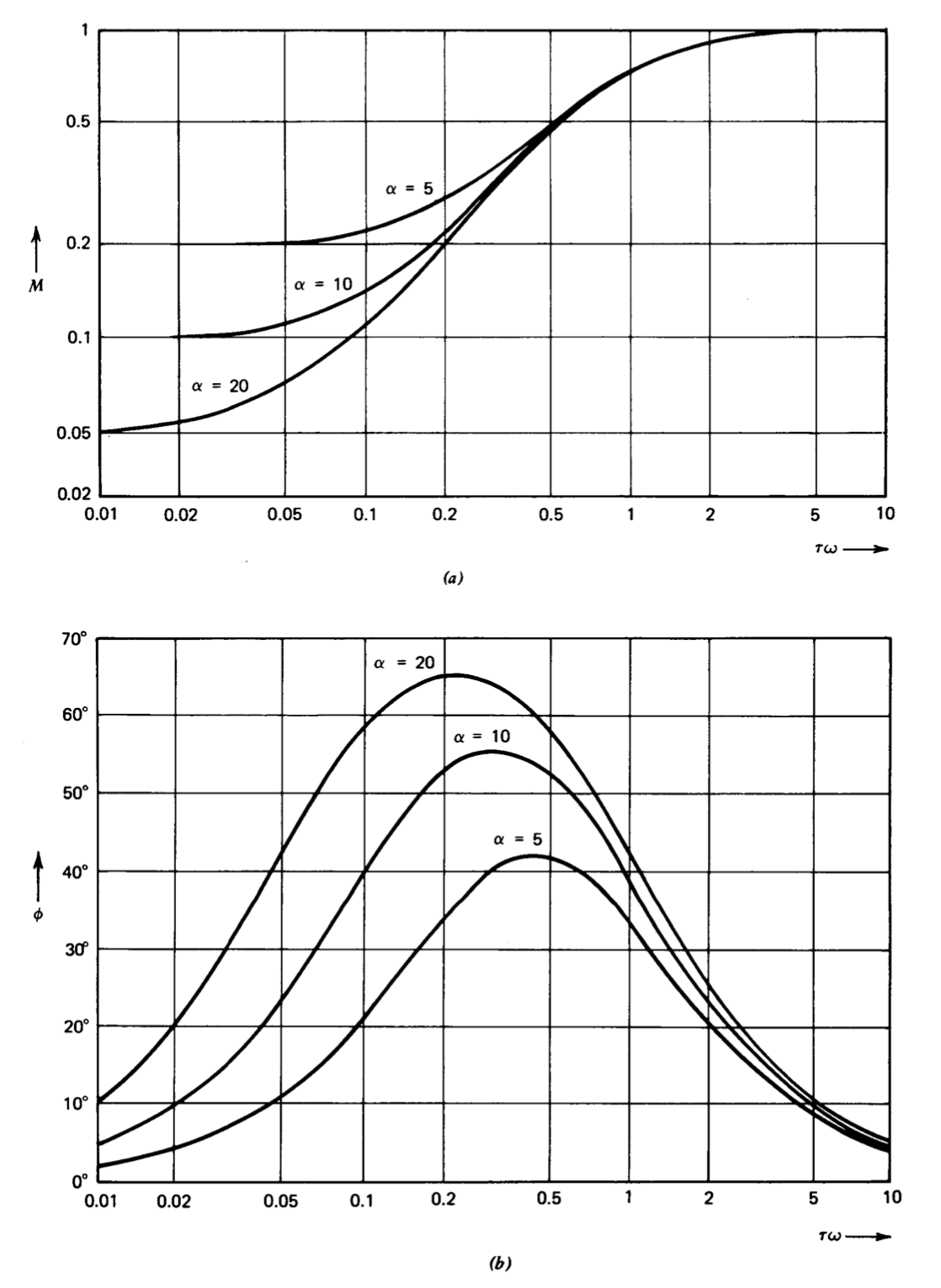
Dado que el ángulo aumenta linealmente con la frecuencia en esta región mientras que la magnitud aumenta cuadráticamente, el cambio de ángulo es relativamente mayor a una frecuencia dada. El mismo tipo de razonamiento se aplica incluso si el cero se ubica en o ligeramente por debajo del cruce. La Figura 5.7 muestra que el desplazamiento de fase positivo de una función de transferencia de leads con un valor razonable de\(\alpha\) se encuentra aproximadamente\(40^{\circ}\) en su ubicación cero, mientras que el incremento de magnitud es solo un factor de 1.4. Gran parte de esta ventaja se pierde en frecuencias más allá de la media geométrica de las singularidades, ya que el desplazamiento de fase positivo disminuye más allá de esta frecuencia, mientras que la magnitud sigue aumentando.

Figura 5.8 Características de la red de retardo para\(V_o (s)/V_i (s) = (\tau s + 1)/(\alpha \tau s + 1)\). (\(a\)) Magnitud. (\(b\)) Ángulo.

Debemos reconocer que se puede usar un cero aislado en lugar de una función de transferencia de plomo, y que este tipo de función de transferencia en realidad tiene características de cambio de fase superiores a las del par de polos cero. Sin embargo, la ganancia ilimitada de alta frecuencia implicada por un cero aislado es claramente inalcanzable, al menos a frecuencias suficientemente altas. Así, la forma de la función de transferencia de plomo introducida anteriormente refleja las realidades de los sistemas físicos.

La característica importante de la función de transferencia de retardo ilustrada en la Figura 5.8 es que a frecuencias muy por encima de la ubicación cero, proporciona una atenuación de magnitud igual a la relación de las dos ubicaciones de singularidad y desfase insignificante. Por lo tanto, se puede utilizar para reducir la magnitud de la transmisión de bucle sin agregar significativamente al desplazamiento de fase negativo de esta transmisión a frecuencias moderadas.

Ejemplo

Figura 5.9 Amplificador de ganancia de diez.

Las redes de plomo y lag se desarrollaron originalmente para su uso en anismos servomech, y proporcionan un poderoso medio de compensación cuando sus singularidades pueden ubicarse arbitrariamente con respecto a otros polos del sistema y cuando es posible un ajuste independiente de la magnitud de transmisión de bucle de baja frecuencia. Incluso sin esta flexibilidad, que generalmente está ausente con los circuitos de amplificador operativo, la compensación de plomo o retraso puede proporcionar un control efectivo del rendimiento de bucle cerrado en ciertas configuraciones. Como ejemplo, considere la conexión de amplificador no inversora de ganancia de diez que se muestra en la Figura 5.9. Se supone que la admitancia de entrada y la impedancia de salida del amplificador operacional son pequeñas. La función de transferencia de bucle abierto del amplificador operacional es (Si bien\(a(s)\) en este ejemplo se usa una expresión analítica, el lector debe darse cuenta de que la función de transferencia de bucle abierto de un amplificador operacional generalmente no estará disponible en esta forma. Tenga en cuenta, sin embargo, que una gráfica de Bode determinada experimentalmente es completamente aceptable para todas las manipulaciones requeridas, y que esta información siempre se puede determinar. Las características generales de la supuesta función de transferencia de bucle abierto son típicas de muchos amplificadores operativos, ya que esta cantidad está dominada por un solo polo a bajas frecuencias. A frecuencias más cercanas a la frecuencia de ganancia unitaria, el desplazamiento de fase negativo adicional resulta de efectos relacionados con limitaciones de transistores. Como veremos en secciones posteriores, estos efectos limitan las últimas capacidades de rendimiento del amplificador).

\[a(s) = \dfrac{5 \times 10^5}{(s + 1)(10^{-4} s + 1) (10^{-5} s + 1)} \nonumber \]

y se supone que el usuario no puede alterar esta función. Cuando se conecta como se muestra en la Figura 5.9 el valor de\(f\) es 0.1, y por lo tanto el negativo de la transmisión en bucle es

\[a(s)f(s) = \dfrac{5 \times 10^4}{(s + 1)(10^{-4} s + 1) (10^{-5} s + 1)}\label{eq5.2.11} \]

La ganancia de bucle cerrado es

\[\begin{array} {rcl} {\dfrac{V_o (s)}{V_i (s)} = A(s)} & = & {\dfrac{a(s)}{1 + a(s) f(s)}} \\ {} & \simeq & {\dfrac{10}{2 \times 10^{-14} s^3 + 2.2 \times 10^{-9} s^2 + 2 \times 10^{-5} s + 1}} \end{array} \nonumber \]

Figura 5.10 Gráfica de Bode para amplificador de grano de diez no compensado. \(af = 5 \times 10^4/[(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)]\).

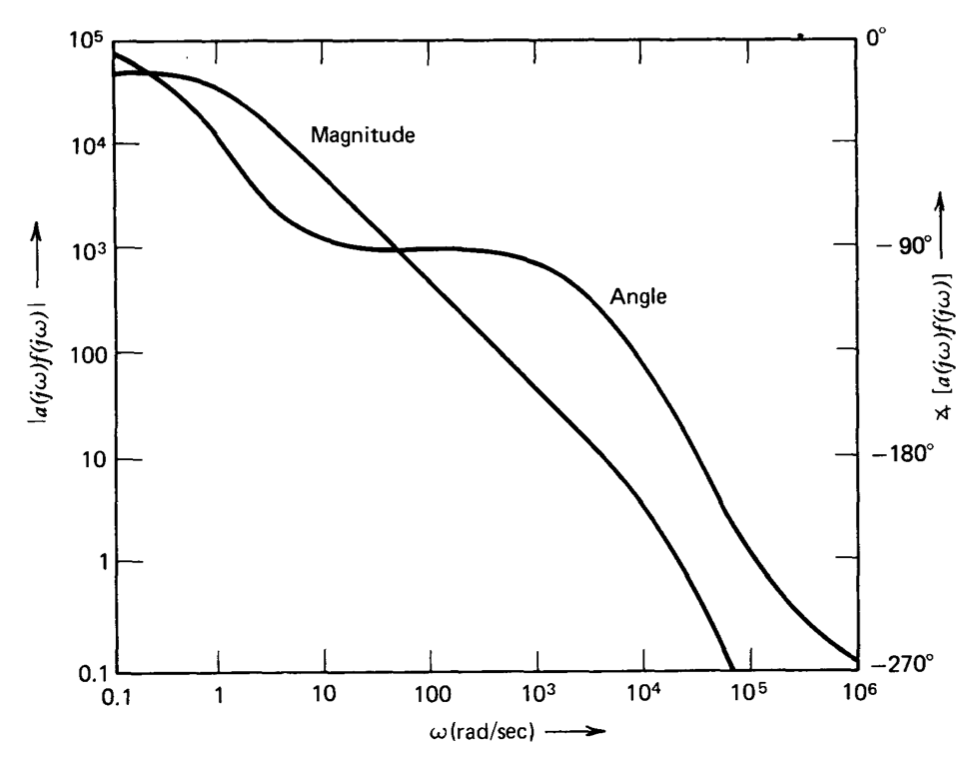
Una gráfica de Bode de la Ecuación\(\ref{eq5.2.11}\) (Figura 5.10) muestra que la frecuencia de cruce del sistema es\(2.1 \times 10^4\) radianes por segundo, su margen de fase es\(13^{\circ}\) y el margen de ganancia es 2.

Figura 5.11 Amplificador de ganancia de diez con red de conductores en ruta de retroalimentación. (\(a\)) Circuito. (\(b\)) Diagrama de bloques.

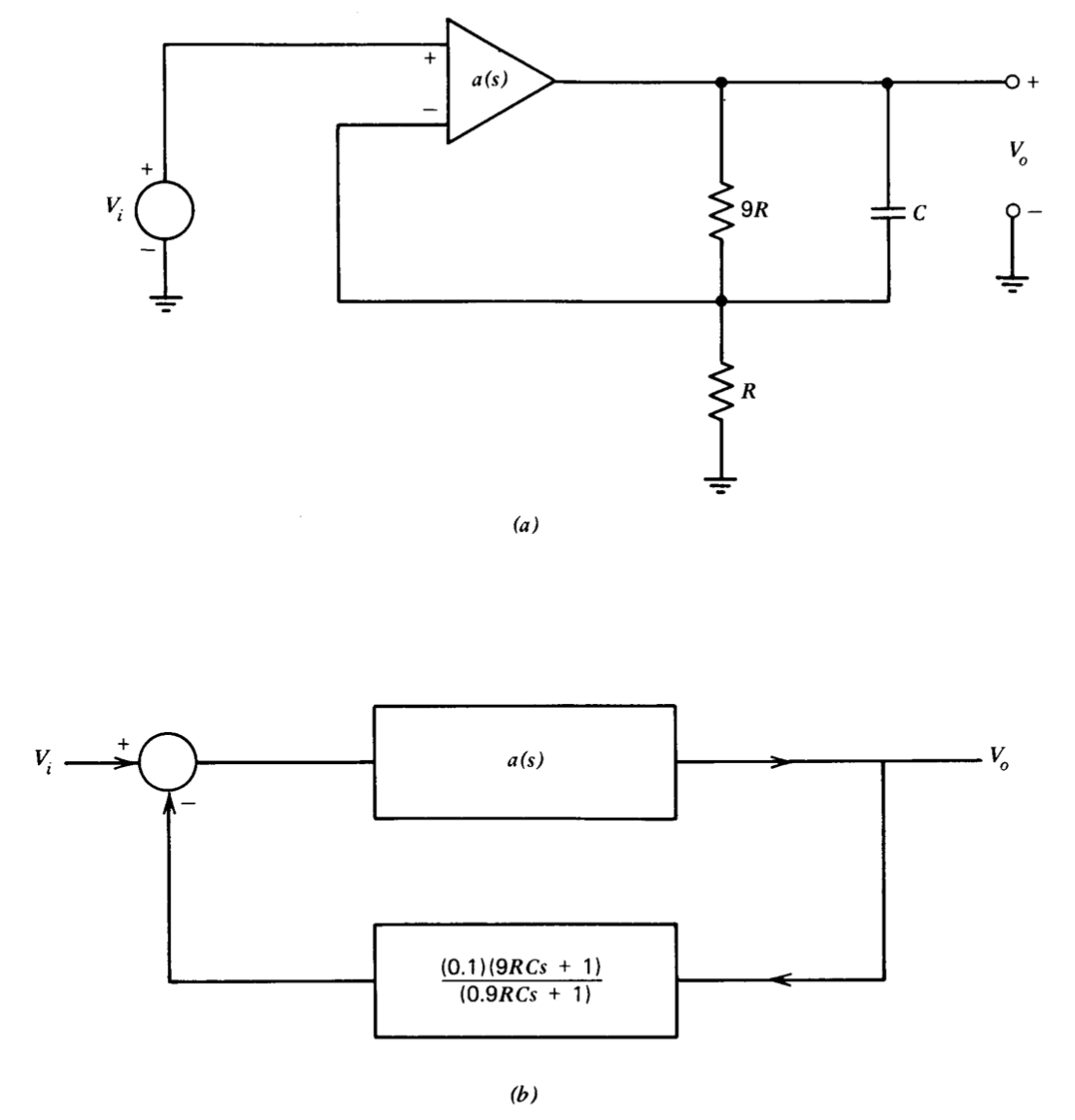
Si bien la declaración del problema impide la alteración\(a(s)\), podemos introducir una función de transferencia de cables en la transmisión de bucle al incluir un condensador a través de la resistencia superior en la red de retroalimentación. La topología se muestra en la Figura 5.11\(a\), con un diagrama de bloques mostrado en la Figura 5.11\(b\). El negativo de la transmisión en bucle para el sistema es

\[a'(s) f'(s) = \dfrac{5 \times 10^4 (9RCs + 1)}{(s + 1)(10^{-4}s + 1)(10^{-5} s + 1)(0.9 RCs + 1)}\label{eq5.2.13} \]

Varias consideraciones influyen en la selección del\(R-C\) producto que localiza las singularidades de la red de leads. Como se mencionó anteriormente, el objetivo de una red principal es proporcionar un desplazamiento de fase positivo en las proximidades de la frecuencia de cruce, y el desplazamiento de fase positivo máximo de los resultados de la red si el cruce ocurre en la media geométrica del par de polos cero. Sin embargo, las singularidades de la red y el cruce frecuentemente no se pueden ajustar independientemente para este sistema, ya que si el cero de la red principal se ubica a una frecuencia por debajo de aproximadamente\(3 \times 10^4\) radianes por segundo, la frecuencia de cruce aumenta. Un aumento en la frecuencia de cruce aumenta el desplazamiento de fase negativo del amplificador a esta frecuencia, compensando en parte el desplazamiento de fase positivo de la red. Una consideración relacionada implica el efecto de la red principal en la ganancia ideal de bucle cerrado del amplificador ya que la red se introduce en la ruta de retroalimentación y la ganancia ideal está relacionada recíprocamente con la función de transferencia de retroalimentación. Si el cero de la red principal se encuentra en una frecuencia baja, resulta un polo de bucle cerrado de baja frecuencia que reduce el ancho de banda de bucle cerrado del sistema.

Figura 5.12 Gráfica de Bode para amplificador de ganancia de diez compensado por plomo. \(a'f' = 5 \times 10^4 (4 \times 10^{-5}s + 1)/[(s+1)(10^{-4} s + 1) (10^{-5} s + 1) (4 \times 10^{-6} s + 1)]\).

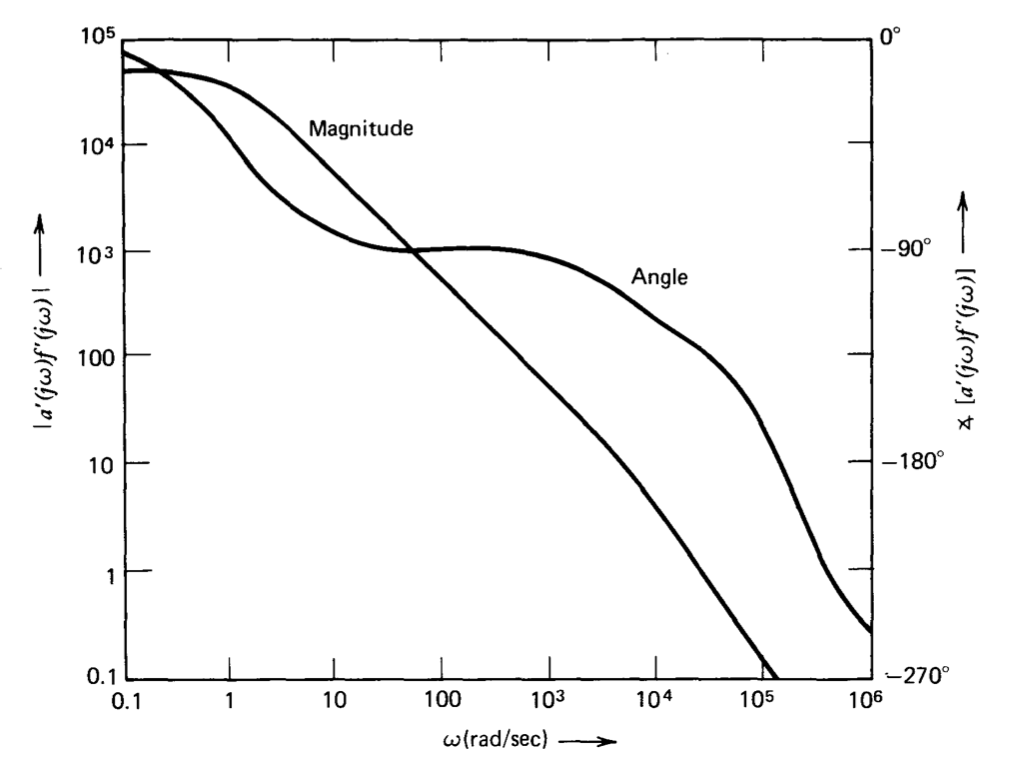
Un compromiso razonable en este caso es ubicar el cero de la red principal cerca de la frecuencia de ganancia unitaria, en un intento de obtener un desplazamiento de fase positivo de la red sin un aumento significativo en la frecuencia de cruce. Los\(RC = 4.44 \times 10^{-6}\) segundos de elección localizan el cero en\(2.5 \times 10^4\) radianes por segundo. Una gráfica Bode de Ecuación\(\ref{eq5.2.13}\) para este valor de RC se muestra en la Figura 5.12. La frecuencia de ganancia unitaria se incrementa ligeramente a\(2.5 \times 10^4\) radianes por segundo, mientras que el margen de fase se incrementa al valor respetable de\(47^{\circ}\). El margen de ganancia es 14.

Se puede introducir una función de transferencia de retardo en la trayectoria directa del amplificador derivando una red de resistencia-condensador en serie entre sus terminales de entrada como se muestra en la Figura 5.13\(a\). Tenga en cuenta que la misma transmisión de bucle podría obtenerse derivando la resistencia con valor R con la\(R_1 -C\) red, ya que tanto el extremo inferior de la resistencia\(R\) valorada como la entrada no inversora del amplificador están conectados a puntos de conexión a tierra incrementalmente. Si se utilizara esta opción posterior, la\(R_1-C\) red introduciría la función de transferencia de retardo en la ruta de retroalimentación de la topología. En consecuencia, la función de transferencia de bucle cerrado ideal incluiría el recíproco de la función de retardo. Dado que las singularidades de las redes de retardo generalmente se ubican a bajas frecuencias, la función de transferencia de bucle cerrado podría verse afectada negativamente en las frecuencias de interés. (Ver Problema P5.7.)

Figura 5.13 Amplificador de ganancia de diez con compensación de lag. (\(a\)) Circuito. (\(b\)) Diagrama de bloques. (\(c\)) Diagrama de bloques después del reordenamiento.

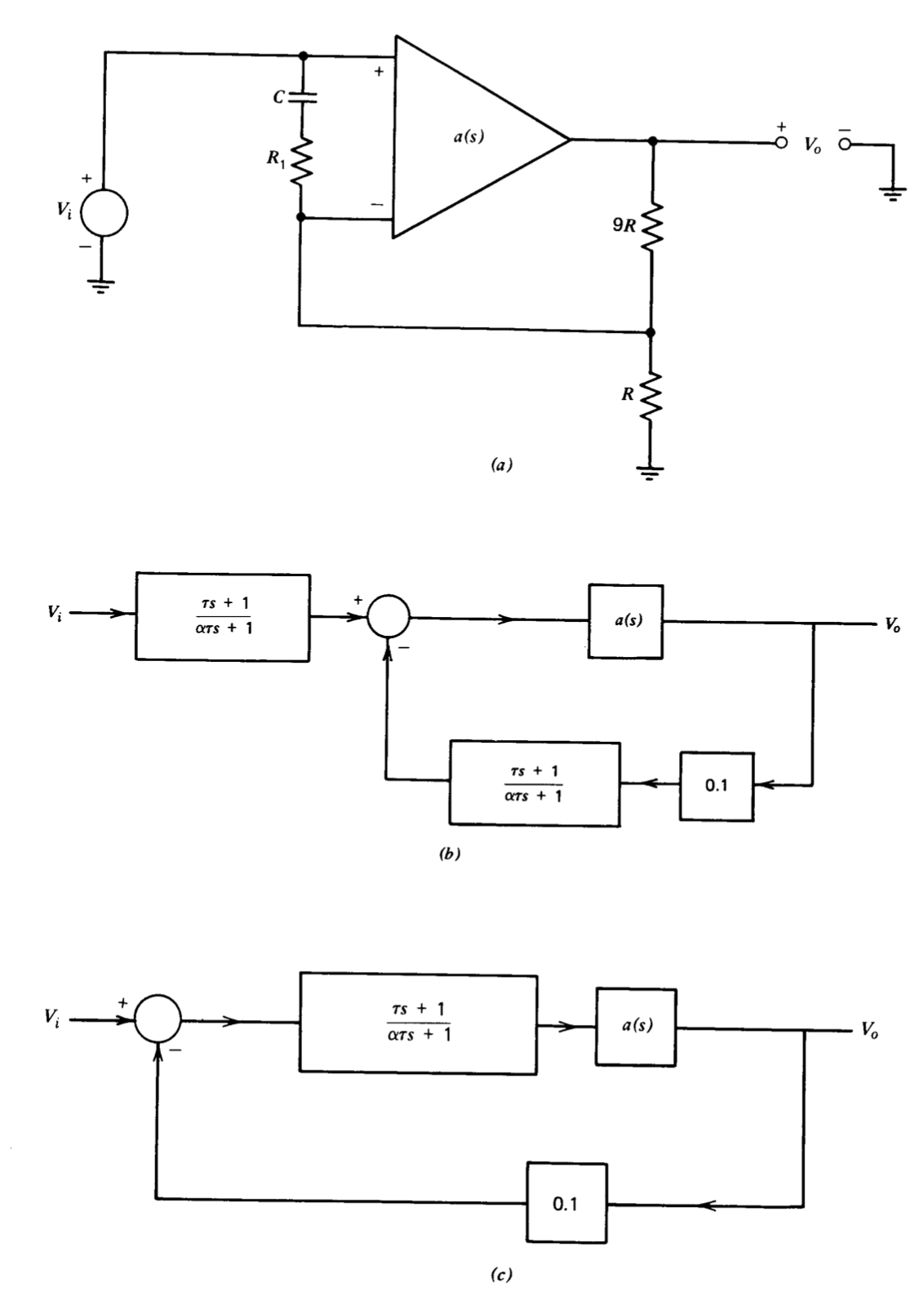
El diagrama de bloques del sistema para la topología de la Figura 5.13\(a\) se muestra en la Figura 5.13\(b\). En este caso, la función de transferencia de retardo aparece tanto en la ruta de retroalimentación como en una ruta de avance fuera del bucle. El diagrama de bloques se puede reorganizar como se muestra en la Figura 5.13\(c\); y este diagrama final muestra que incluir la\(R_1-C\) red entre las entradas del amplificador deja sin cambios la ganancia ideal de bucle cerrado. El negativo de la transmisión en bucle para la Figura 5.13\(c\) es

\[a''(s) f''(s) = 0.1 \dfrac{(\tau s + 1)}{(\alpha \tau s + 1)} a(s) \nonumber \]

donde

\[\alpha = \dfrac{R_1 + 0.9 R}{R_1} \text{ and } \tau = R_1 C\nonumber \]

Como se mencionó anteriormente, las singularidades de una función de transferencia de retardo generalmente se ubican muy por debajo de la frecuencia de cruce del sistema para que la red de retardo no deteriore el margen de fase significativamente. Una regla general de uso frecuente sugiere ubicar el cero de la red de retardo en una décima parte de la frecuencia de cruce que resulta después de la compensación, ya que este valor produce una contribución de fase negativa máxima\(5.7^{\circ}\) de la red en el cruce. También, de manera bastante arbitraria, decidimos elegir los parámetros de red retardada para obtener un margen de fase de aproximadamente\(47^{\circ}\), el mismo valor que el del sistema compensado con una red de plomo. La gráfica Bode del sistema sin compensación, Figura 5.10, ayuda en la selección de parámetros de redes rezagadas. Esta gráfica indica un ángulo de fase no compensado de\(-128^{\circ}\) y una magnitud no compensada de 6.2 a una frecuencia de\(6.7 \times 10^3\) radianes por segundo. Si el valor de 6.2 es la atenuación de alta frecuencia elegida a de la red de retardo, la frecuencia de cruce compensada será\(6.7 \times 10^3\) radianes por segundo. El desplazamiento\(5^{\circ}\) de fase negativo anticipado de una red de lag correctamente ubicada se combina con el desplazamiento\(- 128^{\circ}\) de fase del sistema previo a la compensación para producir un margen de fase compensado de\(47^{\circ}\). El cero de la red de rezago se ubica en\(6.7 \times 10^2\) radianes por segundo, un factor 10 por debajo del cruce. Estos objetivos de diseño se cumplen con\(R_1 = 0.173R\) y\(R_1C = 1.5 \times 10^{-3}\) segundos. Con estos valores, el negativo de la transmisión en bucle es

\[a''(s) f''(s) = \dfrac{5 \times 10^4 (1.5 \times 10^{-3} s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(9.3 \times 10^{-3} s + 1)} \nonumber \]

Figura 5.14 Gráfica de Bode para amplificador de ganancia de diez compensado por lag. \(a'' f'' = 5 \times 10^4 (1.5 \times 10^{-3} s + 1)/[(s + 1)(10^{-4} s + 1)(10^{-5}s + 1)(9.3 \times 10^{-3} s + 1)]\).

Esta función de transferencia, trazada en la Figura 5.14, indica valores predichos para frecuencia de cruce y margen de fase. El margen de ganancia es de 15.

Otras dos modificaciones de la transmisión en bucle dan como resultado gráficas de Bode que son similares a las del sistema con retraso compensado en las proximidades de la frecuencia de cruce. Una posibilidad es bajar el valor\(a_0f_0\) de en un factor de 6.2 (ver Sección 5.2.1). La reducción requerida se puede lograr simplemente usando el valor de resistencia de derivación determinado para la compensación de retardo directamente a través de los terminales de entrada del amplificador operativo. Esta modificación da como resultado la misma frecuencia de cruce que la del amplificador lag-compen sated, y tiene varios grados más de margen de fase ya que no tiene el ligero desplazamiento de fase negativo asociado con la red de lag en el cruce. Desafortunadamente, la disminución\(a_0f_0\) da como resultado un menor valor para la desensitividad en comparación con el del amplificador con retraso compensado en todas las frecuencias por debajo del cero de la red.

Una segunda posibilidad es mover el polo de menor frecuencia de la transmisión de bucle de vuelta por un factor de 6.2. Esta modificación podría hacerse en el propio amplificador, o podría lograrse mediante la selección apropiada de componentes de red retardada. El efecto sobre los parámetros en las proximidades del cruce es esencialmente idéntico al de la reducción\(a_0f_0\). La desensitividad se retiene en d-c con este método, pero se reduce a frecuencias intermedias en comparación con la proporcionada por la compensación de lag. Estos dos enfoques para compensar el amplificador descrito aquí se investigan en detalle en el Problema P5.8.

Figura 5.15 Diagramas de locus raíz que ilustran la compensación de ganancia de diez ampli fier. (\(a\)) No compensado. (\(b\)) Plomo compensado. (\(c\)) Retraso compensado.

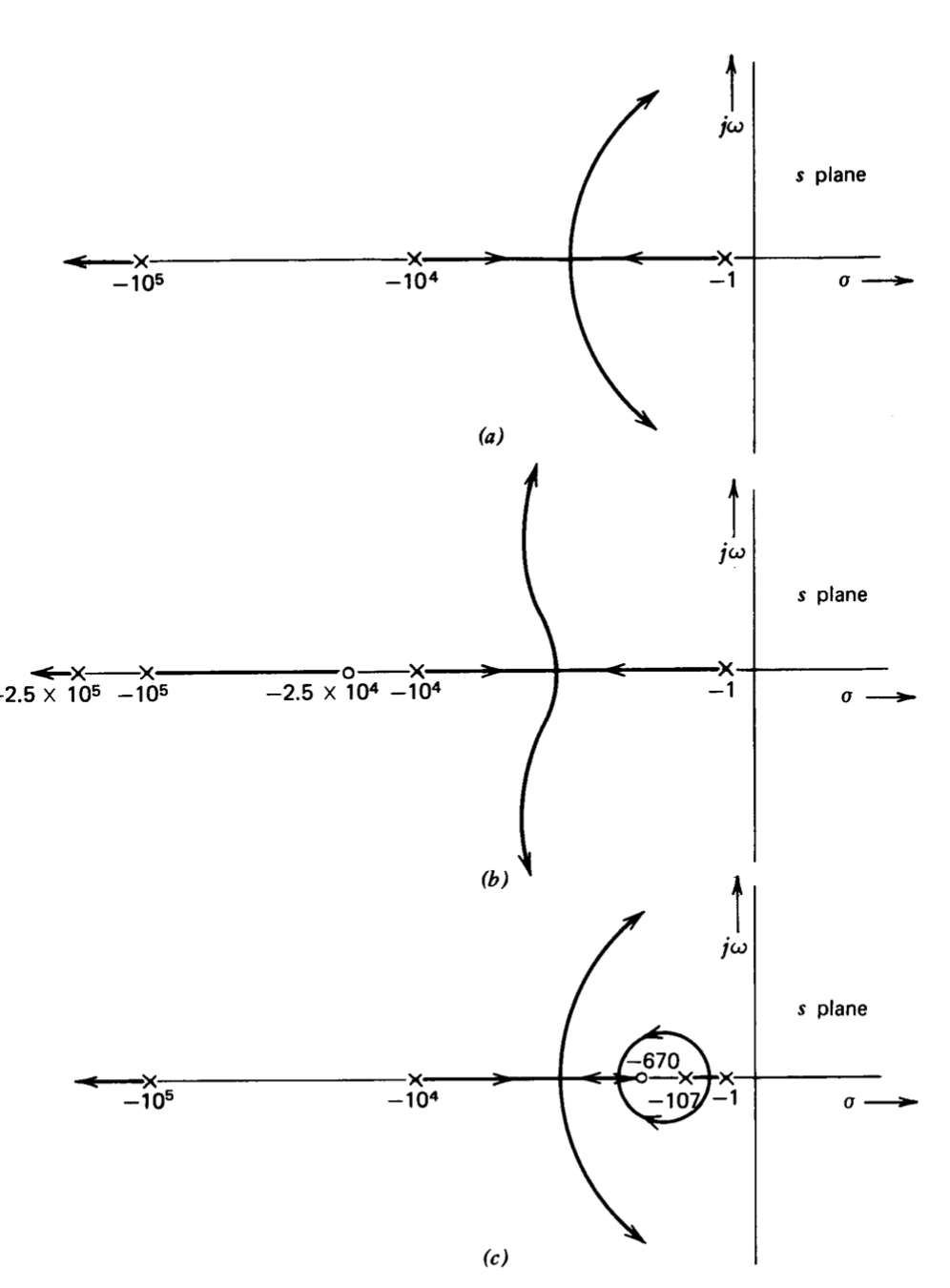
La discusión de la compensación de series hasta este punto se ha centrado en el uso de los conceptos de dominio de frecuencia de margen de fase, margen de ganancia y frecuencia de cruce para determinar parámetros de red de compensación. Los métodos de locus raíz no se pueden usar directamente ya que el valor\(a_0f_0\) de no varía para efectuar la compensación. Sin embargo, los bocetos de locus raíz para los sistemas no compensados, compensados por plomo y retardados mostrados en la Figura 5.15 dan un grado de comprensión del comportamiento del sistema. (Hay distorsión significativa en estos bocetos, ya que no es conveniente presentar bocetos con precisión donde las singularidades se ubican con varias décadas de diferencia).

El diagrama de locus raíz de la Figura 5.15\(a\) ilustra el cambio en la ubicación de los polos de bucle cerrado como una función de\(a_0f_0\) para el sistema no compensado. Sumando la red de plomo (Figura 5.15\(b\)) desplaza las ramas dominantes hacia la izquierda y, así, mejora la relación de amortiguación de este par de polos para un valor dado de\(a_0f_0\).

El efecto de la compensación de retraso es algo más sutil. El diagrama raíz-locus de la Figura 5.15\(c\) es prácticamente idéntico al de la Figura 5.15\(a\) excepto en las inmediaciones del par de singularidad de red retardada. Sin embargo, un cálculo de ganancia usando la regla 8 (Sección 4.3.1) muestra que el valor de\(a_0f_0\) requerido para alcanzar una relación de amortiguación dada para el par dominante es mayor en aproximadamente un factor de a cuando se incluye la red de retraso.

Los contornos de raíz también se pueden usar para mostrar los efectos de variar un solo parámetro de la red lead o lag. Este enfoque de diseño se explora en Problemas P5.9 y P5.10.

Evaluación de los Efectos de la Compensación

Existen varias formas de demostrar la mejora en el desempeño que brinda la compensación. Dado que los parámetros de la función de transferencia compensadora generalmente se determinan con la ayuda de gráficos Bode de transmisión en bucle, una manera sencilla de evaluar varios tipos de compensación es comparar la desensitividad obtenida de ellos. Las consideraciones utilizadas para determinar los parámetros de compensación de plomo y retardo para un amplificador operacional conectado para proporcionar una ganancia de 10 se describieron en detalle en la Sección 5.2.4. Las transmisiones de bucle resultantes, que se repiten aquí por conveniencia, son

\[a'(s) f'(s) = \dfrac{5 \times 10^4 (4 \times 10^{-5} s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(4 \times 10^{-6} s + 1)}\label{eq5.2.16} \]

y

\[a''(s) f''(s) = \dfrac{5 \times 10^4 (1.5 \times 10^{-3} s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(9.3 \times 10^{-3} s + 1)}\label{eq5.2.17} \]

para los casos compensados por plomo y retraso, respectivamente. El margen de fase obtenido por cualquiera de los dos métodos es aproximadamente\(47^{\circ}\).

Se mencionó que la estabilidad del amplificador no compensado podría mejorarse ya sea\(a_0f_0\) bajando en un factor de 6.2, resultando en

\[a''' (s) f(s)''' = \dfrac{8.1 \times 10^3}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)} \nonumber \]

o bajando la ubicación del primer polo por el mismo factor, cediendo

\[a'''' (s) f''''(s) = \dfrac{5 \times 10^4}{(6.2 s + 1)(10^{-4} s + 1)(10^{-5} s + 1)} \nonumber \]

Cualquiera de estos enfoques da como resultado una frecuencia de cruce idéntica a la del sistema con retraso compensado y un margen de fase de aproximadamente\(52^{\circ}\).

Figura 5.16 Efectos de varios tipos de compensación sobre la magnitud de transmisión de bucle.

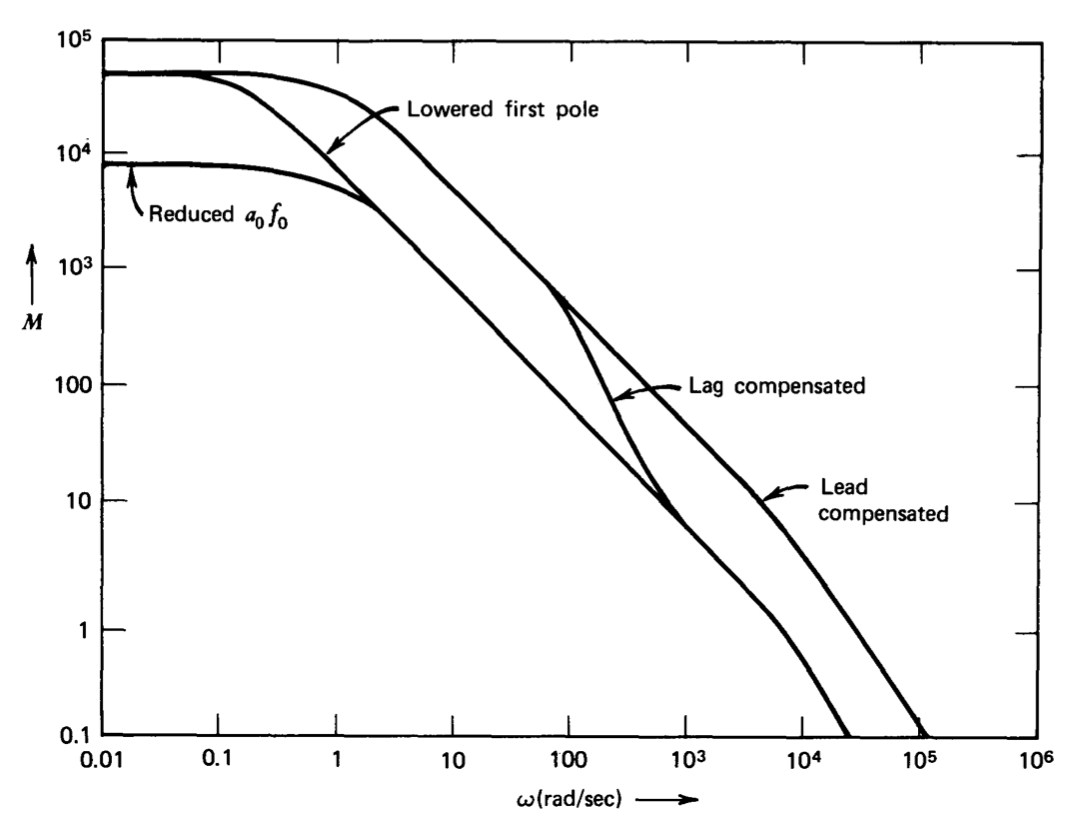
Las porciones de magnitud de las transmisiones de bucle para estos cuatro casos se comparan en la Figura 5.16. Las desensibilidades relativas que se logran a diversas frecuencias, así como las frecuencias de cruce relativas, son evidentes en esta figura.

Una forma alternativa de evaluar diversas técnicas de compensación es comparar los coeficientes de error que se obtienen utilizando las mismas. Este enfoque se explora en el Problema P5.11. Como era de esperar, los sistemas con mayor desensitividad generalmente también tienen coeficientes de error de menor magnitud.

La discusión de la compensación hasta ahora se ha centrado en el uso de parcelas Bode, ya que esta suele ser la forma más rápida de encontrar parámetros compensadores. Sin embargo, los objetivos de diseño se establecen con frecuencia en términos de respuesta transitoria, y el diseñador inexperto a menudo siente que se requiere un acto de fe para aceptar el principio de que los sistemas con valores adecuadamente elegidos para el margen de fase, el margen de ganancia y la frecuencia de cruce producirán transitorios satisfactorios respuestas. Las respuestas escalonadas mostradas en la Figura 5.17 se ofrecen como una ayuda para establecer esta fe necesaria.

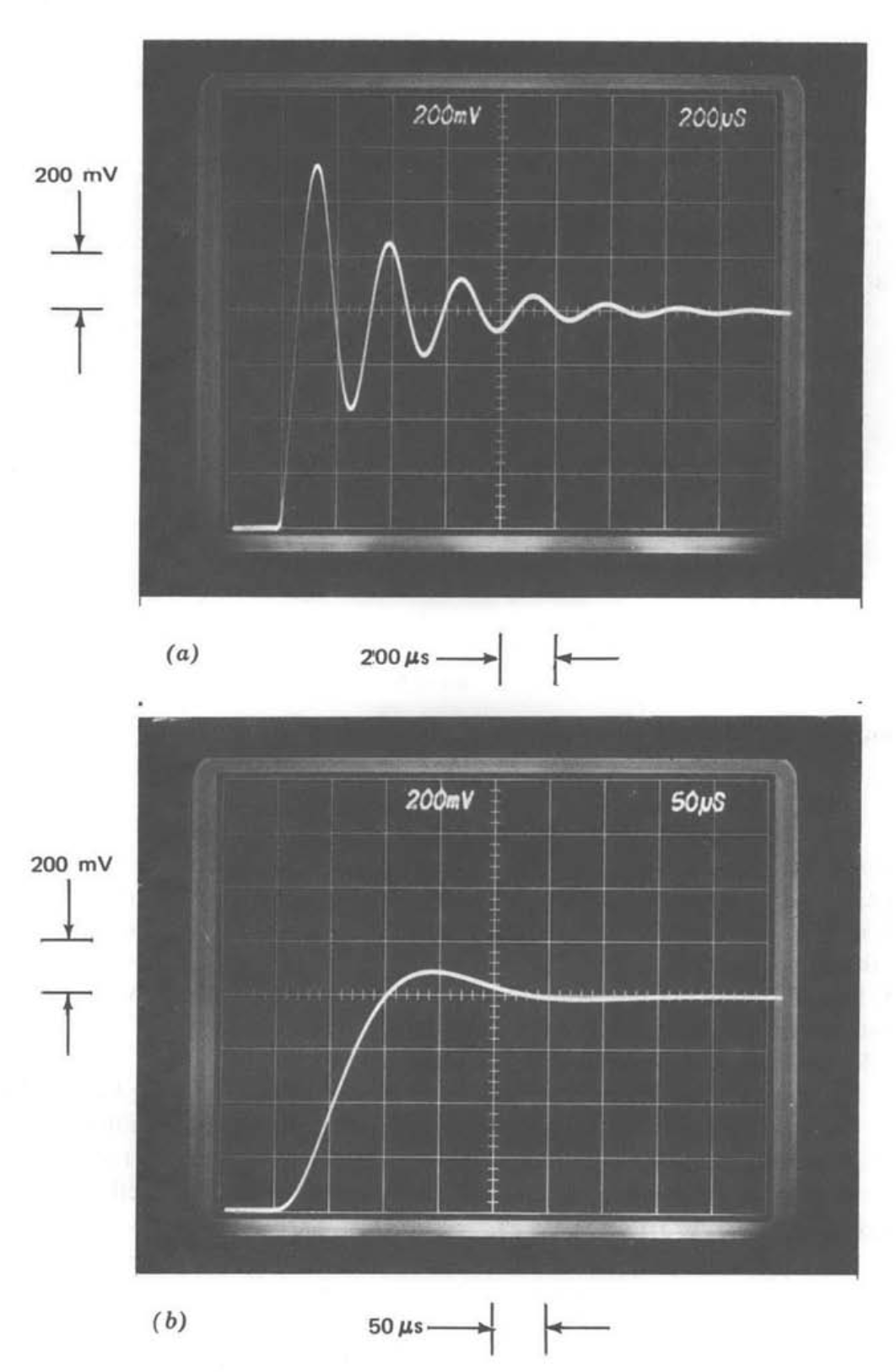
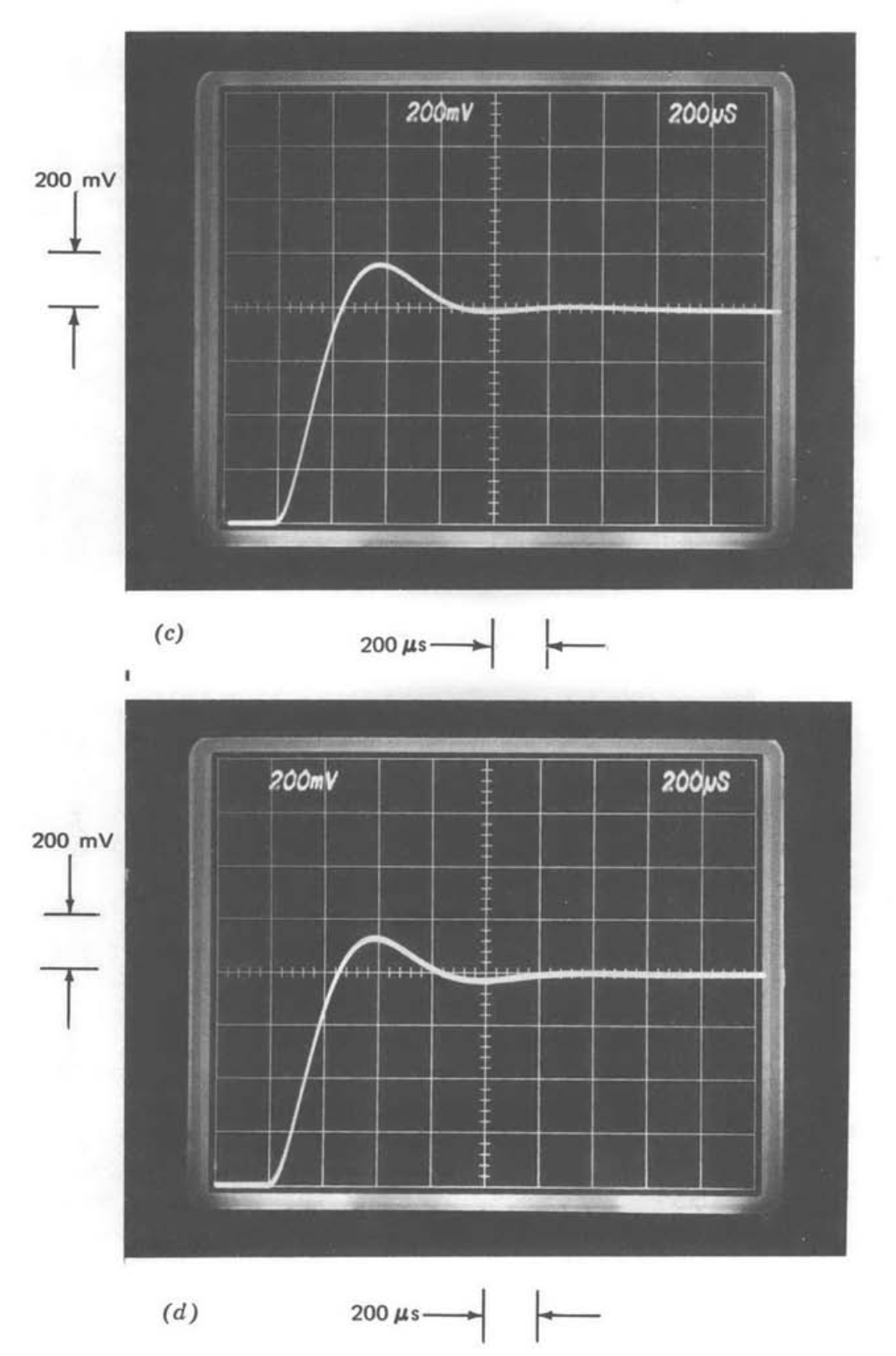
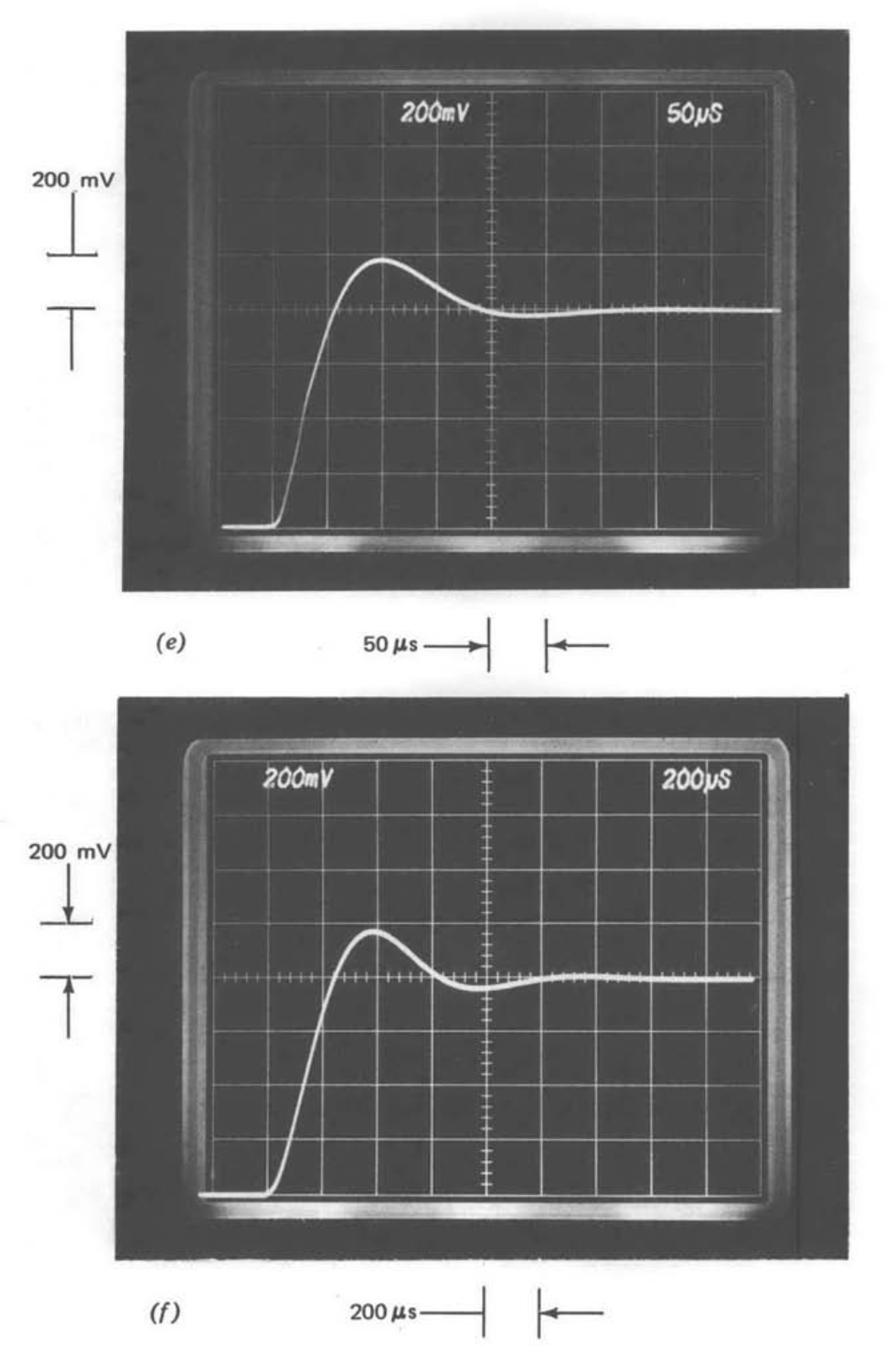
Figura 5.17 Respuesta del amplificador de ganancia de diez a un paso de 80 mV. (\(a\)) No hay compensación. (\(b\)) Plomo compensado. (\(c\)) Retraso compensado. (\(d\)) Rebajado\(a_0 f_0\). (\(e\)) Compensación de plomo en el camino de avance. (\(f\)) Aproximación de segundo orden a (\(c\)).

La Figura 5.17\(a\) muestra la respuesta escalonada del amplificador de ganancia de diez sin compensación. El sobreimpulso de pico grande y la mala amortiguación del timbre reflejan el bajo margen de fase del sistema. El sobreimpulso y la amortiguación para los\(a_0f_0\) casos compensados de plomo, compensados por lag y reducidos (Figs. 5.17\(b\), 5.17\(c\) y 5.17\(d\), respectivamente) se mejoran significativamente, como se anticipó en vista de los márgenes de fase mucho más altos de estas conexiones. No se muestra la respuesta escalonada obtenida al bajar la frecuencia del primer polo en el bucle, ya que es indistinguible de la Figura 5.17\(d\).

Ciertas características de estas respuestas escalonadas son evidentes a partir de las cifras. El sobreimpulso máximo exhibido por el amplificador con reducción\(a_0f_0\) es ligeramente menor que el del amplificador con compensación de lag, reflejando un margen de fase ligeramente superior. De igual manera, el tiempo de subida del amplificador con retardo compensado es muy ligeramente más rápido, reflejando nuevamente la influencia del margen de fase relativo en el rendimiento de estos dos sistemas con frecuencias de cruce idénticas. El sobreimpulso de pico más pequeño del sistema compensado por plomo no implica una mayor estabilidad relativa para este amplificador, sino que ocurre debido a la influencia de la red de conductores en la ruta de retroalimentación sobre la ganancia ideal de bucle cerrado.

La Figura 5.17\(e\) muestra la respuesta de paso que resulta si la compensación de plomo se proporciona en la ruta de avance en lugar de en la ruta de retroalimentación. Así, la transmisión en bucle para esta respuesta transitoria es idéntica a la de la Figura 5.17\(b\) (Ecuación\(\ref{eq5.2.16}\)), pero la ruta de retroalimentación para el sistema ilustrado en la Figura 5.17\(e\) es independiente de la frecuencia. Si bien la compensación de plomo de ruta de avance estaba prohibida por la declaración de problemas de los ejemplos anteriores, la Figura 5.17\(e\) proporciona una indicación más realista de estabilidad relativa que la Figura 5.17\(b\), ya que la Figura 5.17\(e\) se obtiene de un sistema con una ganancia ideal independiente de la frecuencia. La diferencia entre estos dos sistemas con transmisiones de bucle idéntico surge debido a diferencias en las ubicaciones cero de bucle cerrado (ver Sección 4.3.4).

El sobreimpulso máximo y la amortiguación relativa de las figuras 5.17\(c\) y 5.17\(e\) son prácticamente idénticos, lo que demuestra que, al menos para este ejemplo, valores iguales de margen de fase dan como resultado una estabilidad relativa igual para los sistemas compensados por plomo y retraso. El tiempo de subida de la Figura 5.17\(e\) es aproximadamente una cuarta parte del de la Figura 5.17\(c\), y esta relación es prácticamente idéntica a la relación de las frecuencias de cruce de los dos amplificadores.

La respuesta escalonada de la Figura 5.17\(f\) es la de un sistema de segundo orden con\(\zeta = 0.45\) y\(\omega_n = 8.5 \times 10^3\) radianes por segundo. Estos valores se obtuvieron utilizando la Figura 4.26\(a\) para determinar un sistema de aproximación de segundo orden al amplificador con retardo compensado. La similitud de las figuras 5.17\(c\) y 5.17\(f\) es otro ejemplo de la precisión que se obtiene frecuentemente cuando los sistemas complejos son aproximados por sistemas de primer o segundo orden. La transmisión en bucle para el sistema de retardo compensado (Ecuación\(\ref{eq5.2.17}\)) incluye cuatro polos y uno cero. Sin embargo, esta cantidad solo tiene un balanceo unipolar entre\(6.7 \times 10^2\) radianes por segundo y la frecuencia de cruce, con un segundo polo cerca del cruce. Así, se puede aproximar bien como un sistema con dos polos ampliamente separados, el modelo a partir del cual se desarrolló la Figura 4.26.

Consideraciones relacionadas

Varios comentarios adicionales sobre los beneficios relativos de los diferentes métodos de compensación en serie están en regla. La evaluación del desempeño en el ejemplo anterior parece implicar ventajas para la compensación de plomo. El amplificador compensado por plomo parece superior si la desensitividad a diversas frecuencias, magnitud de coeficiente de error o velocidad de respuesta transitoria es

utilizado como indicador de desempeño. Además, si la función de transferencia de cable está incluida en la trayectoria de retroalimentación, el amplificador exhibe mejores respuestas transitorias amortiguadas que las que se pueden obtener de otros tipos de compensación seleccionados para producir un margen de fase equivalente. Las ventajas asociadas con la compensación de plomo reflejan principalmente el valor más alto para la frecuencia cruzada y el ancho de banda de bucle cerrado correspondientemente más alto que con frecuencia es posible con este método. Debe enfatizarse, sin embargo, que el ancho de banda superior a los requerimientos suele deteriorar el desempeño general. Un ancho de banda mayor aumenta la susceptibilidad al ruido de un amplificador y frecuentemente conduce a mayores problemas de estabilidad debido a la inductancia o capacitancia parásita.

La compensación de plomo generalmente agrava el problema de estabilidad si el bucle también incluye elementos que proporcionan un gran desplazamiento de fase negativo en un amplio rango de frecuencias sin una atenuación de magnitud correspondiente. (Si bien las limitaciones de la realizabilidad física impiden elementos que proporcionan un desplazamiento de fase positivo sin un aumento de amplitud, la conversación menos útil descrita anteriormente ocurre con una frecuencia angustiante). Por ejemplo, considere un sistema que combine una ganancia independiente de la frecuencia en un bucle con un retardo de tiempo de\(\tau\) -segundo como el proporcionado por una línea de retardo. El negativo de la transmisión en bucle para este sistema es

\[a(s) f(s) = a_0 e^{-s \tau} \nonumber \]

Figura 5.18 Prueba de Nyquist para\(a(s) f(s) = a_0 e^{-s\tau}\).

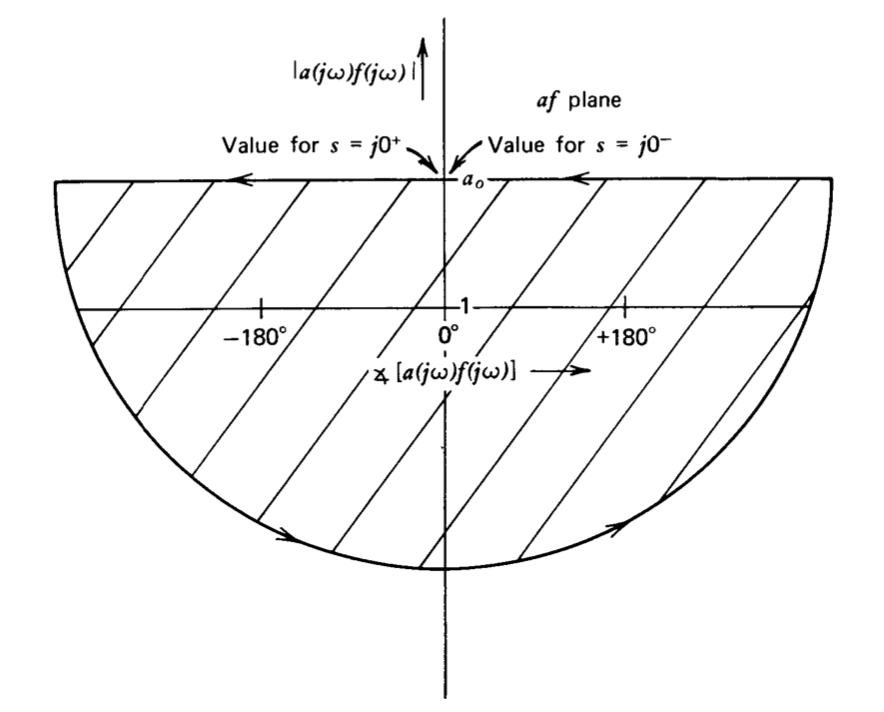
El retardo de tiempo es un elemento que tiene una magnitud de ganancia de uno en todas las frecuencias y un desplazamiento de fase negativo que está linealmente relacionado con la frecuencia. El diagrama de Nyquist (Figura 5.18) para este sistema muestra que es inestable para\(a_0 > 1\). El uso de compensación de plomo complica el problema, ya que el desplazamiento de fase positivo de la red de plomo no puede contrarrestar el desplazamiento de fase negativo ilimitado del retardo de tiempo, mientras que el aumento de magnitud de la función de plomo disminuye aún más la desensitividad máxima de baja frecuencia consistente con un funcionamiento estable.

El enfoque correcto es usar un polo dominante para disminuir la magnitud de la transmisión en bucle antes de que el cambio de fase del retardo de tiempo se vuelva excesivo. El caso limitante de un integrador (polo en el origen) funciona bien, y esta modificación da como resultado

\[a(s) f(s) = \dfrac{a_0}{s} e^{-s \tau} \nonumber \]

La insensitividad de esta función es infinita en d-c. El lector debe convencerse de que el sistema es absolutamente estable para cualquier valor positivo de\(a_0 < \pi / 2\tau\), y que al menos\(45^{\circ}\) de margen de fase se obtiene con positivo\(a_0 < \pi /4\tau\).

El uso de la compensación de retraso introduce un tipo de error que compromete su valor en algunas aplicaciones. Si la respuesta escalonada de un amplificador con retraso compensado se examina con suficiente detalle, a menudo se encuentra que incluye una larga constante de tiempo, “cola” de pequeña amplitud, que puede aumentar desordinadamente el tiempo requerido para asentarse en una pequeña fracción del valor final. De manera similar, aunque el coeficiente de error ei puede ser bastante pequeño, el tiempo requerido para que el error de rampa alcance su valor de estado estacionario puede parecer incompatible con la frecuencia de cruce del amplificador.

Como ayuda para entender este problema, considere un sistema con\(f(s) = 1\) y

\[a(s) = \dfrac{1000 (0.1 s + 1)}{s (s + 1)}\label{eq5.2.24} \]

Esta función de transferencia es una representación idealizada de un sistema que combina un solo polo dominante con compensación de lag para mejorar la desensitividad. El cero de la red de rezago se ubica a un factor de 10 por debajo de la frecuencia de cruce. La función de transferencia de bucle cerrado es

\[A(s) = \dfrac{a(s)}{1 + a(s)f(s)} = \dfrac{(0.1s + 1)}{10^{-3} s^2 + 0.101s + 1} = \dfrac{(0.1s + 1)}{(0.09s + 1)(0.011s + 1)} \nonumber \]

La respuesta de este sistema a un paso de unidad se evalúa fácilmente a través de técnicas de Laplace, con el resultado

\[v_o (t) = 1 - 1.126 e^{-t/0.011} + 0.126 e^{-t/0.09}\label{eq5.2.26} \]

Esta respuesta escalonada alcanza el 10% del valor final en 0.02 segundos, un valor razonable en vista de la frecuencia de cruce de 100 radianes por segundo del sistema. Sin embargo, el tiempo requerido para alcanzar el 1% del valor final es de 0.23 segundos debido al término final en la Ecuación\(\ref{eq5.2.26}\). Tenga en cuenta que si\(a(s)\) se cambia a\(100/s\), una función de transferencia con la misma frecuencia de ganancia de unidad que Ecuación\(\ref{eq5.2.24}\) y menor magnitud de ganancia en todas las frecuencias por debajo de 10 radianes por segundo, el tiempo requerido para que la respuesta de paso del sistema alcance el 1% del valor final es aproximadamente 0.05 segundo.

Figura 5.19 Diagrama de locus raíz para\(a(s)f(s) = a_0 (0.1s + 1)/[s(s + 1)]\).

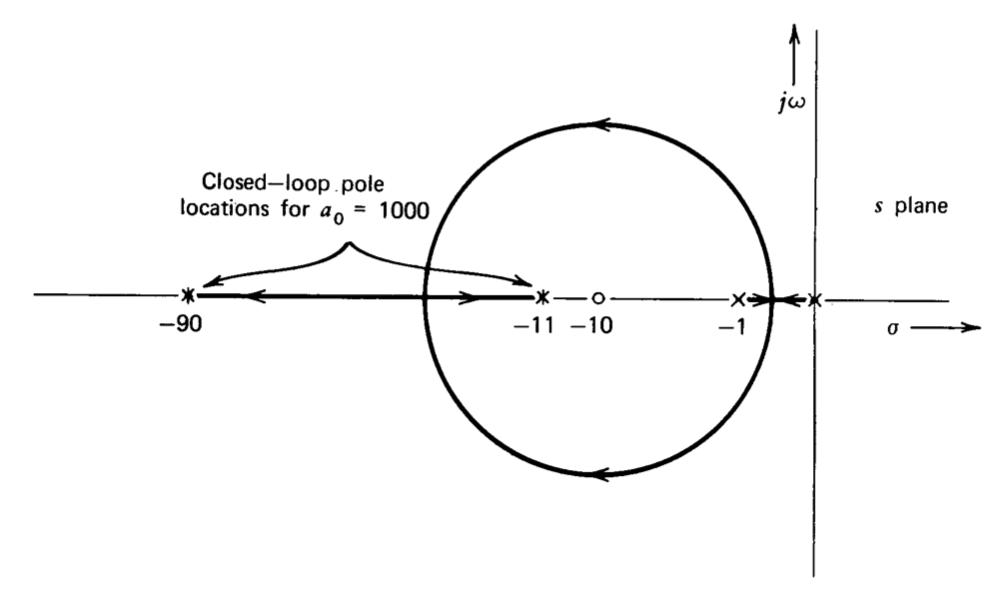
El diagrama raíz-locus para el sistema (Figura 5.19) aclara la situación. El sistema tiene un cero de bucle cerrado con una frecuencia de esquina a 10 radianes por segundo ya que el cero que se muestra en el diagrama es una singularidad de trayectoria directa. La retroalimentación obliga a un polo de bucle cerrado a acercarse a este cero. El doblete polo cero estrechamente espaciado resultante agrega una cola constante de tiempo largo a la respuesta transitoria del sistema que de otro modo se comportaría bien. El lector debe recordar que es precisamente este tipo de doblete el que deteriora la respuesta escalonada de una sonda de osciloscopio mal compensada. Dado que las relaciones lineales del sistema requieren que la respuesta de rampa sea la integral de la respuesta escalonada, el tiempo requerido para que el error de rampa alcance el valor final se retrasa de manera similar.

Cálculos similares muestran que a medida que la función de transferencia de retardo se mueve más por debajo del cruce, la amplitud de la cola disminuye, pero su constante de tiempo aumenta. Se concluye que si bien la compensación de lag es una técnica poderosa para mejorar la desensitividad, se debe utilizar con cuidado cuando se restringe el tiempo requerido para que la respuesta escalonada se asiente a una pequeña fracción de su valor final o el tiempo requerido para que el error de rampa alcance el valor final.

Se debe enfatizar que un polo de bucle cerrado generalmente se ubicará cerca de cualquier cero de bucle abierto con una frecuencia de ruptura por debajo de la frecuencia de cruce. Por lo tanto, el tipo de cola asociada con la compensación de retraso también puede resultar con, por ejemplo, una compensación de plomo que a menudo incluye un cruce por debajo de cero. La diferencia de rendimiento resulta porque el cero y el polo de bucle cerrado que se acerca a él para formar un doblete generalmente se ubican cerca de la frecuencia de cruce para la compensación de plomo. Así, el tiempo de decaimiento de la cola resultante, que está determinado por el polo de bucle cerrado en cuestión, no alarga mucho el tiempo de asentamiento del sistema.

Cuadro 5.1 Comparación de los métodos de compensación de serie

Tipo	Consideraciones especiales	Ventajas	Desventajas
Reducida\(a_0 f_0\)		Sencillez	La menor desensitividad.
Crear polo dominante	Baje la frecuencia del polo dominante existente si es posible. Localizar en la salida de un regulador.	Puede mejorar la inmunidad del aplomo del sistema. Por lo general, el tipo de elección para un regulador.	Baja el ancho de banda.
Relag	Localiza muy por debajo de la frecuencia de cruce.	Mejor desensitividad que cualquiera de los anteriores.	Puede agregar “cola” indeseable a la respuesta transitoria.
Plomo	Localice cero cerca de la frecuencia de cruce.	Mayor densensibilidad. Coeficientes de error más bajos. Respuesta transitoria más rápida.	Aumenta la sensibilidad al ruido. No se puede usar con elementos fijos que aporten un desplazamiento de fase negativo excesivo.

Es difícil desarrollar reglas generalizadas en materia de compensación, ya que el enfoque adecuado depende en gran medida de los elementos fijos incluidos en el bucle, de los tipos de entradas anticipadas, del criterio de desempeño elegido, y de muchos otros factores. A pesar de esta reserva, el Cuadro 5.1 es un intento de resumir las características más importantes de los cuatro tipos de compensación de series descritos en esta sección.