5.3: Compensación de retroalimentación
- Page ID
- 84238
La compensación en serie se logra agregando un elemento en cascada a un sistema de retroalimentación de bucle único. La compensación de retroalimentación se implementa agregando un elemento de retroalimentación que crea un sistema de dos bucles. Una posible topología se ilustra en la Figura 5.20. La función de transferencia de bucle cerrado para este sistema es
\[\dfrac{V_o}{V_i} = \dfrac{a_1 a_2/(1 + a_2 f_2)}{1 + a_1 a_2f_1/(1 + a_2 f_2)} \nonumber \]
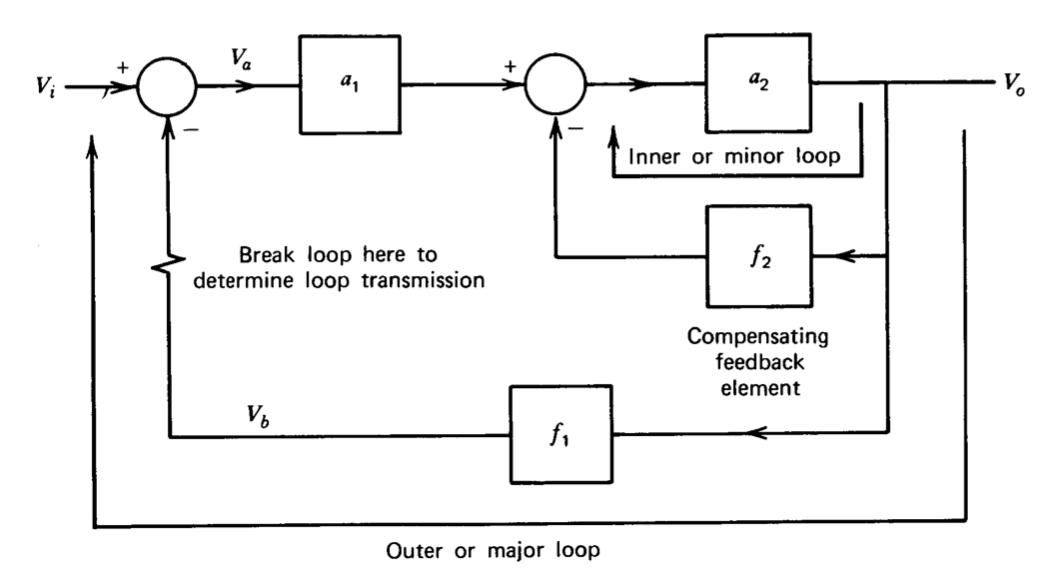
En la Figura 5.21 se muestra un sistema compensado en serie con un elemento de retroalimentación idéntico al elemento de retroalimentación de bucle principal de la Figura 5.20. Los dos elementos de retroalimentación son idénticos ya que se supone que se requiere la misma función de transferencia de bucle cerrado ideal de los dos sistemas.
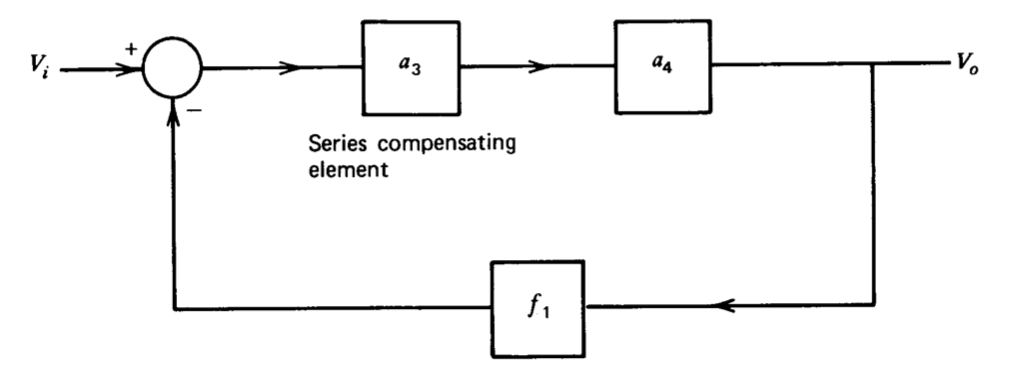
La función de transferencia de bucle cerrado para el sistema compensado en serie es
\[\dfrac{V_o}{V_i} = \dfrac{a_3 a_4}{1 + a_3 a_4 f_1} \nonumber \]
Las funciones de transferencia de bucle cerrado de los sistemas compensados por retroalimentación y serie serán iguales si\(f_2\) se selecciona de manera que
\[a_3 = \dfrac{a_1 a_2}{(1 + a_2 f_2) a_4}\label{eq5.3.3} \]
o
\[f_2 = \dfrac{a_1 a_2 - a_3 a_4}{a_2 a_3 a_4}\label{eq5.3.4} \]
El análisis anterior sugiere que una forma de seleccionar la compensación de retroalimentación adecuada es primero determinar la compensación de serie que produce un rendimiento aceptable y luego convertir a una compensación de retroalimentación equivalente. En la práctica, normalmente no se utiliza este enfoque, sino que se determina la compensación en serie para aprovechar las ventajas potenciales de este método.
Veremos que si un amplificador operacional está diseñado para aceptar compensación de retroalimentación, el uso de esta técnica a menudo da como resultado un rendimiento superior al que se puede lograr con la compensación en serie. La ventaja frecuente de la compensación de retroalimentación no es consecuencia de ningún error en las matemáticas que condujo a la equivalencia de Ecuación\(\ref{eq5.3.3}\),\(\ref{eq5.3.4}\) sino que es resultado de factores prácticos que no entran en estos cálculos. Por ejemplo, la red de compensación requerida para obtener un rendimiento de bucle cerrado especificado a menudo es más fácil de determinar e implementar y puede ser menos sensible a variaciones en otros parámetros del amplificador en el caso de un amplificador compensado por retroalimentación. De manera similar, los problemas asociados con las no linealidades y el ruido a menudo se acentúan por la compensación en serie, pero en realidad pueden reducirse por compensación de retroalimentación.
El enfoque para encontrar el tipo de compensación de retroalimentación que se debe utilizar en una aplicación dada es considerar lo negativo de la transmisión de bucle para el sistema de la Figura 5.20. Esta cantidad es
\[\dfrac{V_b}{V_a} = a_1 f_1 \dfrac{a_2}{1 + a_2 f_2} \nonumber \]
Si el bucle interno es estable (es decir, si no\(1 + a_2f_2\) tiene ceros en la mitad derecha del\(s\) plano), entonces
\[\dfrac{V_b (j \omega)}{V_a (j \omega)} \simeq \dfrac{a_1 (j \omega) f_1 (j \omega)}{f_2 (j \omega)} \ \ \ \ |a_2 (j \omega) f_2 (j \omega)| \gg 1\label{eq5.3.6} \]
y
\[\dfrac{V_b (j \omega)}{V_a (j \omega)} \simeq a_1 (j \omega) f_1 (j \omega)a_2 (j \omega) \ \ \ \ |a_2 (j \omega) f_2 (j \omega)| \ll 1\label{eq5.3.7} \]
En la práctica, los parámetros del sistema se seleccionan frecuentemente para que la magnitud de la transmisión del bucle menor sea grande en frecuencias donde la magnitud de la transmisión del bucle mayor sea cercana a una. La aproximación de la Ecuación\(\ref{eq5.3.7}\) puede entonces ser utilizada para determinar un valor para\(f_2\) que asegure la estabilidad para el sistema.
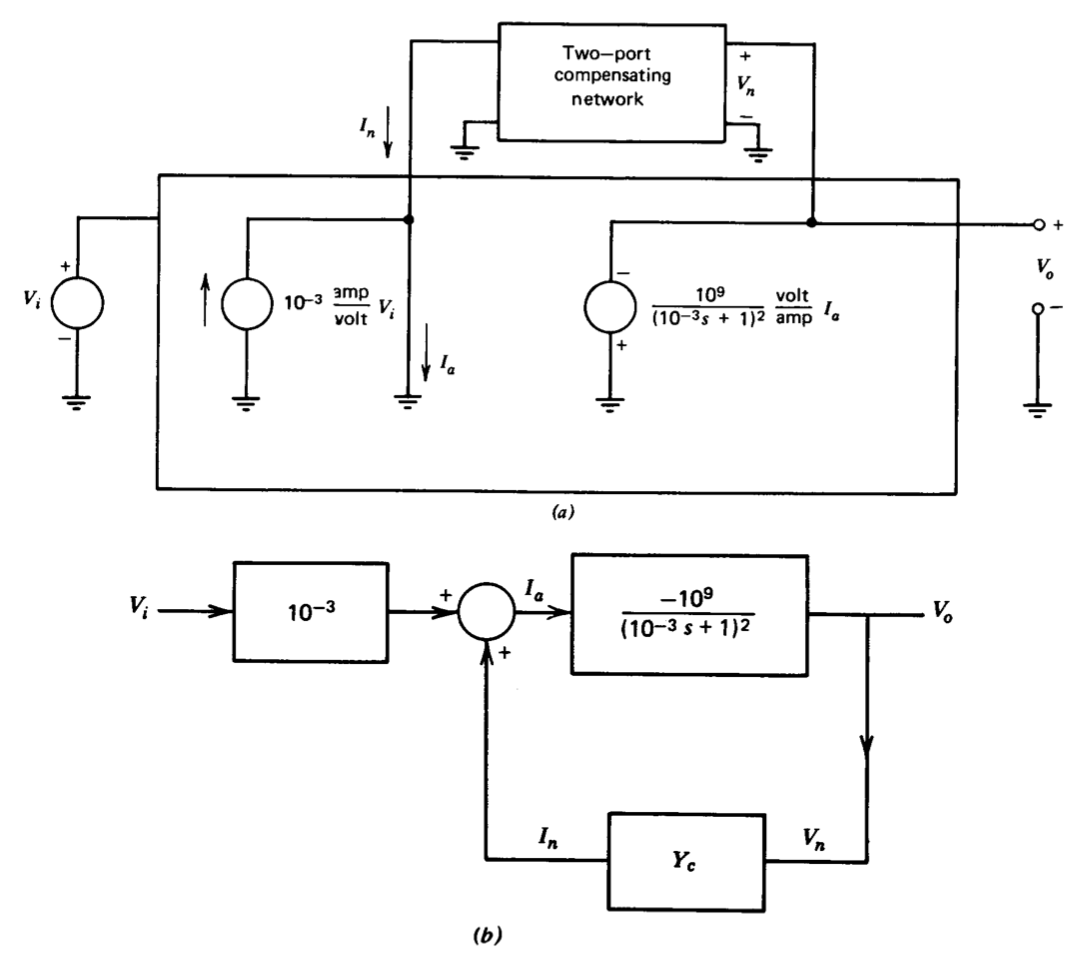
Un ejemplo simple de compensación de retroalimentación es proporcionado por el modelo de amplificador operativo que se muestra en la Figura 5.22\(a\). El modelo es una idealización de una topología de amplificador común que se investigará en detalle en secciones posteriores. El amplificador modelado incluye una primera etapa con ancho de banda amplio en comparación con el resto del circuito que conduce a una segunda etapa que tiene
impedancia de entrada relativamente baja y que domina la dinámica no compensada del amplificador. La compensación es proporcionada por una red de dos puertos que está conectada alrededor de la segunda etapa y que forma un bucle menor. Esta red está restringida a ser pasiva. En la Figura 5.22 se muestra un diagrama de bloques para el amplificador\(b\). La cantidad\(Y_c\) es la admisión de transferencia de cortocircuito de la red compensadora,\(I_n/ V_n\). (La convención utilizada para definir\(Y_c\) está en varianza con la notación normal de dos puertos, lo que cambiaría la dirección de referencia para\(I_n\). Esta forma se usa ya que resulta en menos signos menos en ecuaciones posteriores).
Si no se utiliza compensación, la función de transferencia de bucle abierto para el amplificador es
\[\dfrac{V_o (s)}{V_i (s)} = -\dfrac{10^6}{(10^{-3} s + 1)^2} \nonumber \]
Si se conecta un cable desde la salida del amplificador de nuevo a su entrada, creando un bucle principal con\(f = 1\), el margen de fase del sistema resultante es aproximadamente\(0.12^{\circ}\).
Cuando se incluye la compensación de retroalimentación, el diagrama de bloques muestra que la función de transferencia del amplificador es
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{-10^6/(10^{-3} s + 1)^2}{1 + 10^9 Y_c/(10^{-3} s + 1)^2}\label{eq5.3.9} \]
Una forma de mejorar el margen de fase de este amplificador cuando se usa en una conexión de retroalimentación es hacerlo\(V_o (s)/V_i(s)\) dominado por un solo polo. La ecuación\(\ref{eq5.3.9}\) muestra que
\[\dfrac{V_o (j\omega)}{V_i (j\omega)} \simeq \dfrac{-10^{-3}}{Y_c (j\omega)} \text{ when } \left | \dfrac{10^9 Y_c (j\omega)}{(10^{-3} j \omega + 1)^2} \right | \gg 1 \nonumber \]
Si\(C\) se utiliza un solo condensador para la red de compensación,\(Y_c = Cs\) y
\[\dfrac{Y_o (j\omega)}{Y_i (j\omega)} \simeq \dfrac{-10^{-3}}{j \omega C} \nonumber \]
para todas las frecuencias de tal manera que
\[\left |\dfrac{10^9 Cj \omega}{(10^{-3} j \omega + 1)^2} \right | \gg 1\nonumber \]
La expresión exacta para la función de transferencia de bucle abierto del amplificador con esta compensación es
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{-10^6 / (10^{-3} s + 1)^2}{1 + 10^9 Cs/ (10^{-3} s + 1)^2} = \dfrac{-10^6}{10^{-6} s^2 + (2 \times 10^{-3} + 10^9 C)s + 1} \nonumber \]
Si se utiliza un condensador de 840-pF para\(C\), la función de transferencia se convierte en
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{-10^6}{(0.84s + 1)(1.19 \times 10^{-6} s + 1)} \nonumber \]
y\(45^{\circ}\) se asegura un margen de fase de al menos para la retroalimentación independiente de la frecuencia con cualquier magnitud menor que una aplicada alrededor del amplificador. Con este valor de elemento de retroalimentación compensador,
\[-\dfrac{V_o(j \omega)}{V_i (j \omega)} \simeq \dfrac{1.19 \times 10^6}{j\omega} = \dfrac{10^{-3}}{Cj\omega} = \dfrac{10^{-3}}{Y_c (j\omega)} \nonumber \]
a cualquier frecuencia entre 1.19 radianes por segundo y\(0.84 \times 10^6\) radianes por segundo. Las dos frecuencias delimitadoras son aquellas en las que la magnitud de la transmisión de bucle compensador es una. El punto esencial es que la retroalimentación de bucle menor controla la función de transferencia del amplificador durante casi seis décadas de frecuencia. También observamos que a pesar de que se ha creado un polo dominante mediante compensación de retroalimentación, la frecuencia de ganancia unitaria del amplificador compensado (aproximadamente\(8 \times 10^5\) radianes por segundo) permanece cerca del valor no compensado de\(10^6\) radianes por segundo.
La compensación de retroalimentación es una técnica de compensación potente y de uso frecuente para los amplificadores operativos modernos. Se proporcionarán varios ejemplos de este tipo de compensación después de que se hayan descrito las topologías de circuito de amplificadores representativos.
PROBLEMAS
Ejercicio\(\PageIndex{1}\)
Un amplificador operacional tiene una función de transferencia de bucle abierto
\[a(s) = \dfrac{2 \times 10^5}{(0.1s + 1)(10^{-5} s + 1)^2}\nonumber \]
Diseñe una conexión que utilice este amplificador para proporcionar una ganancia ideal de - 10. Incluir provisión para disminuir la magnitud de la transmisión en bucle de manera que el sobreimpulso en respuesta a un paso unitario sea del 10%. Puede utilizar las curvas de la Figura 4.26 como ayuda para determinar la atenuación requerida.
Ejercicio\(\PageIndex{2}\)

Un amplificador operacional está conectado como se muestra en la Figura 5.23\(a\). El valor de\(\alpha\) se ajusta para controlar la estabilidad de la conexión. Supongamos que el ruido asociado con el amplificador puede modelarse como se muestra en la Figura 5.23\(b\). Evaluar el ruido en la salida del amplificador en función de\(\alpha\), descuidando la carga en la entrada y la salida del amplificador. Tenga en cuenta que un aumento en el ruido en la salida del amplificador implica una disminución en la relación señal/ruido, ya que la ganancia de entrada a salida es esencialmente independiente de\(\alpha\).
Ejercicio\(\PageIndex{3}\)
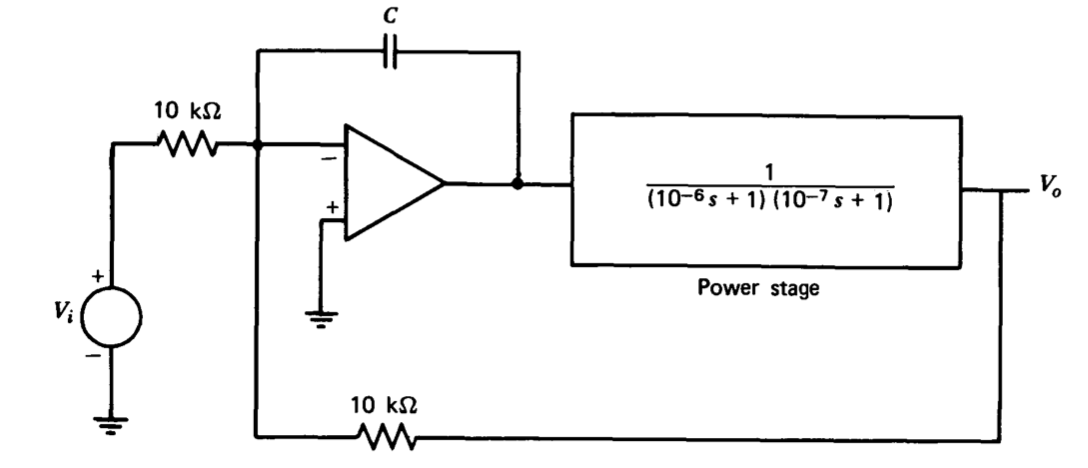
Un cierto amplificador de retroalimentación se puede modelar como se muestra en la Figura 5.24. Se puede suponer que el amplificador operacional incluido en este diagrama es ideal. Seleccione un valor para el condensador\(C\) que dé como resultado un margen de fase del sistema de\(45^{\circ}\).
Ejercicio\(\PageIndex{4}\)
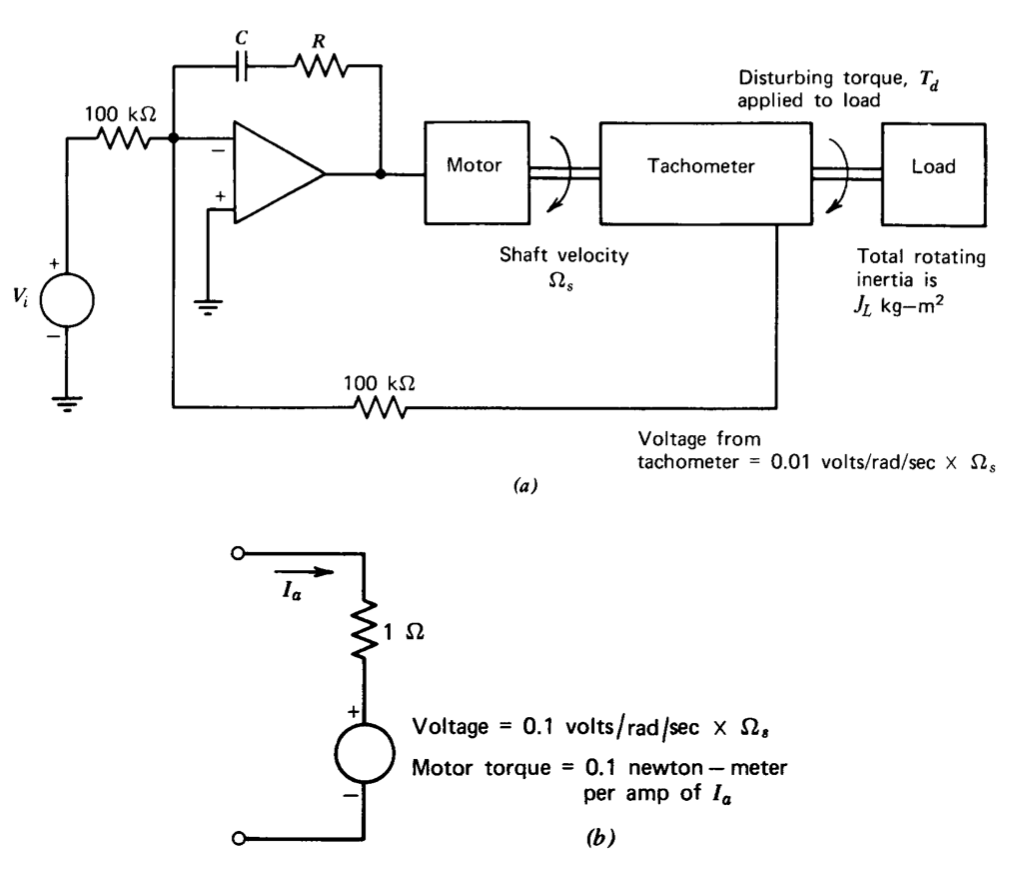
Un sistema de control de velocidad combina un amplificador operacional de alta potencia en bucle con un motor y un tacómetro como se muestra en la Figura 5.25. El tacómetro proporciona un voltaje proporcional a la velocidad del eje de salida, y este voltaje se usa como señal de retroalimentación para efectuar el control de velocidad.
- Dibuje un diagrama de bloques para este sistema que incluya los efectos del par perturbador.
- Determinar los valores de los componentes de compensación (\(R\)y\(C\)) en función de\(J_L\) para que la transmisión del bucle del sistema sea\(- 100/s\).
- Demostrar que, con este tipo de transmisión en bucle, la velocidad de salida en estado estacionario es independiente de cualquier par de carga constante.
- Utilice un análisis de coeficiente de error para mostrar que el sistema es menos sensible a pares perturbadores variables en el tiempo cuando se\(J_L\) utilizan valores mayores de. Supongamos que\(R\) y\(C\) se cambian con\(J_L\) para mantener la transmisión en bucle indicada en parte\(b\).
Ejercicio\(\PageIndex{5}\)
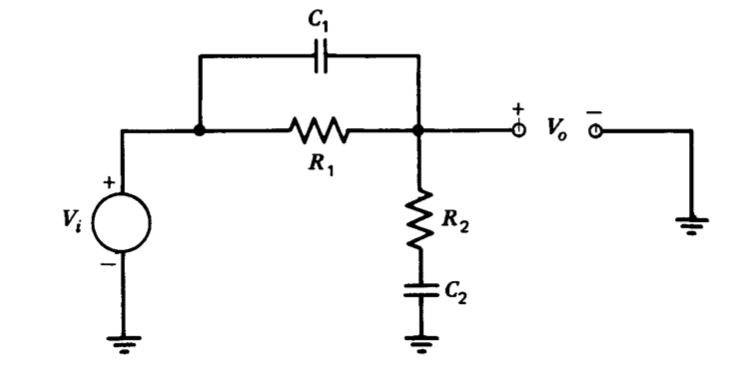
Mostrar que la red ilustrada en la Figura 5.26 puede ser utilizada para combinar una función de transferencia de retardo con una función de transferencia de plomo ubicada a una frecuencia más alta. Determinar los parámetros de red que darán como resultado la función de transferencia
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{(0.1s + 1)(10^{-2} s + 1)}{(s + 1)(10^{-3} s + 1)}\nonumber \]
Ejercicio\(\PageIndex{6}\)
La transmisión en bucle de un sistema de retroalimentación se puede aproximar como
\[L(s) = -\dfrac{10^6}{s^2} \nonumber \]
en las proximidades de la frecuencia de ganancia de unidad. Supongamos que una función de transferencia de leads (Ecuación 5.2.4) con un valor de a = 10 se puede agregar a la misión trans de bucle. ¿Cómo debe ubicarse la función de transferencia para maximizar el margen de fase? ¿Qué valores de margen de fase y frecuencia de cruce resultan?
Ejercicio\(\PageIndex{7}\)
Utilice un diagrama de bloques para mostrar que una función de transferencia de retardo se puede introducir en la transmisión en bucle del amplificador de ganancia de diez (Figura 5.9) derivando la resistencia\(R\) valorada con una red apropiada.
- Elija los parámetros de red para que la transmisión en bucle del sistema esté dada por la Ecuación 5.2.17.
- Encuentre la función de transferencia de bucle cerrado y grafique la respuesta de paso de bucle cerrado para el amplificador de ganancia de diez usando valores encontrados en parte\(a\), asumiendo que las características del amplificador operativo son ideales.
- Estime la respuesta de paso de bucle cerrado para esta conexión asumiendo que la función de transferencia de bucle abierto del amplificador es la dada por la Ecuación 5.2.12.
- Comparar el rendimiento del sistema de retardo compensado desarrollado en este problema con el mostrado en la Figura 5.13 considerando tanto la estabilidad como la función de transferencia de bucle cerrado ideal de las dos conexiones.
Ejercicio\(\PageIndex{8}\)
Se mencionó en la Sección 5.2.4 que las posibilidades alternativas de compensación para el amplificador de ganancia de diez incluyen disminuir la magnitud de la transmisión de bucle en todas las frecuencias en un factor de 6.2 y disminuir la ubicación del polo de menor frecuencia en la función de transferencia de bucle en un factor de 6.2 por seleccionar los parámetros de red retrasada apropiados.
- Determinar topologías y valores de componentes para implementar ambos esquemas de compensación.
- Dibuje diagramas de Bode de transmisión en bucle para estos dos métodos de compensación.
- Comparar la estabilidad relativa producida por estos métodos con la proporcionada por la compensación de rezago descrita en la Sección 5.2.4.
Ejercicio\(\PageIndex{9}\)
El negativo de la transmisión en bucle para el amplificador de ganancia compensada por plomo de diez descrito en la Sección 5.2.4 es
\[a(s)f(s) = \dfrac{5 \times 10^4 (10\tau s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(\tau s + 1)}\nonumber \]
donde\(\tau\) se determina por los valores de resistencia y condensador utilizados en la red de retroalimentación (ver Ecuación 5.2.15). Utilice contornos de raíz para evaluar la estabilidad del amplificador de ganancia de diez en función del parámetro\(\tau\). Encuentra el valor de\(\tau\) que maximiza la relación de amortiguación del par de polos dominante. Nota. Dado que es necesario factorizar polinomios de tercer y cuarto orden para completar este problema, se sugiere el uso de cómputos de máquina. También se sugieren cálculos numéricos para evaluar la relación de amortiguación máxima.
Ejercicio\(\PageIndex{10}\)
El negativo de la transmisión de bucle para el amplificador con retraso compensado es
\[a(s)f(s) = \dfrac{5 \times 10^4 (\tau s + 1)}{(s + 1)(10^{-4} s + 1)(10^{-5} s + 1)(\alpha \tau s + 1)}\nonumber \]
En la Sección 5.2.4 se demostró que la estabilidad razonable resulta para\(\alpha = 6.2\) y un valor de\(\tau\) que localiza la función retardada cero un factor de 10 por debajo del cruce. Utilice contornos de raíz para evaluar la estabilidad en función de la ubicación cero\((1/\tau)\) para\(\alpha = 6.2\). También se aplica a este cálculo la nota relativa a la conveniencia del cómputo de máquina mencionada en el Problema P5.9.
Ejercicio\(\PageIndex{11}\)
Determinar los tres primeros coeficientes de error para las transmisiones de cuatro bucles del amplificador de ganancia de diez descrito por las Ecuaciones 5.2.18 a 5.21. Supongamos que la compensación de plomo se obtiene en la ruta de retroalimentación (ver Sección 5.2.4) mientras que todas las demás compensaciones pueden considerarse ubicadas en la ruta de avance.
Ejercicio\(\PageIndex{12}\)
Un sistema de retroalimentación incluye un factor
\[\dfrac{(s^2/12) - (s/2) + 1}{(s^2/12) + (s/2) + 1}\nonumber \]
en su transmisión de bucle.
Suponga que tiene total libertad en la elección de la magnitud de transmisión de bucle d-c y la selección de singularidades adicionales en la transmisión de bucle. Determinar el tipo de compensación que maximizará la desensitividad de este sistema.
Ejercicio\(\PageIndex{13}\)
Calcular el tiempo de sedimentación (hasta 1% del valor final para una entrada de paso) para el amplificador de ganancia de diez con compensación de retardo (Ecuación 5.2.17). Contraste este valor con el de un sistema de primer orden con una frecuencia de cruce idéntica.
Ejercicio\(\PageIndex{14}\)
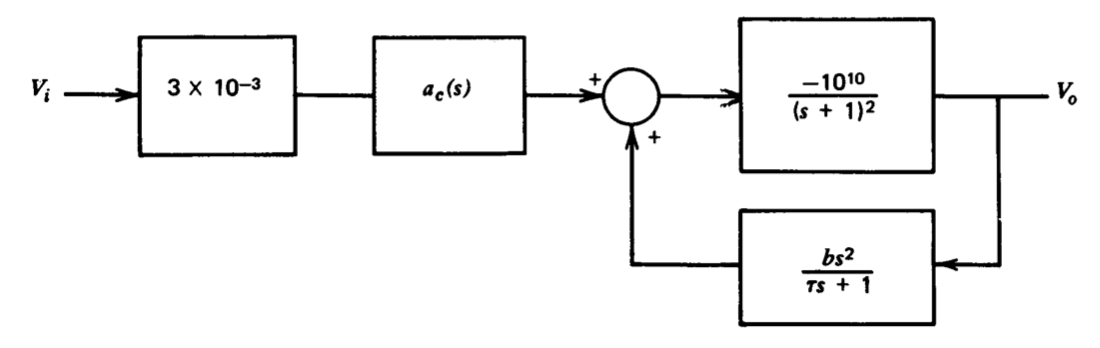
En la Figura 5.27 se muestra un modelo para un amplificador operacional que utiliza compensación de bucle menor en forma de diagrama de bloques.
a) Supongamos que el elemento compensador de serie tiene una función de transferencia\(a_c(s) = 1\). Encuentre valores para\(b\) y\(\tau\) tales que un bucle principal formado al retroalimentar\(V_o\) directamente a\(V_i\) tendrá una frecuencia de cruce de\(10^3\) radianes por segundo, aproximadamente\(55^{\circ}\) de margen de fase y máxima desensitividad a frecuencias por debajo del cruce sujeto a estos restricciones. Dibuje una gráfica Bode de bucle abierto para el amplificador con estos valores para\(b\) y\(\tau\).
b) Ahora asuma eso\(b = 0\). ¿Se puede encontrar un valor para\(a_c(s)\). que resulte en las mismas características asintóticas de magnitud de bucle abierto que obtuvo en parte\(a\), sujeto a la restricción que\(|a_c (j \omega)| \le 1\) para todos\(\omega\)?
Ejercicio\(\PageIndex{15}\)
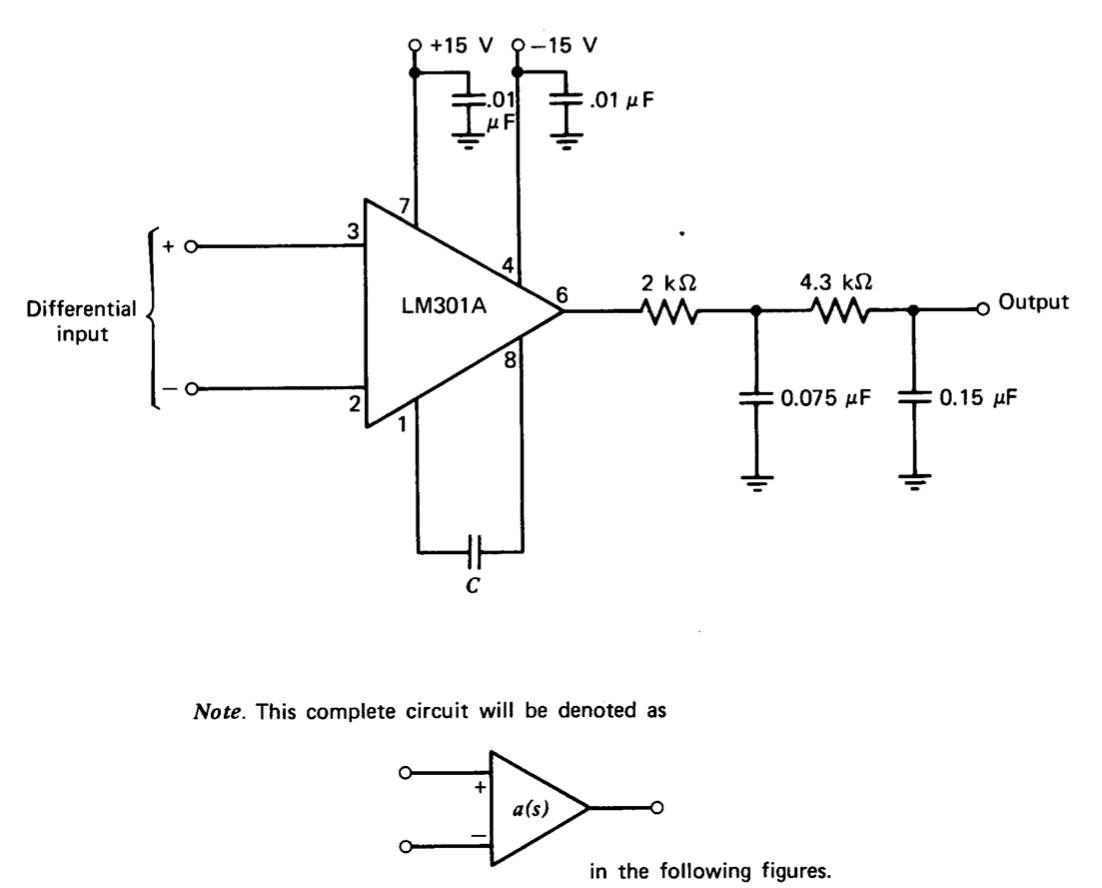
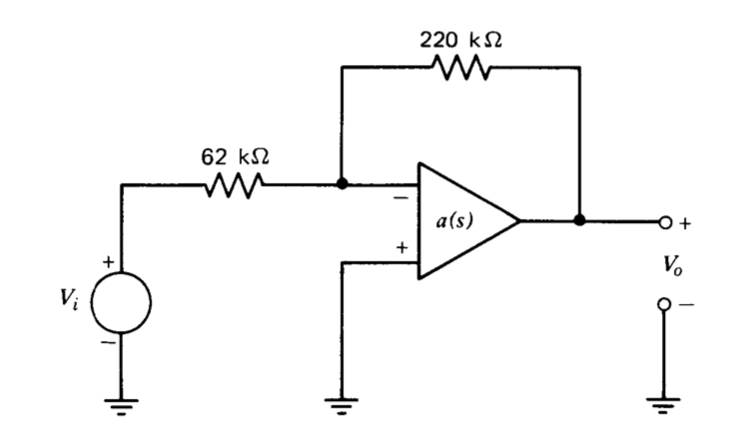
Este problema incluye una porción de laboratorio que se puede realizar con equipos de prueba comúnmente disponibles y que le dará experiencia compensando un sistema con dinámicas bien definidas. El vehículo experimental es el circuito que se muestra en la Figura 5.28, el cual da características de tipo amplificador operacional bastante repetibles. Los experimentos sugeridos utilizan la configuración a frecuencias relativamente bajas, de modo que los inevitables elementos del circuito parásito tienen poco efecto en el rendimiento medido.
Primero se debe estandarizar la dinámica del circuito. Conéctelo como amplificador inversor como se muestra en la Figura 5.29.
Seleccione el condensador\(C\) conectado entre los pines 1 y 8 del LM301A para que la configuración esté justo al borde de la inestabilidad. Un valor estimado debe estar alrededor de 5000 pF. Por favor, recuerde que el amplificador reacciona muy mal (generalmente muriendo) si los pines 1 o 5 están cortocircuitados a casi cualquier potencial.
Nota. Los supuestos requeridos para el análisis lineal se ven gravemente comprometidos si la magnitud pico a pico de la señal de entrada excede aproximadamente 50 mV. También es necesario tener la impedancia de la fuente de accionamiento baja en esta y otras conexiones. Se sugiere un divisor resistivo que atenúa la salida del generador de señal y se encuentra cerca del amplificador.
Después de esta estandarización, se afirma que si las cargas aplicadas al amplificador son mucho mayores que la impedancia de salida de la red que involucra el condensador de 0.15\(\mu\) F, etc., podemos aproximarnos\(a(s)\) como
\[a(s) \simeq \dfrac{5 \times 10^4}{(s + 1)(10^{-3}s + 1)(10^{-4} s + 1)} \nonumber \]
para fines de análisis de estabilidad. Esta función de transferencia no es única y, en general, funciones de la forma
\[a(s) = \dfrac{5 \times 10^4 \tau}{(\tau s + 1)(10^{-3} s + 1)(10^{-4} s + 1)} \nonumber \]
arrojará resultados equivalentes en su análisis proporcionando\(\tau \gg 10^{-3}\) segundos. Suministrar un argumento convincente por qué la familia de funciones de transferencia anterior representa adecuadamente el amplificador operativo que acaba de llevar al borde de la oscilación. Tenga en cuenta que simplemente mostrar las dos expresiones dadas son equivalentes no es suficiente. Debe mostrar por qué se pueden utilizar para analizar el circuito estandarizado.
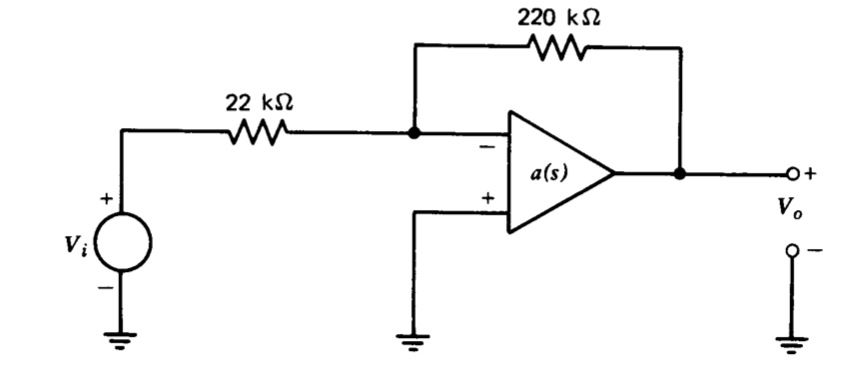
Utilice una gráfica Bode para determinar el margen de fase de la conexión que se muestra en la Figura 5.30 cuando se utiliza el amplificador estandarizado. Predecir un valor para\(M_p\) basado en el margen de fase y compara tu predicción con los resultados medidos.
Se debe compensar al sistema para mejorar su margen de fase al reducir\(a_0f_0\) y\(60^{\circ}\) mediante el uso de técnicas de compensación de lag y lead. No puede cambiar el valor\(C\) o los elementos de la red conectados a la salida del LM301A, ni cargar la red de manera injustificada para implementar la compensación.
Determine analíticamente los valores de topología y elementos que utilizará para cada una de las tres formas de compensación. Puede que no sea posible cumplir con el objetivo de margen de fase utilizando solo la compensación de clientes potenciales; si encuentra que este es el caso, puede reducir\(a_0f_0\) ligeramente para que se pueda lograr el objetivo de diseño.
Compensar el amplificador en el laboratorio y convencerse de que las respuestas de paso que mida son razonables para sistemas con margen\(60^{\circ}\) de fase. También correlaciona los tiempos de subida de las respuestas con tus valores predichos para frecuencias cruzadas.


