11.5: Ejemplo de Inductor de Capacitor
- Page ID
- 81887
Las ideas de cálculo de variaciones se aplican también a los procesos de conversión de energía en sistemas eléctricos. Considere un circuito con un condensador y un inductor como se muestra en la Figura\(\PageIndex{1}\). La corriente\(i_L\), la corriente\(i_c\) y el voltaje\(v\) se definen en la figura. Supongamos que los cables y componentes no tienen resistencia. Si bien esto no es completamente físico, nos permitirá simplificar el problema. Supongamos que el condensador está cargado y que el interruptor está abierto.\(t < 0\) At\(t = 0\), el interruptor está cerrado y el condensador comienza a descargar. En este ejemplo, la trayectoria generalizada será la carga acumulada en las placas del condensador. Podemos derivar la ecuación de movimiento que describe este camino.
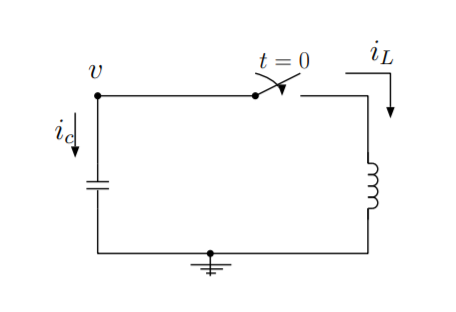
La energía se convierte entre dos formas. La primera forma de energía en este sistema es la energía eléctrica almacenada en el condensador. El voltaje\(v\) en voltios a través de un condensador es proporcional a la carga\(Q\) en culombios a través de las placas del condensador. La capacitancia\(C\), medida en faradios, es la constante de proporcionalidad entre las dos medidas.
\[Q = Cv \nonumber \]
La relación corriente-voltaje a través del condensador se puede encontrar tomando la derivada con respecto al tiempo.
\[\frac{dQ}{dt} = C\frac{dv}{dt} \label{11.5.2} \]
El cambio en la acumulación de carga con respecto al tiempo es el actual. Más específicamente,
\[\frac{dQ}{dt} = i_c = -i_L. \label{11.5.3} \]
Las ecuaciones\ ref {11.5.2} y\ ref {11.5.3} se pueden combinar.
\[-i_L = C\frac{dv}{dt}. \nonumber \]
La energía almacenada en un condensador es
\[E_{c a p}=\frac{1}{2} C v^{2}. \nonumber \]
La segunda forma de energía en este sistema es la energía almacenada en el campo magnético del inductor. La corriente\(i_L\) a través del inductor, medida en amperios, es proporcional al flujo magnético\(\Psi\), medido en webers, alrededor del inductor. La inductancia\(L\), medida en henries, es la constante de proporcionalidad entre la corriente y el flujo magnético.
\[\Psi = Li_L \nonumber \]
La relación de voltaje de corriente a través de este inductor se puede encontrar tomando la derivada con respecto al tiempo.
\[\frac{d \Psi}{d t}=v=L \frac{d i_{L}}{d t} \nonumber \]
La energía almacenada en el inductor viene dada por
\[E_{ind}=\frac{1}{2} L i_{L}^{2} \nonumber \]
Describimos el proceso de conversión de energía realizando un seguimiento de una ruta generalizada\(Q(t)\), la carga almacenada en el condensador. La variable\(t\) representa la variable independiente tiempo en segundos, y\(Q\) es la carga variable dependiente en culombios. El hamiltoniano y lagrangiano\(L\),\(H\) y, se considerarán funciones de tres variables independientes:\(t\),\(Q\), y\(\frac{dQ}{dt}\).
El hamiltoniano es la suma de la energía en el condensador y la energía en el inductor. El lagrangiano es la diferencia entre estas energías.
\[H = E_{total} = E_{cap} + E_{ind} \nonumber \]
\[\mathcal{L} = E_{cap} - E_{ind} \nonumber \]
Los ingenieros eléctricos suelen describir los circuitos físicos utilizando las cantidades más fáciles de medir: corriente y voltaje. Sin embargo, aquí para ilustrar el uso del formalismo de cálculo de variaciones, escribimos expresiones tanto para la energía total como para la lagrangiana en términos de las variables especificadas:\(t\),\(Q\), y\(\frac{dQ}{dt}\).
\[H\left(t, Q, \frac{d Q}{d t}\right)=\frac{1}{2 C} Q^{2}+\frac{1}{2} L\left(\frac{d Q}{d t}\right)^{2} \nonumber \]
\[\mathcal{L}\left(t, Q, \frac{d Q}{d t}\right)=\frac{1}{2 C} Q^{2}-\frac{1}{2} L\left(\frac{d Q}{d t}\right)^{2} \nonumber \]
Podemos encontrar el camino, cargar en el condensador en función del tiempo, resolviendo para la menor acción
\[\delta\left|\int_{t_{1}}^{t_{2}} \mathcal{L}\left(t, x, \frac{d x}{d t}\right) d t\right|=0 \label{11.5.13} \]
o resolviendo la ecuación de Euler-Lagrange,
\[\frac{\partial \mathcal{L}}{\partial Q}-\frac{d}{d t} \frac{\partial \mathcal{L}}{\partial\left(\frac{d Q}{d t}\right)}=0. \label{11.5.14} \]
En la Ecuación\ ref {11.5.13},\(\delta\) indica la primera variación definida por la Ecuación 11.3.5. Las soluciones dependen de condiciones iniciales como la carga almacenada en el condensador y la corriente en el inductor en el momento inicial. Podemos usar la ecuación de Euler-Lagrange para encontrar la ecuación del movimiento. El primer término de la Ecuación\ ref {11.5.14} es el potencial generalizado,
\[\frac{\partial \mathcal{L}}{\partial Q} = \frac{Q}{C} \nonumber \]
que es el voltaje\(v\) en voltios. El siguiente término es el derivado del impulso generalizado.
\[\mathbb{M}=\frac{\partial \mathcal{L}}{\partial\left(\frac{d Q}{d t}\right)}=-L \frac{d Q}{d t} \nonumber \]
Podemos juntar las piezas para encontrar una expresión de conservación del potencial generalizado.
\[\frac{Q}{C}+L \frac{d^{2} Q}{d t^{2}}=0 \label{11.5.17} \]
Esta es una declaración de la ley de tensión de Kirchhoff. Parece más familiar si está escrito en términos de voltaje\(v = \frac{Q}{C}\) y corriente\(i_L = -\frac{dQ}{dt}\).
\[v-L \frac{d i_{L}}{d t}=0 \nonumber \]
Podemos resolver la ecuación de movimiento, Ecuación\ ref {11.5.17}, usando las condiciones iniciales apropiadas, para encontrar el camino. Como en el ejemplo del resorte de masa, la Ecuación\ ref {11.5.17} es la ecuación de onda, y sus soluciones son sinusoides. Como era de esperar, un circuito hecho de solo un condensador y un inductor es un oscilador.
| Dispositivo de almacenamiento de energía | Capacitor | Muelle lineal |
|---|---|---|
| Ruta Generalizada | Carga\(Q\) en C | Desplazamiento\(\overrightarrow{x}\) en m |
| Potencial Generalizado | Voltaje\(v\) en\(\frac{J}{C} = V\) | \(\overrightarrow{F}\)Fuerza en\(\frac{J}{m} = N\) |
| Capacidad Generalizada | Capacitancia\(C\) en F =\(\frac{C^2}{J}\) | \(\frac{1}{K}\)en\(\frac{m^2}{J}\) |
| Relación constitutiva | \(Q=Cv\) | \(\overrightarrow{x} = \frac{1}{K}\overrightarrow{F}\) |
| Energía | \(\frac{1}{2}Cv^2\) | \(\frac{1}{2}\frac{1}{K}|\overrightarrow{x}|^2 = \frac{1}{2}K|\overrightarrow{F}|^2\) |
| Ley para el potencial | KVL | Segunda Ley de Newton\(\overrightarrow{F} = m\overrightarrow{a}\) |
Además, podemos demostrar que la energía se conserva en este proceso de conversión de energía porque la derivada parcial tanto de la energía total como de la lagrangiana con respecto al tiempo son cero.
\[\frac{\partial \mathcal{L}}{\partial t}=\frac{\partial H}{\partial t}=0 \nonumber \]
\[\frac{d \mathcal{L}}{d t}=\frac{d H}{d t}=0 \nonumber \]
Tabla\(\PageIndex{2}\) resume este ejemplo. También ilustra la relación entre los parámetros de este ejemplo y los parámetros del ejemplo de resorte de masa.


