3.2.3: Coeficientes aerodinámicos adimensionales

Las curvas fundamentales de un perfil aerodinámico son: curva de elevación, curva de arrastre y curva de momento. Estas curvas representan ciertos coeficientes adimensionales relacionados con la elevación, el arrastre y el impulso.

El interés se centra primero en determinar la distribución de presión sobre los intrados y extrados del perfil aerodinámico para que, integrando tales distribuciones, se puedan calcular las cargas globales. Nuevamente, en lugar de utilizar la distribución de presiones\(p(x)\), se\(c_p(x)\) utilizará la distribución del coeficiente de presiones.

El coeficiente de presiones se define como la presión en el punto considerado menos la presión de referencia, típicamente la presión estática de la corriente entrante\(p_{\infty}\), sobre

presión dinámica de la corriente entrante\(q = \rho_{\infty} u_{\infty}^2 /2\), es decir:

\[c_p = \dfrac{p - p_{\infty}}{\tfrac{1}{2} \rho_{\infty} u_{\infty}^2}.\]

Usando la Ecuación (3.1.3.5) y considerando densidad constante, produce:

\[c_p = 1 - \left ( \dfrac{V}{u_{\infty}} \right )^2,\]

siendo\(V\) la velocidad del flujo de aire en el punto considerado.

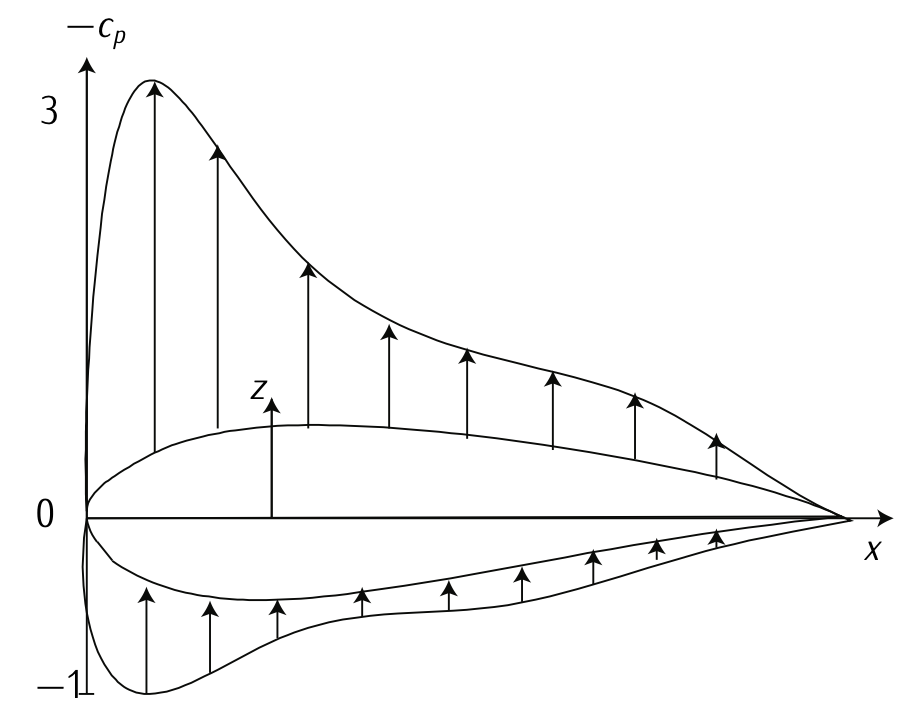
Figura 3.16. Distribución del Coeficiente de Presiones. Adaptado de\(F_{\text{RANCHINI}}\) et al. [4]

La Figura 3.16 muestra una distribución típica del coeficiente de presiones sobre un perfil aerodinámico. Observe que el eje z muestra negativo\(c_p\) y la dirección de las flechas significa el signo de\(c_p\). Una flecha que sale del perfil aerodinámico implica\(c_p\) es negativa, lo que significa que la corriente de aire se acelera en esa área (extrados del perfil aerodinámico) y la presión disminuye (succión). Por otro lado, donde las flechas ingresan al perfil aerodinámico existe sobrepresión, es decir, corriente desacelerada y positiva\(c_p\). Observe que si existe un punto de estancamiento (\(V = 0\)), que por cierto es típico,\(c_p = 1\).

Los coeficientes adimensionales son:

\[c_l = \dfrac{l}{\tfrac{1}{2} \rho_{\infty} u_{\infty}^2 c};\]

\[c_d = \dfrac{d}{\tfrac{1}{2} \rho_{\infty} u_{\infty}^2 c};\]

\[c_m = \dfrac{m}{\tfrac{1}{2} \rho_{\infty} u_{\infty}^2 c^2};\]

El criterio de los signos es el siguiente: para\(c_l\), positivo si el levantamiento va hacia arriba; para\(c_d\), positivo si el arrastre va hacia atrás; para\(c_m\), positivo si el momento hace que el avión se acueste hacia arriba.

Las ecuaciones que permiten\(c_l\) y se obtienen\(c_m\) a partir de las distribuciones de coeficientes de presión en los extrados\(c_{pe} (x)\), y los intrados\(c_{pe} (x)\), son:

\[c_l = \dfrac{1}{c} \int_{x_{le}}^{x_{te}} (c_{pi} (x) - c_{pe} (x)) dx = \dfrac{1}{c} \int_{x_{le}}^{x_{te}} c_l (x) dx,\]

\[\begin{array} {rcl} {c_m} & = & {\dfrac{1}{c^2} \int_{x_{le}}^{x_{te}} (x_0 - x) (c_{pi} (x) - c_{pe} (x)) dx = \ ...} \\ {...} & = & {\dfrac{1}{c^2} \int_{x_{le}}^{x_{te}} (x_0 - x) c_l (x) dx.} \end{array}\]

Si\(x_0\) se elige para que el momento sea nulo,\(x_0\) coincidirá con el centro de presiones del plano aerodinámico (también denominado centro aerodinámico)\(x_{cp}\), que es el punto de aplicación de la elevación vectorial:

\[x_{cp} = \dfrac{\int_{x_{le}}^{x_{te}} x c_l (x) dx}{\int_{x_{le}}^{x_{te}} c_l (x) dx}.\]

Observe que en el caso de un ala o una aeronave completa, las fuerzas de sustentación y arrastre tienen unidades de fuerza [N], y el par de cabeceo tiene unidades de impulso [Nm]. Para representarlos es de común acuerdo utilizar\(L, D\), y\(M\). En el caso de las superficies aerodinámicas, debido a su carácter bidimensional, típicamente se habla de fuerza e impulso por unidad de distancia. Para notar la diferencia, se representan como\(l, d\), y\(m\).

Curvas características

Las curvas características de un perfil aerodinámico se expresan en función de los coeficientes adimensionales. Estas curvas características son, dado un número Mach, un número de Reynolds y la geometría del perfil aerodinámico, como sigue:

• La curva de elevación dada por\(c_l (\alpha)\).
• La curva de arrastre\(c_d (c_l)\), también conocida como curva polar.
• La curva de impulso,\(c_m (\alpha)\).

Además, hay otra curva típica que representa la eficiencia aerodinámica en función de\(c_l\) dada\(\text{Re}\) y\(M\). La eficiencia aerodinámica es\(E = \tfrac{c_l}{c_d} (E = \tfrac{L}{D})\), y mide la relación entre la elevación generada y la resistencia generada. El diseñador tiene como objetivo maximizar esta relación.

Permite enfocarnos en la curva de elevación. Normalmente esta curva presenta una zona lineal, que puede aproximarse por:

\[c_l (\alpha) = c_{l0} + c_{l\alpha} \alpha = c_{l \alpha} (\alpha - \alpha_0),\]

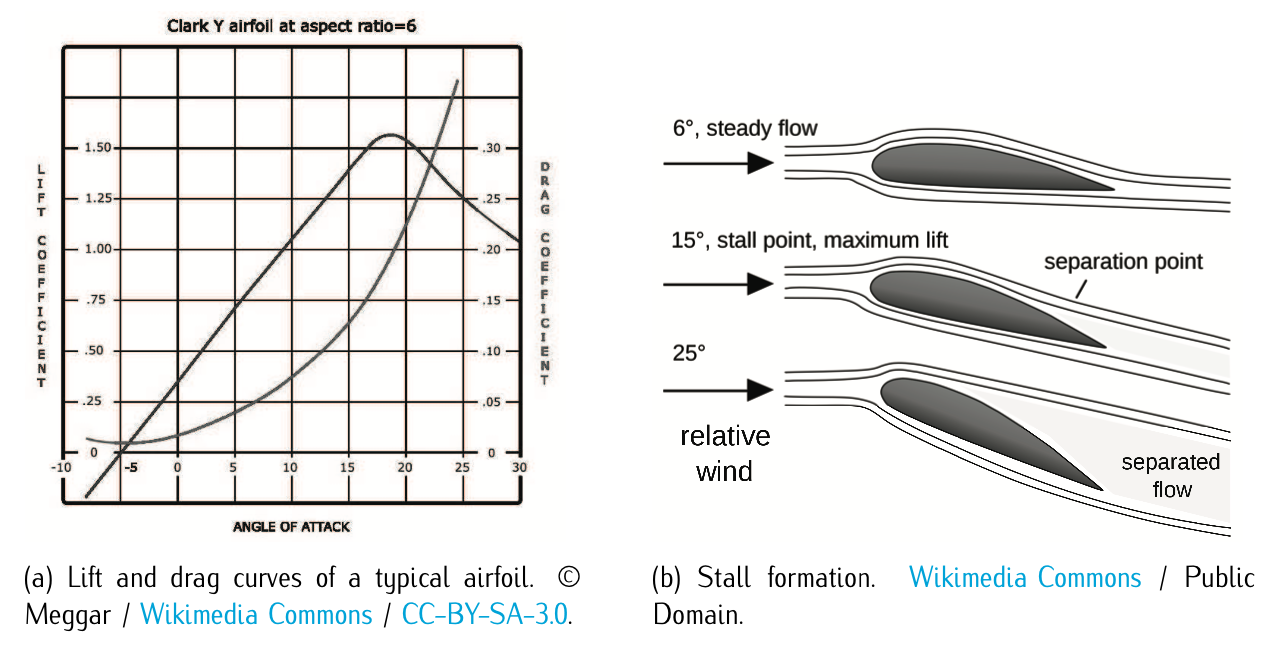
Figura 3.17: Curvas características de elevación y arrastre.

donde\(c_{l \alpha} = d c_l /d \alpha\) está la pendiente de la curva de elevación,\(c_{l0}\) es el valor de\(c_l\) for\(\alpha = 0\) y\(\alpha_0\) es el valor de\(\alpha\) for\(c_l = 0\). La teoría lineal de las superficies aerodinámicas delgadas en régimen incompresible da un valor a\(c_{l \alpha} = 2\pi\), mientras que\(c_{l0}\), que depende de la curvatura del perfil aerodinámico, es nula para los planos simétricos. Hay un ángulo de ataque, denominado ángulo de parada, en el que este comportamiento lineal ya no se mantiene. En este punto la curva presenta un máximo. Uno de este punto es que el levantamiento pasado disminuye dramáticamente. Este efecto se debe a la caída de la capa límite de la superficie aerodinámica cuando aumentamos demasiado el ángulo de ataque, reduciendo drásticamente la elevación y aumentando la resistencia debido a los efectos de presión. La Figura 3.17.b lo ilustra.

El arrastre polar puede aproximarse (bajo la misma hipótesis de flujo incompresible) a una curva parabólica de la forma:

\[c_d (c_l) = c_{d_0} + c_{d_i} c_l^2,\]

donde\(c_{d_0}\) está el coeficiente de arrastre del parásito (el que existe cuando\(c_l = 0\)) y\(c_{d_i}\) es el coeficiente inducido (arrastre inducido por elevación). Esta curva se conoce como arrastre parabólico polar.

La curva de momento puede ser aproximadamente constante (bajo la misma hipótesis de flujo incompresible) si se toma adecuadamente el punto\(x_0\). Este punto es el centro aerodinámico del perfil aerodinámico. Bajo régimen incompresible, este punto está cerca\(0.25c\).

Las curvas de elevación y arrastre se ilustran en la Figura 3.17.a para un perfil aerodinámico típico.