7.3: Problemas

Ejercicio\(\PageIndex{1}\) Performances

Considera el Airbus A-320 con las siguientes características:

• \(m = 64\ tonnes.\)
• \(S_w = 122.6\ m^2.\)
• \(C_D = 0.024 + 0.0375 C_L^2\).

1. El avión inicia una maniobra de ascenso con velocidad uniforme a 10.000 pies de altitud (3048 metros). A ese nivel de vuelo, los rendimientos típicos de la aeronave indican una velocidad con respecto al aire de 289 nudos (\(148.67\ m/s\)) y una tasa de ascenso (velocidad vertical) de\(2760\ feet/min\) (\(14\ m/s\)). Suponiendo que\(\gamma \ll 1\), calcular:
   (a) El ángulo de ascenso,\(\gamma\).
   b) Empuje requerido en esas condiciones.
2. El avión alcanza una altitud de\(11000\ m\), y realiza un vuelo horizontal, constante, recto. Determinar:
   (a) La velocidad correspondiente a la máxima eficiencia aerodinámica.
3. El piloto apaga los motores y comienza a deslizarse a una altitud de\(11000\ m\). Calcular:
   (a) La velocidad mínima de descenso (velocidad vertical), y el ángulo de descenso correspondiente,\(\gamma_d\):

Contestar

Además de los datos dados en el enunciado, se han utilizado los siguientes datos:

• \(g = 9.81\ m/s^2\).
• \(R = 287\ J/(kgK)\).
• \(\alpha_T = 6.5 \cdot 10^{-3}\ K/m\).
• \(\rho_0 = 1.225\ kg/m^3\).
• \(T_0 = 288.15\ K\).
• \(ISA: \rho = \rho_0 (1 - \tfrac{\alpha_T h}{T_0})^{\tfrac{gR}{\alpha_T} - 1}\).

1. Ascenso uniforme bajo las siguientes condiciones de vuelo:
   \(\bullet\)\(h = 3048\ m\). Usando\(ISA \to \rho = 0.904\ kg/m^3\).
   \(\bullet\)\(V = 148.67\ m/s\).
   \(\bullet\)\(h_e = 14\ m/s\).
   El sistema que rige el movimiento de la aeronave es:
   \[T = D + mg \sin \gamma;\]
   \[L = mg \cos \gamma;\]
   \[\dot{x}_e = V\cos \gamma;\]
   \[\dot{h}_e = V \sin \gamma.\]
   Suponiendo que\(\gamma \ll 1\), y así eso\(\cos \gamma \sim 1\) y \(\sin \gamma \sim \gamma\), Sistema (B.1) se convierte en:
   \[T = D + mg \gamma;\label{eq7.3.5}\]
   \[L = mg;\label{eq7.3.6}\]
   \[\dot{x}_e = V;\]
   \[\dot{h}_e = V_{\gamma}.\label{eq7.3.8}\]
   (a) De la Ecuación (\(\ref{eq7.3.8}\)),\(\gamma = \tfrac{\dot{h}_e}{V} = 0.094\ rad\ (5.39^{\circ})\).
   (b) De la Ecuación (\(\ref{eq7.3.5}\)),\(T = D + mg\gamma\).
   \[D = C_D \dfrac{1}{2} \rho S_w V^2,\label{eq7.3.9}\]
   donde\(C_D = 0.024 + 0.0375 C_L^2\), y\(\rho, S_w, V^2\) se conocen.
   \[C_L = \dfrac{L}{\tfrac{1}{2} \rho S_w V^2} = 0.512,\label{eq7.3.10}\]
   donde, de acuerdo con la Ecuación (\(\ref{eq7.3.6}\)),\(L = mg\). Con la Ecuación (\(\ref{eq7.3.10}\)) en la Ecuación (\(\ref{eq7.3.8}\)),\(D = 41398\ N\).
   Por último:
   \[T = D + mg\gamma = 100\ kN.\nonumber\]
2. Vuelo horizontal, constante, recto bajo las siguientes condiciones de vuelo:
   \(\bullet\)\(h = 11000\ m\). Usando\(ISA \to \rho = 0.3636\ kg/m^3\).
   \(\bullet\)La eficiencia aerodinámica es máxima.
   El sistema que rige el movimiento de la aeronave es:
   \[T = D;\]
   \[L = mg \cos \gamma.\label{eq7.3.12}\]
   La máxima Eficiencia es\(E_{\max} = \tfrac{1}{2\sqrt{C_{D_0} C_{D_i}}} = 16.66\).
   El coeficiente óptimo de elevación es\(C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}} = 0.8\).
   \[C_L = \dfrac{L}{\tfrac{1}{2} \rho S_w V^2} \to V = \dfrac{L}{\tfrac{1}{2} \rho S_w C_L} = 187\ m/s,\nonumber\]
   donde, de acuerdo con la Ecuación (\(\ref{eq7.3.12}\))\(L = mg\), y con el fin de volar con la máxima eficiencia:\(C_L = C_{L_{opt}}\).
3. Deslizamiento bajo las siguientes condiciones de vuelo:
   \(\bullet\)\(h = 11000\ m\). Usando\(ISA \to \rho = 0.3636\ kg/m^3\).
   \(\bullet\)A la velocidad mínima de descenso.
   El sistema que rige el movimiento de la aeronave es:
   \[D = mg\sin \gamma_d;\label{eq7.3.13}\]
   \[L = mg \cos \gamma_d;\label{eq7.3.14}\]
   \[\dot{x}_e = V \cos \gamma_d;\label{eq7.3.15}\]
   \[\dot{h}_{e_{des}} = V \sin \gamma_d.\label{eq7.3.16}\]
   Observe eso\(\gamma_d = -\gamma\).
   Suponiendo que\(\gamma_d \ll 1\), y así eso\(\cos \gamma_d \sim 1\) y\(\sin \gamma_d \sim \gamma_d\), Sistema (\(\ref{eq7.3.13}\),,\(\ref{eq7.3.14}\)\(\ref{eq7.3.15}\),\(\ref{eq7.3.16}\)) se convierte en:
   \[D = mg \gamma_d;\label{eq7.3.17}\]
   \[L = mg;\label{eq7.3.18}\]
   \[\dot{x}_e = V;\]
   \[\dot{h}_{e_{des}} = V\gamma_d.\]
   Para poder volar con la máxima velocidad de descenso\(\dot{h}_{e_{des}}\) debe ser máxima. Operando con Ecuación (\(\ref{eq7.3.17}\)) y Ecuación (\(\ref{eq7.3.18}\)),\(\gamma_d = \tfrac{D}{L}\).
   \[\dot{h}_{e_{des}} = V\gamma = V \dfrac{D}{L} = V \dfrac{(0.024 + 0.0375 C_L^2) \tfrac{1}{2} \rho S_w V^2}{C_L \tfrac{1}{2} \rho S_w V^2}.\label{eq7.3.21}\]
   sabiendo que\(C_L = \tfrac{L}{\tfrac{1}{2} \rho S_w V^2}\), donde, según la Ecuación (\(\ref{eq7.3.18}\)),\(L = mg\), Ecuación (\(\ref{eq7.3.21}\)) se convierte en:
   \[\dot{h}_{e_{des}} = \dfrac{V}{mg} \left (0.024 \dfrac{1}{2} \rho S_w V^2 + \dfrac{0.0375 (mg)^2}{\tfrac{1}{2} \rho S_w V^2} \right ).\label{eq7.3.22}\]
   make\(\tfrac{\partial \dot{h}_{e_{des}}}{\partial V} = 0\).
   La velocidad con respecto al aire para que la velocidad vertical sea mínima es:
   \[V = \sqrt[4]{\dfrac{4}{3} \dfrac{C_{D_i}}{C_{D_0}}} \sqrt{\dfrac{mg}{\rho S_w}} = 142.57\ m/s.\]
   Sustituyendo\(V = 142.57\ m/s\) en la Ecuación (\(\ref{eq7.3.22}\)),\(\dot{h}_{e_{des}} = 9.87\ m/s\).

Ejercicio\(\PageIndex{2}\) Runway performances

Queremos estimar la distancia de despegue de un Airbus A-320 despegando en el aeropuerto de Madrid-Barajas. Dicho avión monta dos turborreactores, cuyo empuje puede estimarse como:\(T = T_0 (1 - k\cdot V^2)\), donde\(T\) está el empuje,\(T_0\) es el empuje nominal,\(k\) es una constante y\(V\) es la verdadera velocidad del aire.

Considerando que:

• \(g \cdot (\tfrac{T_0}{m\cdot g} - \mu_r) = 1.31725 \tfrac{m}{s^2};\)
• \(\tfrac{\rho S(C_D - \mu_r C_L) + 2 \cdot T_0 \cdot k}{2 \cdot m} = 3.69 \cdot 19^{-5} \tfrac{m}{s^2};\)
• La velocidad de despegue es\(V_{TO} = 70\ m/s;\)

donde\(g\) esta la fuerza debida a la gravedad,\(m\) es la masa de la aeronave,\(\mu_r\) es el coeficiente de fricción,\(\rho\) es la densidad del aire,\(S\) es la superficie mojada de la aeronave,\(C_D\) es el coeficiente de sustentación ⁹.

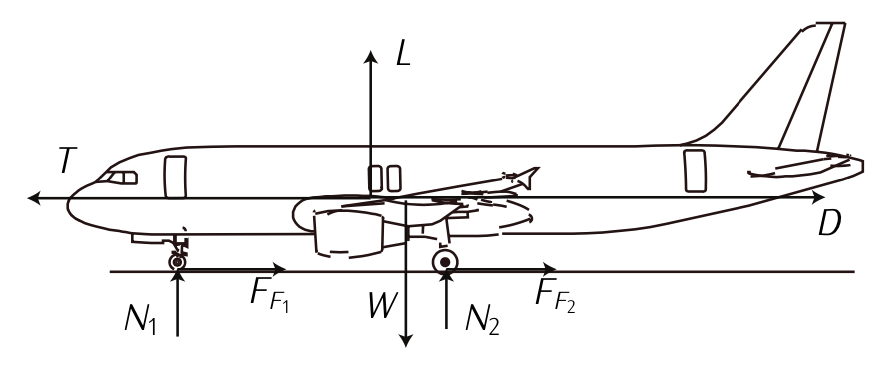
Figura 7.16: Fuerzas durante el despegue

Calcular:

1. Distancia de despegue.

Contestar

Aplicamos la 2da Ley de Newton:

\[\sum F_z = 0;\label{eq7.3.24}\]

\[\sum F_x = m \dot{V}.\label{eq7.3.25}\]

En cuanto a la Ecuación (\(\ref{eq7.3.24}\)), observe que al rodar sobre el suelo, se supone que la aeronave está en equilibrio a lo largo del eje vertical.

Mirando la Figura 7.16, la ecuación (\(\ref{eq7.3.24}\)) - (\(\ref{eq7.3.25}\)) se convierte en:

\[L + N - mg = 0;\label{eq7.3.26}\]

\[T - D - F_F = m \dot{V}.\]

siendo\(L\) la elevación,\(N\) la fuerza normal,\(mg\) el peso;\(T\) la confianza,\(D\) el arrastre y\(F_F\) la fuerza total de fricción.

Es bien sabido que:

\[L = C_L \dfrac{1}{2} \rho S V^2;\label{eq7.3.28}\]

\[D = C_D \dfrac{1}{2} \rho S V^2.\label{eq7.3.29}\]

También es bien sabido que:

\[F_F = \mu_r N.\]

La ecuación (\(\ref{eq7.3.26}\)) establece que:\(N = mg - L\). Por lo tanto:

\[F_F = \mu_r (mg - L).\label{eq7.3.31}\]

Dado que\(T = T_0 (1 - kV^2)\), con la Ecuación (\(\ref{eq7.3.31}\)) y las Ecuaciones (\(\ref{eq7.3.28}\)) - (\(\ref{eq7.3.29}\)), la Ecuación (9.5.9) se convierte en:

\[\right (\dfrac{T_0}{m} -\mu_r g \right) + \dfrac{(\rho S (\mu_r C_L - C_D) - 2T_0 k)}{2m} V^2 = V.\label{eq7.3.32}\]

Ahora, tenemos que integrar Equation (\(\ref{eq7.3.32}\)).

Para ello, como se refiere el comunicado:\(T_0, m, \mu_r, g, \rho, S, C_L, C_D\) y\(k\) puede considerarse constante a lo largo de la fase de despegue.

Tenemos que:

\[\dfrac{dV}{dt} = \dfrac{dV}{dx} \dfrac{dx}{dt},\]

y sabiendo eso\(\tfrac{dx}{dt} = V\), la ecuación (\(\ref{eq7.3.32}\)) se convierte en:

\[\dfrac{(\tfrac{T_0}{m} - \mu_r g) + \tfrac{(\rho S (\mu_r C_L - C_D) - 2T_0 k)}{2m} V^2}{V} = \dfrac{dV}{dx}.\label{eq7.3.34}\]

Para simplificar la ecuación (\(\ref{eq7.3.34}\)):

• \((\tfrac{T_0}{m} - \mu_r g) = g(\tfrac{T_0}{mg} - \mu_r) = A;\)
• \(\tfrac{(\rho S (\mu_r C_L - C_D) - 2T_0 k)}{2m} = B.\)

Se procede a integrar la Ecuación (\(\ref{eq7.3.34}\)) entre\(x = 0\) y\(x_{T0}\) (la distancia de despegue);\(V = 0\) (Suponiendo que la maniobra se inicia con la aeronave en reposo) y la velocidad de despegue que se dio en el enunciado:\(V_{TO} = 70\ m/s\). Sostiene que:

\[\int_{0}^{x_{TO}} dx = \int_{0}^{V_{TO}} \dfrac{VdV}{A+ BV^2}.\]

Integrando:

\[\left [ x \right ]_{0}^{x_{TO}} = \left [ \dfrac{1}{2B} \ln (A + BV^2) \right ]_{0}^{V_{TO}}.\]

Sustituyendo los límites superior e inferior:

\[x_{TO} = \dfrac{1}{2B} \ln (1 + \dfrac{B}{A} V_{TO}^2).\]

Sustituyendo los datos que figuran en el enunciado:

• \(A = 1.31725 \tfrac{m}{s^2};\)
• \(B = -3.69 \cdot 10^{-5} \tfrac{m}{s^2};\)
• \(V_{TO} = 70\ m/s.\)

La distancia a despegar es\(x_{TO} = 2000\ m\).

Ejercicio\(\PageIndex{3}\) Performances

Una aeronave tiene las siguientes características:

• \(S_w = 130\ m^2\).
• \(b = 40\ m\).
• \(m = 70000\ kg\).
• \(T_{\max, av} (h = 0) = 120000\ N\)(Empuje máximo disponible a nivel del mar).
• \(C_{D_0} = 0.02\).
• Coeficiente de Oswald (coeficiente de eficiencia del ala):\(e = 0.9\).
• \(C_{L_{\max}} = 1.5\).

Podemos considerar que el empuje máximo solo varía con la altitud de la siguiente manera:\(T_{\max, av} (h) = T_{\max, av} (h = 0) \tfrac{\rho}{\rho_0}\). Considera la atmósfera estándar\(ISA\) y la gravedad constante\(g = 9.8\ m/s^2\). Determinar:

1. El empuje requerido para volar a una altitud de\(h = 11000\ m\) con\(M_{\infty} = 0.7\) en vuelo horizontal, constante, recto.

2. La velocidad máxima debido a limitaciones de propulsión de la aeronave y el número de Mach correspondiente en vuelo horizontal, constante, recto a\(h = 11000\).

3. La velocidad mínima debido a limitaciones aerodinámicas (velocidad de calado) en horizontal, constante, vuelo recto a una altitud de\(h = 11000\).

4. El techo teórico (altitud máxima) en vuelo horizontal, constante, recto.

Queremos realizar un giro horizontal a una altitud de\(h = 11000\) con un factor de carga\(n = 2\), y con la velocidad correspondiente a la máxima eficiencia aerodinámica en vuelo horizontal, estable, recto. Determinar:

5. El ángulo de inclinación requerido.

6. El radio de giro.

7. El empuje requerido. ¿Puede la aeronave realizar el giro completo?

Queremos realizar un giro horizontal con el mismo factor de carga y el mismo radio que en el caso anterior, pero a una altitud correspondiente al techo teórico de la aeronave.

8. ¿Puede el avión realizar tal giro?

Contestar

Además de los datos dados en el enunciado, se han utilizado los siguientes datos:

• \(R = 287\ J/(kgK)\).
• \(\gamma_{air} = 1.4.\)
• \(\alpha_T = 6.5 \cdot 10^{-3} \ K/m\).
• \(\rho_0 = 1.225 \ kg/m^3\).
• \(T_0 = 288.15\ K\).
• \(ISA: \rho = \rho_0 (1 - \tfrac{\alpha_T h}{T_0})^{\tfrac{gR}{\alpha_T} - 1}.\)

1. Empuje requerido para volar un vuelo horizontal, estable y recto bajo las siguientes condiciones de vuelo:
   \(\bullet\)\(h = 11.000\ m\);
   \(\bullet\)\(M_{\infty} = 0.7.\)
   De acuerdo con\(ISA\):
   \(\bullet\)\(\rho (h = 11000) = 0.364\ Kg/m^3\);
   \(\bullet\)\(a (h = 11000) = \sqrt{\gamma_{air} R (T_0 - \alpha_T h)} = 295.04\ m/s\).
   donde a corresponde a la velocidad del sonido.
   El sistema que gobierna la dinámica de la aeronave es:
   \[T = D;\label{eq7.3.37}\]
   \[L = mg;\label{eq7.3.38}\]
   ser\(L\) el elevador,\(mg\) el peso;\(T\) la confianza y\(D\) el arrastre.
   Es bien sabido que:
   \[L = C_L \dfrac{1}{2} \rho S_w V^2;\label{eq7.3.39}\]
   \[D = C_D \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.40}\]
   También es bien sabido que el coeficiente de arrastre puede expresarse en forma parabólica de la siguiente manera:
   \[C_D = C_{D_0} + C_{D_i} C_L^2,\label{eq7.3.41}\]
   donde \(C_{D_0}\)se da en el comunicado y\(C_{D_i} = \tfrac{1}{\pi A e}\). La ampliación,\(A\), se puede calcular como\(A = \tfrac{b^2}{S_w} = 12.30\) y por lo tanto:\(C_{D_i} = 0.0287\).
   Según la Ecuación (\(\ref{eq7.3.38}\)):\(L = 686000\ N\). La velocidad de vuelo se puede calcular como\(V = M_{\infty} a = 206.5\ m/s\). Una vez obtenidos estos valores, con los valores de densidad y superficie húmeda, y entrando en la Ecuación (\(\ref{eq7.3.39}\)), los obtenemos\(C_L = 0.68\).
   Con los valores de\(C_L\),\(C_{D_i}\), y\(C_{D_0}\), entrando en la Ecuación (\(\ref{eq7.3.41}\)) obtenemos eso\(C_D = 0.0332\).
   Mirando ahora a la Ecuación (\(\ref{eq7.3.37}\)) y usando la Ecuación (\(\ref{eq7.3.40}\)), podemos afirmar que el empuje requerido es el siguiente:
   \[T = C_D \dfrac{1}{2} \rho S_w V^2.\nonumber\]
   Dado que todos los valores son conocidos, el empuje requerido rinde:
   \[T = 33567\ N.\nonumber\]
   Antes de seguir adelante, debemos mirar si el empuje requerido excede o no el empuje máximo disponible a la altitud dada. Para ello, se ha dado que el empuje máximo solo varía con la altitud de la siguiente manera:
   \[T_{\max, av} (h) = T_{\max, av} (h = 0) \dfrac{\rho}{\rho_0}.\]
   El empuje máximo disponible a\(h = 11000\) rendimientos:
   \[T_{\max, av} (h = 11000) = 35657.14\ N.\label{eq7.3.43}\]
   Desde\(T < T_{\max, av}\), el vuelo la condición es volable.
2. La velocidad máxima debido a limitaciones propulsivas de la aeronave y el número Mach correspondiente es horizontal, constante, vuelo recto a\(h = 11000\):
   La velocidad máxima debido a la limitación de propulsión a la altitud dada implica volar al máximo empuje disponible que se obtuvo en la Ecuación (\(\ref{eq7.3.43}\)).
   Mirando de nuevo a la Ecuación (\(\ref{eq7.3.37}\)) y usando la Ecuación (\(\ref{eq7.3.40}\)), podemos afirmar que:
   \[T_{\max, av} = C_D \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.44}\]
   Usando la Ecuación (\(\ref{eq7.3.41}\)) y la Ecuación (\(\ref{eq7.3.39}\)), y entrando en la Ecuación (\(\ref{eq7.3.44}\)) tenemos que:
   \[T_{\max, av} = \left ( C_{D_0} + C_{D_i} \left (\dfrac{L}{\tfrac{1}{2} \rho S_w V^2} \right )^2 \right ) \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.45}\]
   Multiplicando la Ecuación (\(\ref{eq7.3.45}\)) por\(V^2\) obtenemos una ecuación cuadrática de la forma:
   \[ax^2 + bx + c = 0.\]
   dónde\(x = V^2\),\(a = \tfrac{1}{2} \rho S_w C_{D_0}\),\(b = -T_{\max, av}\), y\(c = \dfrac{C_{D_i} L^2}{\tfrac{1}{2} \rho S_w}\).
   Resolviendo la ecuación cuadrática obtenemos dos velocidades diferentes a las que la aeronave puede volar dado el empuje máximo disponible ¹⁰. Esas velocidades rinden:
   \[V_1 = 228\ m/s;\nonumber\]
   \[V_2 = 151\ m/s.\nonumber\]
   El máximo corresponde, obviamente, a\(V_1\).
3. La velocidad mínima debido a limitaciones aerodinámicas (velocidad de calado) en horizontal, constante, vuelo recto a altitde de\(h = 11000\).
   La velocidad de calado se produce cuando el coeficiente de sustentación es máximo, por lo tanto, usando la ecuación (\(\ref{eq7.3.39}\)), tenemos que:
   \[V_{stall} = \sqrt{\dfrac{L}{\tfrac{1}{2} \rho S_w C_{L_{\max}}}} = 139\ m/s.\nonumber\]
4. El techo teórico (altitud máxima) en vuelo horizontal, constante, recto.
   Para obtener el techo teórico de la aeronave el empuje máximo disponible a esa altitud máxima debe coincidir con el empuje mínimo requerido para volar vuelo horizontal, estable, recto a esa altitud máxima, es decir:
   \[T_{\max, av} = T_{\min}.\label{eq7.3.47}\]
   Primero obtengamos el empuje mínimo requerido para volar vuelo horizontal, estable y recto. Multiplicando y dividiendo por\(L\) en el segundo término de la Ecuación (\(\ref{eq7.3.37}\)), y dado que la eficiencia aerodinámica es\(E = \tfrac{L}{D}\), tenemos que:
   \[T = \dfrac{D}{L} L = \dfrac{L}{E}.\]
   Dado que\(L\) es constante en esas condiciones de vuelo, se produce el empuje mínimo requerido cuando la eficiencia es máxima:\(T_{\min} \Leftrightarrow E_{\max}\).
   Procedamos ahora deduciendo la máxima eficiencia aerodinámica:
   La eficiencia aerodinámica se define como:
   \[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq7.3.49}\]
   Sustituir la curva polar parabólica dada en la Ecuación (\(\ref{eq7.3.41}\)) en la Ecuación (\(\ref{eq7.3.49}\)) , obtenemos:
   \[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\label{eq7.3.50}\]
   Para buscar los valores correspondientes a la máxima eficiencia aerodinámica, se debe derivar y hacerla igual a cero, es decir:
   \[\dfrac{dE}{dC_L} = 0 \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} + C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\label{eq7.3.51}\]
   Sustituyendo el valor de\(C_{L_{opt}}\) en Ecuación (\(\ref{eq7.3.50}\)) y simplificando obtenemos que:
   \[E_{\max} = \dfrac{1}{2\sqrt{C_{D_0} C_{D_i}}}.\nonumber\]
   \(E_{\max}\) rendimientos 20.86, y\(T_{\min} = 32870\ N\).
   De acuerdo con la Ecuación (\(\ref{eq7.3.43}\)) y basado en la Ecuación (\(\ref{eq7.3.47}\)) con\(T_{\min} = 32870\ N\), tenemos que:
   \[32870 = T_{\max, av} (h = 0) \dfrac{\rho}{\rho_0}.\nonumber\]
   Dado que\(T_{\max, av} (h = 0)\) se dio en el enunciado y\(\rho_0\) se sabe de acuerdo a\(ISA\), tenemos que \(\rho = 0.335\ kg/m^3\).
   Ya que\(\rho_{h_{\max}} < \rho_{11000}\) podemos deducir fácilmente que el eiling pertenece a la estratosfera. Usando la\(ISA\) ecuación correspondiente a la estratosfera tenemos eso:
   \[\rho_{h_{\max}} = \rho_{11} \exp^{-\tfrac{g}{TR_{11}} (h_{\max} - h_{11})}.\label{eq7.3.52}\]
   donde el subíndice 11 corresponde a los valores en la tropopausa\((h = 11000\ m)\). Operando en la Ecuación (\(\ref{eq7.3.52}\)), el techo rinde\(h_{\max} = 11526\ m\).
5. El ángulo de inclinación requerido:
   Las ecuaciones que rigen la dinámica del avión en un giro horizontal son:
   \[T = D;\label{eq7.3.53}\]
   \[m V \dot{\chi} = L \sin \mu;\label{eq7.3.54}\]
   \[L \cos \mu = mg.\label{eq7.3.55}\]
   En un movimiento circular uniforme (estacionario), es bien sabido que la velocidad tangencial es igual a la velocidad angular (\(\dot{\chi}\)) multiplicada por el radio o turn (\(R\)):
   \[V = \dot{\chi} R.\]
   Por lo tanto, Sytem (\(\ref{eq7.3.53}\),\(\ref{eq7.3.54}\) y\(\ref{eq7.3.55}\)) se puede reescribir como:
   \[T = D;\label{eq7.3.57}\]
   \[n \sin \mu = \dfrac{V^2}{gR};\label{eq7.3.58}\]
   \[n = \dfrac{1}{\cos \mu};\label{eq7.3.59}\]
   donde\(n = \tfrac{L}{mg}\) está el factor de carga.
   Por lo tanto, al observar la Ecuación (\(\ref{eq7.3.59}\)), es sencillo determinar que el ángulo de giro de inclinación es\(\mu = 60^{\circ}\).
6. El radio de giro.
   Primero, necesitamos calcular la velocidad correspondiente a la máxima eficiencia. Como hemos calculado antes en la Ecuación (\(\ref{eq7.3.51}\)), el coeficiente de sustentación que genera la máxima eficiencia es el denominado coeficiente óptimo de sustentación, es decir,\(C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}} = 0.834\). La velocidad rinde entonces:
   \[V = \sqrt{\dfrac{L}{\tfrac{1}{2} \rho S_w C_{L_{opt}}}} = 186.4\ m/s.\nonumber\]
   Entrando en la Ecuación (\(\ref{eq7.3.58}\)) con\(\mu = 60\ [deg]\) y\(V = 186.4\ m/s\);\(R = 4093.8\ m\).
7. El empuje requerido.
   Como se expone en la Pregunta 3, la Ecuación (\(\ref{eq7.3.57}\)) se puede expresar como:
   \[T = \dfrac{1}{2} \rho S_w V^2 C_{D_0} + \dfrac{L^2}{\tfrac{1}{2} \rho V^2 S_w} C_{D_i}.\nonumber\]
   Dado que todos los valores son conocidos:\(T = 32451\ N\)
   Desde\(T \le T_{\max, av} (h = 110000)\), la aeronave puede realizar el giro.
8. Queremos realizar un giro horizontal con el mismo factor de carga y el mismo radio que el caso permeable, pero a una altitud correspondiente al techo tearético de la aeronave. ¿El avión puede realizar el giro?
   Si el factor de carga es el mismo,\(n = 2\), necesariamente (según la Ecuación (\(\ref{eq7.3.59}\)) el ángulo de inclinación es el mismo,\(\mu = 60^{\circ}\). También, si el radio de giro es el mismo,\(R = 4093.8\ m\), necesariamente (según la Ecuación (\(\ref{eq7.3.58}\)), la velocidad del giro debe ser la misma que en el caso anterior,\(V = 186.4\ m/s\). Obviamente, dado que la densidad cambiará según la nueva altitud (\(\rho = 0.335\ kg/m^3\)), el giro no se realizará bajo condiciones de máxima eficiencia.
   Para saber cuálse puede realizar el giro o no, debemos comparar el empuje requerido con el empuje máximo disponible a la altitud del techo:
   \[T = \dfrac{1}{2} \rho S_w V^2 C_{D_0} + \dfrac{L^2}{\tfrac{1}{2} \rho V^2 S_w} C_{D_i} = 32983\ N.\nonumber\]
   \[T_{\max, av} (h = 11526) = T_{\max, av} (h = 0) \dfrac{\rho}{\rho_0} = 32816\ N.\nonumber\]
   Ya que\(T > T_{\max, av}\) en el techo, el giro no se puede realizar.

Ejercicio\(\PageIndex{4}\) Weights

Considera un Airbus A-320. Simplificando, asumimos que el ala de la aeronave es rectangular y está compuesta sobre perfiles NACA 4415. Las características de los perfiles aerográficos NACA 4415 son las siguientes:

• \(c_l = 0.2 + 5.92 \alpha\). (\(\alpha\)en radianes).
• \(c_d = 6.4 \cdot 10^{-3} - 1.2 \cdot 10^{-3} c_l + 3.5 \cdot 10^{-3} c_l^2\).

En cuanto a la aeronave, se conocen los siguientes datos:

• Superficie húmeda del ala de 122.6\([m^2]\).
• Ala-lapso de 34.1\([m]\).
• Factor de eficiencia de Oswald de 0.95.
• Consumo específico por unidad de empuje y tiempo:\(\eta_j = 6.8 \cdot 10^{-5} [\tfrac{Kg}{N \cdot s}]\).

Calcular:

1. La elevación del ala en su rango lineal.
2. La curva polar de arrastre, asumiendo que se puede expresar como:\(C_D = C_{D_0} + C_{D_i} C_L^2\).
3. El coeficiente óptimo de elevación del ala,\(C_{L_{opt}}\). Compárela con la del perfil aerodinámica.

En cuanto a los pesos característicos de la aeronave, se conocen los siguientes datos:

• Peso operativo vacío\(OEW = 42.4\ [Ton]\).
• Peso máximo de despegue\(MTOW = 77000 \cdot g\ [N]\) ¹¹.
• Peso máximo de combustible\(MFW = 29680 \cdot g\ [N]\).
• Peso máximo de combustible cero\(MZFW = 59000 \cdot g\ [N]\).
• Más aún, el combustible de reserva (\(RF\)) se puede calcular como el 5% del combustible de viaje (\(TF\)).

Calcular:

4. La Carga Útil y el Combustible de Viaje en los siguientes casos:

(a) Peso inicial igual al\(MTOW\) de la Carga Útil Máxima\((MPL)\).
(b) Peso inicial igual al\(MTOW\) Peso Máximo de Combustible\((MFW)\).
c) Peso inicial igual a\(OEW\) más\(MFW\).

Suponiendo que en condiciones de crucero la aeronave vuela a altitud constante\(h = 11500\ [m]\)\(M = 0.78\), número de Mach constante y máxima eficiencia aerodinámica, considerando la atmósfera\(ISA\) estándar, calcula:

5. Alcance y autonomía de la aeronave para los tres pesos iniciales señalados anteriormente.

6. De acuerdo con los resultados obtenidos, dibuje el diagrama de rango de carga útil.

Contestar

1. Curva de sustentación del ala:
   La curva de sustentación de un ala se puede expresar de la siguiente manera:
   \[C_L = C_{L_0} + C_{L_{\alpha}} \alpha,\label{eq7.3.60}\]
   y la pendiente de la curva de sustentación del ala se puede expresar relacionada con la pendiente de la curva de sustentación del ala como:
   \[C_{L_{\alpha}} = \dfrac{C_{l_{\alpha}}}{1 + \tfrac{C_{l_{\alpha}}}{\pi A}} e = 4.69 \cdot 1/rad.\nonumber\]
   Para calcular el término independiente de la curva de sustentación del ala, debemos considerar el hecho de que el ángulo de ataque de levantamiento cero del ala coincide con el ángulo de ataque de cero sustentación del ala, es decir:
   \[\alpha (L = 0) = \alpha (l = 0).\label{eq7.3.61}\]
   Primero, observe que la curva de elevación de un perfil aerodinámico se puede expresar de la siguiente manera
   \[C_l = C_{l_0} + C_{l_{\alpha}} \alpha.\label{eq7.3.62}\]
   Por lo tanto, con la Ecuación (\(\ref{eq7.3.60}\)) y la Ecuación (\(\ref{eq7.3.61}\)\(\ref{eq7.3.62}\)) en la Ecuación (), tenemos que:
   \[C_{L_0} = C_{l_0} \dfrac{C_{L_{\alpha}}}{C_{l_{\alpha}}} = 0.158.\nonumber\]
   La curva requerida rinde entonces:
   \[C_L = 0.158 + 4.69 \alpha \ [\alpha \ in\ rad].\nonumber\]
2. La expresión del polar parabólico del ala:
   Observe primero que la afirmación del problema indica que el polar debe estar en la siguiente forma:
   \[C_D = C_{D_0} + C_{D_i} C_L^2.\label{eq7.3.63}\]
   Para el cálculo de la resistencia parabólica del ala podemos considerar el término parásito aproximadamente igual al término parásito del perfil aerodinámico, es decir,\(C_{D_0} = C_{d_0}\).
   El coeficiente de arrastre inducido se puede calcular de la siguiente manera:
   \[C_{D_i} = \dfrac{1}{\pi Ae} = 0.035.\nonumber\]
   La expresión de los rendimientos polares parabólicos entonces:
   \[C_D = 0.0064 + 0.035 C_L^2.\]
3. El coeficiente óptimo de sustentación,\(C_{L_{opt}}\), para el ala. Compárelo con el de los perfiles aerográficos.
   El coeficiente óptimo de elevación es el que hace que la eficiencia aerodinámica sea máxima. La eficiencia aerodinámica se define como:
   \[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq7.3.65}\]
   Sustituyendo la curva polar parabólica dada en la Ecuación (\(\ref{eq7.3.63}\)) en la Ecuación (\(\ref{eq7.3.65}\)), obtenemos:
   \[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\label{eq7.3.66}\]
   Para buscar los valores correspondientes a la máxima eficiencia aerodinámica, se debe derivar y hacerla igual a cero, es decir:
   \[\dfrac{dE}{dC_L} = 0 = \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} - C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\label{eq7.3.67}\]
   Para el caso de un perfil aerodinámico, la eficiencia aerodinámica se define como:
   \[E = \dfrac{l}{d} = \dfrac{c_l}{c_d}.\label{eq7.3.68}\]
   Sustituyendo el polar parabólico curva dada en el enunciado en la forma\(c_{d_0} + bc_l + kc_l^2\) en la Ecuación (\(\ref{eq7.3.68}\)), obtenemos:
   \[E = \dfrac{c_l}{c_{d_0} + bc_l + kc_l^2}.\]
   Para buscar los valores correspondientes a la máxima eficiencia aerodinámica, se debe derivar y hacerla igual a cero, es decir:
   \[\dfrac{dE}{dC_l} = 0 = \dfrac{c_{d_0} - kc_l^2}{(c_{d_0} + bc_l + kc_l^2)^2} \to (c_l)_{E_{\max}} = (c_l)_{opt} = \sqrt{\dfrac{c_{d_0}}{k}}.\label{eq7.3.70}\]
   De acuerdo con los valores previamente obtenidos (\(C_{D_0} = 0.0064\)y\(C_{D_i} = 0.035\)) y los valores dados en el enunciado para el polar (\(c_{d_0} = 0.0064\),\(k = 0.0035\)) del perfil aerodinámico, sustituyéndolos en la Ecuación (\(\ref{eq7.3.67}\)) y Ecuación (\(\ref{eq7.3.70}\)), respectivamente, obtenemos:
   \(\bullet\)\((C_L)_{opt} = 0.42;\)
   \(\bullet\)\((c_l)_{opt} = 1.35.\)
4. Carga útil y Combustible de Viaje para los casos (a), (b), y (c):
   Antes de iniciar nosotros los casos particulares, es necesario señalar que:
   \[TOW = OEW + PL + FW,\label{eq7.3.71}\]
   \[FW = TF + RF,\label{eq7.3.72}\]
   \[MZFW = OEW + MPL.\label{eq7.3.73}\]
   Por otra parte, según la declaración,
   \[RF = 0.05 \cdot TF.\]
   Con base en los datos dados en el enunciado, y usando la Ecuación (\(\ref{eq7.3.73}\)):
   \[MPL = 16.6\ [Ton.].\]
   Caso (a) Peso inicial ¹²\(\to\)\(MTOW\) con\(MPL\).
   La ecuación (\(\ref{eq7.3.71}\)) se convierte en:
   \[MTOW = OEW + MPL + TF + 0.05 \cdot TF,\label{eq7.3.76}\]
   Aislamiento en la ecuación (\(\ref{eq7.3.76}\)):\(TF = 17.14\ [Ton]\). La carga útil es igual a la carga útil máxima\(MPL\).
   Caso (b) Peso inicial\(\to\)\(MTOW\) con\(MFW\).
   La ecuación (\(\ref{eq7.3.71}\)) se convierte en:
   \[MTOW = OEW + PL + MFW,\label{eq7.3.77}\]
   Aislamiento en la ecuación (\(\ref{eq7.3.77}\)):\(PL = 4.92\ [Ton]\). Para calcular el combustible de viaje, mirando la Ecuación (\(\ref{eq7.3.72}\)), tenemos que
   \[MFW = TF + RF = TF + 0.05 \cdot TF.\]
   Aislar,\(TF = 28.266\ [Ton.]\).
   Caso (c) Peso inicial\(\to\)\(OEW + MFW\).
   La ecuación (\(\ref{eq7.3.71}\)) se convierte en:
   \[TOW = OEW + MFW,\]
   Eso significa que\(PL = 0\), para calcular el combustible de viaje, procedemos exactamente como en el Caso (b). Mirando la Ecuación (\(\ref{eq7.3.72}\)), tenemos que
   \[MFW = TF + RF = TF + 0.05 \cdot TF.\]
   Aislar,\(TF = 28.266\ [Ton.]\)
5. Alcance y Resistencia para los casos (a), (b) y (c): Considerando que la aeronave realiza un vuelo lineal y horizontal constante, tenemos que:
   \[L = mg;\label{eq7.3.81}\]
   \[T = D;\label{eq7.3.82}\]
   \[\dot{x} = V;\label{eq7.3.83}\]
   \[\dot{m} = -\eta T.\label{eq7.3.84}\]
   Ya que\(\dot{x} = \tfrac{dx}{dt}\), es claro que el Rango\(R\), al mirar la Ecuación (\(\ref{eq7.3.83}\)), se puede expresar como:
   \[R = \int_{t_i}^{t_f} V dt.\label{eq7.3.85}\]
   Ahora, ya que\(\dot{m} = \tfrac{dm}{dt} = -\eta T\), Ecuación (\(\ref{eq7.3.85}\)):
   \[R = \int_{m_i}^{m_f} -\dfrac{V}{\eta T} dm,\label{eq7.3.86}\]
   dónde\(m_i\) está la masa inicial y\(m_f\) es la masa final.
   Usando la ecuación (\(\ref{eq7.3.81}\)) y la ecuación (\(\ref{eq7.3.82}\)), la ecuación (\(\ref{eq7.3.86}\)) produce:
   \[R = \int_{m_i}^{m_f} - \dfrac{VE}{\eta g} \dfrac{dm}{m}.\]
   con\(E = \tfrac{L}{D}, V, \eta\), y\(g\) son valores constantes.
   Integrando:
   \[R = \dfrac{VE}{\eta g} \ln (\dfrac{m_i}{m_f}).\label{eq7.3.88}\]
   Para la resistencia, operamos de manera análoga, integrando la Ecuación (\(\ref{eq7.3.84}\)), que rinde
   \[t = \int_{m_i}^{m_f} - \dfrac{1}{\eta T} dm.\label{eq7.3.89}\]
   Usando la Ecuación (\(\ref{eq7.3.81}\)) y (\(\ref{eq7.3.82}\)), ( \(\ref{eq7.3.89}\)) rinde:
   \[t = \int_{m_i}^{m_f} - \dfrac{E}{\eta g} \dfrac{dm}{m}.\]
   donde otra vez\(E = \tfrac{L}{D}\),\(\eta\) y\(g\) son valores constantes. Integración:
   \[t = \dfrac{E}{\eta g} \ln (\dfrac{m_i}{m_f}).\label{eq7.3.91}\]
   Antes de calcular Rango y Resistencia para los tres casos, necesitamos calcular los valores de velocidad y eficiencia aerodinámica, que es máxima.
   La velocidad se puede expresar como\(V = M \cdot a\), donde\(a\) esta la velocidad del sonido, que se puede expresar como
   \[a = \sqrt{\gamma RT},\]
   donde\(\gamma = 1.4\) es coeficiente adiabatico del aire, y\(R = 287\ J/KgK\) es la constante de gas perfecta. Observe que, utilizando\(ISA\), la temperatura en la estratosfera es constante, y así\(T = 216.6\ K\).
   Sustituyendo todos los términos, rinde\(v = 230.1\ [m/s]\).
   La eficiencia aerodinámica es máxima. Así, sustituyendo\(C_{L_{opt}}\) obtenida en la Ecuación (\(\ref{eq7.3.67}\)) por la Ecuación (\(\ref{eq7.3.66}\)), produce:
   \[E = \dfrac{1}{2\sqrt{C_{D_0} C_{D_i}}} = 33.4.\]
   Ahora, debemos calcular la masa inicial y final para de los tres casos a), b), c). Observe que la masa final resulta de restar el combustible de disparo de la masa de despegue:
   \[m_f = m_i - TF.\]
   Así,
   (a)\(m_i = \dfrac{MTOW}{g} [Kg]\) y\(m_f = 59860\ [Kg]\).
   b)\(m_i = \dfrac{MTOW}{g} [Kg]\) y\(m_f = 48734\ [Kg]\).
   (c)\(m_i = 72080 [Kg]\) y\(m_f = 43814\ [Kg]\).
   Sustituyendo en la Ecuación (\(\ref{eq7.3.88}\)) y Ecuación (\(\ref{eq7.3.91}\)), produce:
   (a)\(R_a = 2900\ [Km]\) y\(t_a = 12600\ [s]\).
   b)\(R_b = 5270\ [Km]\) y\(t_b = 22900\ [s]\).
   (c)\(R_c = 5736\ [Km]\) y\(t_c = 24928\ [s]\).
6. Casos de diagrama de rango de carga de pago (a), (b) y (c):
   
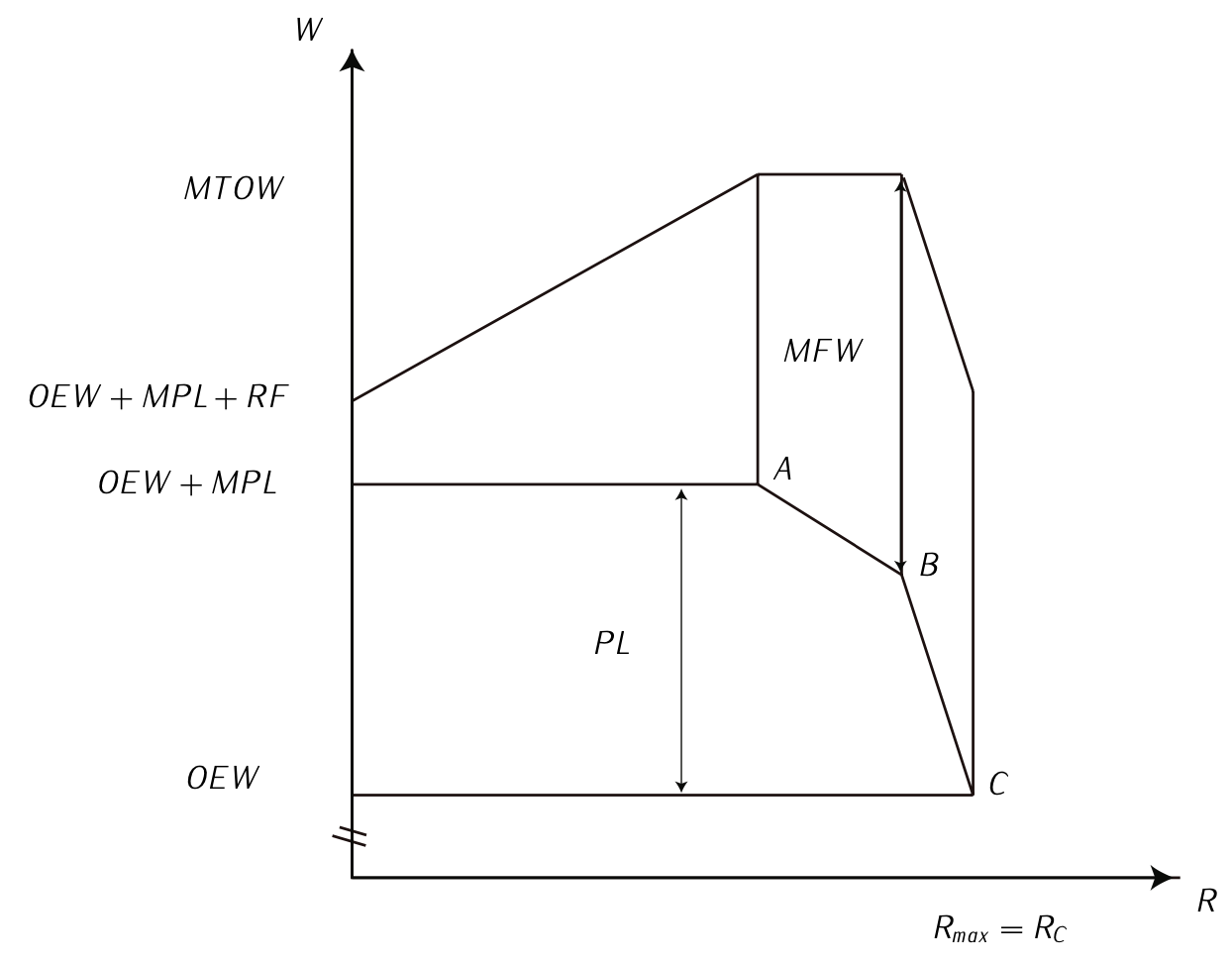
   Figura 7.17: Diagrama de rango de carga de pago

Ejercicio\(\PageIndex{5}\)

Una aeronave tiene las siguientes características:

• \(S_w = 130\ m^2\).
• \(b = 40\ m\).
• \(m = 70000\ kg\).
• \(T_{\max, av, 0} = 130000\ N\)(Empuje máximo disponible a nivel del mar).
• \(C_{D_0} = 0.02\).
• Factor de eficiencia de Oswald:\(e = 0.9\).

Se puede considerar que el empuje máximo disponible varía de acuerdo con la siguiente ley:

\[T_{\max, av} (h) = T_{\max, av, 0} \dfrac{\rho}{\rho_0}.\nonumber\]

Considera\(ISA\) la atmósfera y la gravedad constante\(g = 9.8\ m/s^2\). Determinar:

1. El empuje requerido para volar a una altitud de\(h = 11250\ m\) at\(M_{\infty} = 0.78\) en vuelo lineal-horizontal constante.
2. La velocidad máxima de la aeronave debido a limitaciones de propulsión en vuelo lineal-horizontal constante a una altitud de\(h = 11250\ m\).
3. El techo teórico de la aeronave en vuelo lineal-horizontal constante.

Ahora queremos detereminar la superficie del estabilizador horizontal y como criterio de diseño tomamos las condiciones de vuelo de equilibrio a una altitud de\(h = 11250\ m\) &\(M_{\infty} = 0.78\). En esas condiciones, el coeficiente de sustentación del estabilizador es igual a 1.4. Además, podemos suponer que la distribución de sustentación del ala puede reducirse a una fuerza resultante en el centro aerodinámico (elevación) y un momento de cabeceo hacia abajo con respecto al centro aerodinámico igual a\(10000\ N \cdot m\). La distancia entre el centro aerodinámico y el centro de gravedad (tenga en cuenta que el centro aerodinámico está más cerca de la nariz de la aeronave) es\(x_{cg} = 2\ m\). La distancia entre el estabilizador y el centro de gravedad es\(l = 20\ m\).

4. Determinar la superficie del estabilizador horizontal para esas condiciones de vuelo.

Contestar

Además de los datos dados en el enunciado, se han utilizado los siguientes datos:

• \(R = 287\ J/(kgK)\).
• \(\gamma_{air} = 1.4\).
• \(T_{11} = 216.6\ K\).
• \(\rho_{11} = 0.36\ kg/m^3\).
• \(T_0 = 288.15\ K\).
• \(ISA: \rho = \rho_{11} \cdot e^{\tfrac{-gR}{T_{11}}} (h - 11000)\).

1. Empuje requerido para volar un vuelo horizontal, constante, recto bajo las siguientes condiciones de vuelo:
   \(\bullet\)\(h = 11.250\ m\).
   \(\bullet\)\(M_{\infty} = 0.78\).
   Según\(ISA\):
   \(\bullet\)\(\rho (h = 11250) = 0.3461\ Kg/m^3\).
   \(\bullet\)\(a (h = 11250) = \sqrt{\gamma_{air} R(T_{11})} = 295\ m/s\).
   donde a corresponde a la velocidad del sonido.
   El sistema que gobierna la dinámica de la aeronave es:
   \[T = D,\label{eq7.3.95}\]
   \[L = mg,\label{eq7.3.96}\]
   ser\(L\) el elevador,\(mg\) el peso;\(T\) la confianza y\(D\) el arrastre.
   Es bien sabido que:
   \[L = C_L \dfrac{1}{2} \rho S_w V^2;\label{eq7.3.97}\]
   \[D = C_D \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.98}\]
   También es bien sabido que el coeficiente de arrastre puede expresarse en forma prabólica de la siguiente manera:
   \[C_D = C_{D_0} + C_{D_i} C_L^2,\label{eq7.3.99}\]
   donde \(C_{D_0}\)se da en el comunicado y\(C_{D_i} = \tfrac{1}{\pi Ae}\). La ampliación se\(A\) puede calcular como\(A = \tfrac{b^2}{S_w} = 12.30\) y por lo tanto:\(C_{D_i} = 0.0287\).
   Según la Ecuación (\(\ref{eq7.3.96}\)):\(L = 686000\ N\). La velocidad de vuelo se puede calcular como\(V = M_{\infty} a = 230.1\ m/s\). Una vez obtenidos estos valores, con los valores de densidad y superficie húmeda, y entrando en la Ecuación (\(\ref{eq7.3.97}\)), los obtenemos\(C_L = 0.5795\).
   Con los valores de\(C_L, C_{D_i}\) y\(C_{D_0}\), entrando en la Ecuación (\(\ref{eq7.3.99}\)) obtenemos eso\(C_D = 0.0295\).
   Mirando ahora a la Ecuación (\(\ref{eq7.3.95}\)) y usando la Ecuación (\(\ref{eq7.3.98}\)), podemos afirmar que el empuje requerido es el siguiente:
   \[T = C_D \dfrac{1}{2} \rho S_w V^2.\nonumber\]
   Dado que todos los valores son conocidos, el empuje requerido rinde:
   \[T = 35185\ N.\nonumber\]
   Antes de seguir adelante, debemos mirar si el empuje requerido excede o no el empuje máximo disponible a la altitud dada. Para ello, se ha dado que el empuje máximo solo varía con la altitud de la siguiente manera:
   \[T_{\max, av} (h) = T_{\max, av, 0} \dfrac{\rho}{\rho_0}.\label{eq7.3.100}\]
   El empuje máximo disponible a\(h = 11250\) rendimientos:
   \[T_{\max, av} (h = 11250) = 36729\ N.\label{eq7.3.101}\]
   Desde\(T < T_{\max, av}\), el vuelo la condición es volable.
2. La velocidad máxima debida a limitaciones propulsivas de la aeronave en vuelo horizontal, constante, recto a\(h = 11250\):
   La velocidad máxima debida a la limitación de propulsión a la altitud dada implica volar al empuje máximo disponible que se obtuvo en la Ecuación ( \(\ref{eq7.3.101}\)).
   Mirando a la ecuación (\(\ref{eq7.3.95}\)) y usando la ecuación (\(\ref{eq7.3.98}\)), podemos afirmar que:
   \[T_{\max, av} = C_D \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.102}\]
   Usando la ecuación (\(\ref{eq7.3.99}\)) y la ecuación (\(\ref{eq7.3.97}\)), y entrando en la ecuación (\(\ref{eq7.3.102}\)) tenemos que:
   \[T_{\max, av} = \left (C_{D_0} + C_{D_i} \left (\dfrac{L}{\tfrac{1}{2} \rho S_w V^2} \right )^2 \right ) \dfrac{1}{2} \rho S_w V^2.\label{eq7.3.103}\]
   Multiplicando la Ecuación (\(\ref{eq7.3.103}\)) por\(V^2\) obtenemos una ecuación cuadrática de la forma:
   \[ax^2 + bx + c = 0.\]
   dónde\(x = V^2\),\(a = \dfrac{1}{2} \rho S_w C_{D_0}, b = - T_{\max, av}\) y\(c = \dfrac{C_{D_i} L^2}{\tfrac{1}{2} \rho S_w}\).
   Resolviendo la ecuación cuadrática obtenemos dos velocidades diferentes a las que la aeronave puede volar dado el empuje máximo disponible13. Esas velocidades rinden:
   \[V_1 = 218\ m/s;\nonumber\]
   \[V_2 = 184.06\ m/s.\nonumber\]
   Las velocidades máximas corresponden, obviamente, a\(V_1\).
3. El techo teórico (altitud máxima) en vuelo horizontal, constante, recto.
   Para obtener el techo teórico de la aeronave el empuje máximo disponible a esa altitud máxima debe coincidir con el empuje mínimo requerido para volar vuelo horizontal, estable, recto a esa altitud máxima, es decir:
   \[T_{\max, av} = T_{\min}.\label{eq7.3.105}\]
   Primero obtengamos el empuje mínimo requerido para volar vuelo horizontal, estable y recto. Multiplicando y dividiendo por\(L\) en el segundo término de la Ecuación (\(\ref{eq7.3.95}\)), y dado que la eficiencia de la\(E = \tfrac{L}{D}\) aerodinamia es, tenemos que:
   \[T = \dfrac{D}{L} L = \dfrac{L}{E}.\]
   Dado que\(L\) es constante en esas condiciones de vuelo, se produce el empuje mínimo requerido cuando la eficiencia es máxima:\(T_{\min} \Leftrightarrow E_{\max}\).
   Procedamos ahora deduciendo la máxima eficiencia aerodinámica:
   La eficiencia aerodinámica se define como:
   \[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq7.3.107}\]
   Sustituyendo la curva polar parabólica gicen en Ecuación curva polar dada en Ecuación ( \(\ref{eq7.3.99}\)) en la Ecuación (\(\ref{eq7.3.107}\)), obtenemos:
   \[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\label{eq7.3.108}\]
   Para buscar los valores correspondientes a la máxima eficiencia aerodinámica, se debe derivar y hacerla igual a cero, es decir:
   \[\dfrac{dE}{dC_L} = 0 = \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} + C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\]
   Sustituyendo el valor de\(C_{L_{opt}}\) en Ecuación (\(\ref{eq7.3.108}\)) y simplificando obtenemos que:
   \[E_{\max} = \dfrac{1}{2\sqrt{C_{D_0} C_{D_i}}}.\nonumber\]
   \(E_{\max}\) rinde 20.86, y\(T_{\min} = 32904\ N\).
   De acuerdo con la Ecuación (\(\ref{eq7.3.101}\)) y basado en la Ecuación (\(\ref{eq7.3.105}\)) con\(T_{\min} = 32904\ N\), tenemos que:
   \[32904 = T_{\max, av, 0} \dfrac{\rho}{\rho_0}.\nonumber\]
   Dado que\(T_{\max, av, 0}\) se dio en el enunciado y\(\rho_0\) se sabe de acuerdo a\(ISA\), tenemos que \(\rho = 0.3101\ kg/m^3\).
   Ya que\(\rho_{h_{\max}} < \rho_{11000}\) podemos deducir fácilmente que el techo pertenece a la estratosfera. Usando la\(ISA\) ecuación correspondiente a la estratosfera tenemos eso:
   \[\rho_{h_{\max}} = \rho_{11} \exp^{-\tfrac{g}{RT_{11}} (h_{\max} - h_{11})}.\label{eq7.3.110}\]
   donde el subíndice 11 corresponde a los valores en la tropopausa\((h = 11000\ m)\). Operando en la Ecuación (\(\ref{eq7.3.110}\)), el techo rinde\(h_{\max} = 11946\ m\).
4. Queremos determinar la superficie del estabilizador horizontal:
   Para ello, indicamos las ecuaciones para el problema de balanceo longitudinal:
   \[mg - L - L_t = 0;\label{eq7.3.111}\]
   \[-M_{ca} + Lx_{cg} - L_t l = 0;\label{eq7.3.112}\]
   dónde\(L_t\) está el levantamiento generado por el estabilizador horizontal,\(M_{ca} = 10000\ Nm\) es el par de paso con respecto al centro aerodinámico,\(x_{cg} = 2\ m\) es la distancia entre el centro de gravedad y el centro aerodinámico, y\(l = 20\ m\) es la distancia entre el centro de gravedad y el centro aerodinámico de la horizontal estabilizador.
   Entrando en la Ecuación (\(\ref{eq7.3.111}\)), tenemos eso\(L = mg - L_t\). Sabiendo eso\(L_t = 0.5 \rho S_t V^2 C_L\), y sustituyendo en la Ecuación (\(\ref{eq7.3.112}\)), tenemos que:
   \[L_t = \dfrac{mg \cdot x_{cg} - M_{ca}}{l + x_{cg}} \to S_t = \dfrac{1}{0.5 \rho V^2 C_{L_t}} \dfrac{mg \cdot x_{cg} - M_{ca}}{l + x_{cg}} = 4.78\ m^2.\]

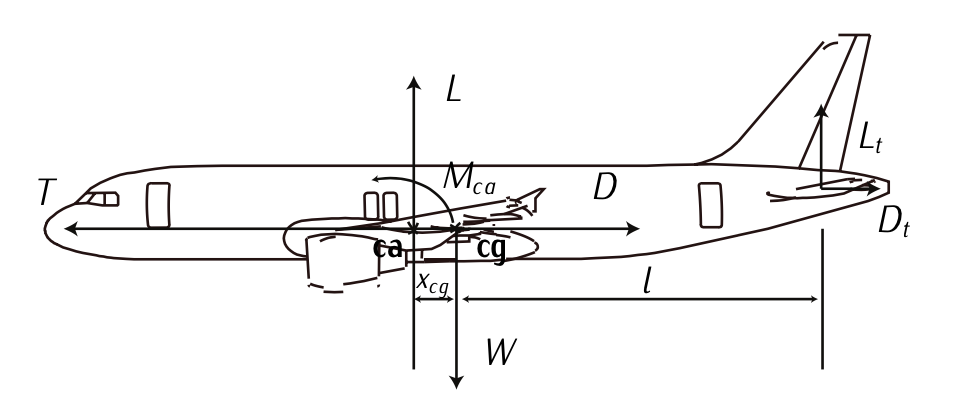
Figura 7.18: Equilibrio longitudinal.

Ejercicio\(\PageIndex{6}\) Performances

Considera un Airbus A-320 con las siguientes características:

• \(m = 64\)toneladas.
• \(S_w = 122.6\ m^2\)
• \(T_{\max, av, 0} = 130000\ N\)(empuje máximo disponible a nivel del mar).
• \(C_D = 0.024 + 0.0375 C_L^2\).

Se puede considerar que el empuje máximo disponible varía de acuerdo con la siguiente ley:

\[T_{\max, av} (h) = T_{\max, av, 0} \dfrac{\rho}{\rho_0}.\nonumber\]

Considera\(ISA\) la atmósfera y la gravedad constante\(g = 9.8\ m/s^2\).

1. El avión inicia una maniobra de ascenso uniforme (velocidad constante y ángulo de trayectoria de vuelo) a una altitud de 10.000 pies (\(3048\ m\)). A este nivel de vuelo, la velocidad aerodinámica es\(150\ m/s\) y la velocidad vertical es\(12\ m/s\). Asumiendo un pequeño ángulo de ataque\(\gamma \ll 1\), calcule:
   (a) El ángulo de trayectoria de vuelo de ascenso,\(\gamma\).
   b) El empuje requerido en estas condiciones.
   c) Razón ¹⁴ con respecto al empuje máximo disponible a esa altitud.
2. Calcular el ángulo máximo de ascenso (ángulo de trayectoria de vuelo) en ascenso uniforme a una altitud de 10000 pies. En estas condiciones, determinar:
   (a) La velocidad aerodinámica y la velocidad vertical.
3. Ahora queremos analizar las actuaciones de giro en el plano horizontal. Considere las condiciones del nivel del mar, la máxima eficiencia aerodinámica y las limitaciones estructurales caracterizadas por un factor de carga máximo de\(n_{\max} = 2.5\). En estas condiciones, calcule:
   (a) El ángulo de inclinación requerido.
   (b) Acelera un radio de giro.
   c) El empuje requerido.
   d) ¿Puede la aeronave realizar el giro completo?

Contestar

Además de los datos dados en el enunciado, se han utilizado los siguientes datos:

• \(g = 9.81\ m/s^2\).
• \(R = 287\ J/(kgK)\).
• \(\alpha_T = 6.5 \cdot 10^{-3}\ K/m\).
• \(\rho_0 = 1.225\ kg/m^3\).
• \(T_0 = 288.15\ K\).
• \(ISA: \rho = \rho_0 (1 - \dfrac{\alpha_T h}{T_0})^{\tfrac{gR}{\alpha_T} - 1}\).

1. Ascenso uniforme bajo las siguientes condiciones de vuelo:
   \(\bullet\)\(h = 3048\ m\). Usando\(ISA \to \rho = 0.904\ kg/m^3\).
   \(\bullet\)\(V = 150\ m/s\).
   \(\bullet\)\(\dot{h}_e = 12\ m/s\).
   El sistema que rige el movimiento de la aeronave es:
   \[T = D + mg \sin \gamma;\label{eq7.3.114}\]
   \[L = mg \cos \gamma;\label{eq7.3.115}\]
   \[\dot{x}_e = V \cos \gamma;\label{eq7.3.116}\]
   \[\dot{h}_e = V \sin \gamma.\label{eq7.3.117}\]
   Suponiendo que\(\gamma \ll 1\), y así eso\(\cos \gamma \sim 1\) y \(\sin \gamma \sim \gamma\), Sistema (\(\ref{eq7.3.114}\),,\(\ref{eq7.3.115}\)\(\ref{eq7.3.116}\),\(\ref{eq7.3.117}\)) se convierte en:
   \[T = D + mg \gamma;\label{eq7.3.118}\]
   \[L = mg;\label{eq7.3.119}\]
   \[\dot{x}_e = V;\label{eq7.3.120}\]
   \[\dot{h}_e = V_{\gamma}. \label{eq7.3.121}\]
   (a) De la Ecuación\(\ref{eq7.3.121}\),\(\gamma = \tfrac{\dot{h}_e}{V} = 0.08\ rad (4.58^{\circ})\).
   (b) De la Ecuación\(\ref{eq7.3.118}\),\(T = D + mg\gamma\).
   \[D = C_D \dfrac{1}{2} \rho S_w V^2,\label{eq7.3.122}\]
   donde\(C_D = 0.024 + 0.0375 C_L^2\), y\(\rho, S_w, V^2\) se conocen.
   \[C_L = \dfrac{L}{\tfrac{1}{2} \rho S_w V^2} = 0.5057.\label{eq7.3.123}\]
   donde, de acuerdo con la Ecuación (\(\ref{eq7.3.119}\)),\(L = mg\). Con la Ecuación (\(\ref{eq7.3.123}\)) en la Ecuación (\(\ref{eq7.3.122}\)),\(D = 41398\ N\).
   Finalmente:
   \[T = D + mg \gamma = 91886\ N.\nonumber\]
   (c) El empuje máximo en esas condiciones es
   \[T_{\max, av} (h = 3048) = T_{\max, av, 0} \dfrac{\rho}{\rho_0} = 95510\ N.\nonumber\]
   La relación es\(\sqcap = \tfrac{T}{T_{\max, av}} = 0.962\).
2. Ángulo máximo de ascenso.
   Consideramos nuevamente el conjunto de ecuaciones (\(\ref{eq7.3.118}\),\(\ref{eq7.3.119}\),\(\ref{eq7.3.120}\),\(\ref{eq7.3.121}\)). Ecuación de buceo (\(\ref{eq7.3.118}\)) por\(mg\), tenemos que:
   \[\gamma = \dfrac{T}{mg} - \dfrac{1}{E}.\]
   \(\gamma\) Para ser máximo:
   \(\bullet\)\(T = T_{\max, av} = 95510\ N\).
   \(\bullet\)\(E = E_{\max}\).
   Procedamos ahora deduciendo la máxima eficiencia aerodinámica:
   La eficiencia aerodinámica se define como:
   \[E = \dfrac{L}{D} = \dfrac{C_L}{C_D}.\label{eq7.3.125}\]
   Sustituyendo la curva polar parabólica dada en el enunciado de la Ecuación (\(\ref{eq7.3.125}\)), nosotros obtener:
   \[E = \dfrac{C_L}{C_{D_0} + C_{D_i} C_L^2}.\label{eq7.3.126}\]
   Para buscar los valores correspondientes a la máxima eficiencia aerodinámica, se debe derivar y hacerla igual a cero, es decir:
   \[\dfrac{dE}{dC_L} = 0 = \dfrac{C_{D_0} - C_{D_i} C_L^2}{(C_{D_0} - C_{D_i} C_L^2)^2} \to (C_L)_{E_{\max}} = C_{L_{opt}} = \sqrt{\dfrac{C_{D_0}}{C_{D_i}}}.\label{eq7.3.127}\]
   Sustituyendo el valor de\(C_{L_{opt}}\) en Ecuación (\(\ref{eq7.3.126}\)) y simplificación obtenemos que:
   \[E_{\max} = \dfrac{1}{2\sqrt{C_{D_0} C_{D_i}}}.\nonumber\]
   Sustituyendo:\(C_{L_{opt}} = 0.8, E_{\max} = 16.66\), y\(\gamma_{\max} = 5.27^{\circ}\).
   La velocidad aerodinámica estará dada por:
   \[V = \sqrt{\dfrac{m \cdot g}{\tfrac{1}{2} \rho S_w C_{L_{opt}}}} = 119\ m/s.\nonumber\]
   De la ecuación (\(\ref{eq7.3.117}\)),\(\dot{h}_e = V \cdot \gamma = 10.95\ m/s\).
3. Queremos realizar un giro horizontal a una altitud de\(h = 0\) con un factor de carga\(n = 2.5 = n_{\max}\), y con la velocidad correspondiente a la máxima eficiencia aerodinámica en vuelo horizontal, estable, recto.
   Las ecuaciones que rigen la dinámica del avión en un giro horizontal son:
   \[T = D;\label{eq7.3.128}\]
   \[mV \dot{\chi} = L \sin \mu;\label{eq7.3.129}\]
   \[L \cos \mu = mg.\label{eq7.3.130}\]
   En un movimiento circular uniforme (estacionario), es bien sabido que La velocidad tangencial es igual a la velocidad angular\(\dot{\chi}\) multiplicada por el radio de giro\(R\):
   \[V = \dot{\chi} R.\]
   Por lo tanto, System (\(\ref{eq7.3.128}\)\(\ref{eq7.3.129}\),,\(\ref{eq7.3.130}\)) se puede reescribir como:
   \[T = D;\label{eq7.3.132}\]
   \[n \sin \mu = \dfrac{V^2}{gR};\label{eq7.3.133}\]
   \[n = \dfrac{1}{\cos \mu};\label{eq7.3.134}\]
   donde\(n = \tfrac{L}{mg}\) está el factor de carga.
   a). El ángulo de inclinación requerido:
   Por lo tanto, al observar la ecuación (\(\ref{eq7.3.134}\)), es sencillo determinar que el ángulo de giro de inclinación es\(\mu = 66.4^{\circ}\).
   b). Velocidad y radio de giro.
   Primero, necesitamos c alcular la velocidad correspondiente a la máxima eficiencia. Como hemos calculado antes en la Ecuación (\(\ref{eq7.3.127}\)), el coeficiente de sustentación que genera la máxima eficiencia es el denominado coeficiente óptimo de sustentación, es decir,\(C_{L_{opt}} = \sqrt{\tfrac{C_{D_0}}{C_{D_i}}} = 0.8\). La velocidad rinde entonces:
   \[V = \sqrt{\dfrac{L}{\tfrac{1}{2} \rho_0 S_w C_{L_{opt}}}} = 161.57\ m/s.\nonumber\]
   Entrando en la Ecuación (\(\ref{eq7.3.133}\)) con\(\mu = 66.4\) [grados] y\(V = 161.57\ m/s\);\(R = 1167\ m\).
   c) El empuje requerido.
   La ecuación (\(\ref{eq7.3.132}\)) se puede expresar como:
   \[T = \dfrac{1}{2} \rho_0 S_w V^2 C_{D_0} + \dfrac{L^2}{\tfrac{1}{2} \rho_0 V^2 S_w} C_{D_i}.\nonumber\]
   Dado que todos los valores son conocidos:\(T = 94093\ N\)
   (d). Ya que\(T \le T_{\max, av} (h = 0)\), la aeronave puede realizar el giro.

---

9. Todas estas variables pueden considerarse constantes durante el despegue.

10. Observe que dada una altitud y un ajuste de empuje, la aeronave teóricamente puede volar a dos velocidades diferentes, mientras que esas velocidades se encuentran entre la velocidad mínima (pérdida) y una velocidad máxima (típicamente cerca de la velocidad de divergencia).

11. \(g\)representa la fuerza debida a la gravedad.

12. Observe que podemos convertir masa en peso simplemente multiplicando por la fuerza debida a la gravedad.

13. Observe que dada una altitud y un ajuste de empuje, la aeronave teóricamente puede volar a dos velocidades diferentes, mientras que esas velocidades se encuentran entre la velocidad mínima (pérdida) y una velocidad máxima (típicamente cerca de la velocidad de divergencia).

14. Se refiere a un valor entre 0 y 1 asociado a la posición del nivel del acelerador.