6.4: Irradiación de Alimentos

Rosana G. Moreira

Departamento de Ingeniería Biológica y Agropecuaria

Universidad A&M de Texas

College Station, Texas, Estados Unidos

Términos Clave

Fuentes de radiación	Distribución de la dosis en profundidad	Aplicaciones de inocuidad alimentaria
Dosis absorbida	Efecto de radiación ionizante	Cinética de inactivación de patógenos

Variables

• λ = longitud de onda
• η = eficiencia de rendimiento
• ρ = densidad del material irradiado
• A _c = área de la sección transversal del alimento o paquete
• A _d = densidad aérea
• c = velocidad de la luz en vacío (3.0 × 10 ⁸ m/s)
• C = tasa de pérdida de energía para el tratamiento con haz de electrones en agua y problemas similares al agua (2.33 MeV/cm)
• dE = energía en volumen infinitesimal dv
• dm = masa en volumen infinitesimal dv
• dm/dt = rendimiento o cantidad de producto por tiempo
• d _p = profundidad de penetración de la energía de radiación por unidad de área
• d = espesor (o profundidad) de los alimentos
• d _opt = profundidad a la que se produce la máxima eficiencia de rendimiento para la irradiación unilateral
• D = dosis o energía aplicada o absorbida por unidad de masa
• D ₁₀ = valor D de radiación o kGy requerido para inactivar el 90% de la población microbiana
• D _max = dosis máxima
• D _min = dosis mínima
• D _sf = dosis de superficie frontal, definida como la dosis administrada a una profundidad d en el alimento, la dosis objetivo
• DUR = relación de uniformidad de dosis
• E = energía máxima absorbida
• E ₅₀ = E _media = energía absorbida a una profundidad de r ₅₀
• E _ab = energía depositada por electrón incidente
• E _p = energía de un fotón
• f = frecuencia de radiación
• h = Constante de Planck (6.626 × 10 ⁻³⁴ J∙s)
• I _a = corriente promedio
• \(I^{“}_{a}\)= densidad de corriente
• k = constante de tasa exponencial
• m = masa de comida
• N = población microbiana a una dosis particular
• N ₀ = población microbiana inicial
• P = potencia de la máquina
• r _max = profundidad a la que se produce la dosis máxima
• r _opt = profundidad a la que la dosis es igual a la dosis de entrada
• r ₃₃ = profundidad a la que la dosis equivale a un tercio de la dosis máxima
• r ₅₀ = profundidad a la que la dosis equivale a la mitad de la dosis máxima
• t = tiempo de irradiación
• v = velocidad
• w = ancho de escaneo

Introducción

La irradiación de alimentos es una tecnología no térmica a menudo llamada “pasteurización en frío” o “pasteurización por irradiación” porque no aumenta la temperatura de los alimentos durante el tratamiento (Cleland, 2005). El proceso se logra mediante el tratamiento de productos alimenticios con radiación ionizante. Otras tecnologías comunes de procesamiento no térmico incluyen alta presión hidrostática, campos eléctricos pulsados de alta intensidad, luz ultravioleta (UV) y plasma frío.

La tecnología de irradiación ha estado en uso por más de 70 años. Ofrece varios beneficios potenciales, incluyendo la inactivación de bacterias comunes transmitidas por los alimentos y la inhibición de procesos enzimáticos (como los que causan brotación y maduración); destrucción de insectos y parásitos; esterilización de especias y hierbas; y extensión de la vida útil. El tratamiento de irradiación no introduce ningún cambio toxicológico, microbiológico, sensorial o nutricional en los productos alimenticios (envasados y sin envasar) más allá de los provocados por las técnicas convencionales de procesamiento de alimentos como el calentamiento (degradación de vitaminas) y la congelación (degradación de la textura) (Morehouse y Komolprasert, 2004). Es la única tecnología de descontaminación disponible comercialmente para tratar frutas y verduras frescas y recién cortadas, que no se someten a tratamientos térmicos como pasteurización o esterilización. Esto es crítico porque muchos brotes recientes de enfermedades transmitidas por alimentos y retiros de productos se han asociado con productos frescos debido a la contaminación con Listeria, Salmonella y Escherichia coli. Aproximadamente 76 millones de enfermedades, 325,000 hospitalizaciones y 5000 muertes ocurren en Estados Unidos anualmente y 1.6 millones de enfermedades, 4000 hospitalizaciones y 105 muertes en Canadá (Health Canada, 2016). Durante 2018, estos brotes causaron 25 mil 606 infecciones, 5 mil 893 hospitalizaciones y 120 muertes en EU (CDC, 2018).

La irradiación de alimentos ha sido aprobada por la Organización Mundial de la Salud (OMS) y la Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO). Al menos 50 países utilizan esta tecnología hoy en día para el tratamiento de más de 60 productos, siendo las especias y condimentos la mayor aplicación. En 2004, Australia se convirtió en el primer país en utilizar la irradiación con fines fitosanitarios, es decir, el tratamiento de plantas para controlar plagas y enfermedades de las plantas con fines de exportación (OIEA, 2015; Eustice, 2017). Alrededor de diez países han establecido acuerdos bilaterales con Estados Unidos para el comercio de frutas y verduras frescas irradiadas. Más de 18,000 toneladas de productos agrícolas son irradiadas para este propósito en todo el mundo. Estados Unidos tiene un fuerte programa comercial de irradiación de alimentos, con aproximadamente 120,000 toneladas de alimentos irradiados anualmente. México, Brasil y Canadá también son grandes productores de productos irradiados. China es el mayor productor de alimentos irradiados en Asia, con más de 200,000 toneladas de alimentos irradiados en 2010 (Eustice, 2017) seguido de India, Tailandia, Pakistán, Malasia, Filipinas y Corea del Sur. Egipto y Sudáfrica utilizan tecnología de irradiación para tratar especias y alimentos secos. Rusia, Costa Rica y Uruguay han obtenido la aprobación para el tratamiento de irradiación de alimentos. Once países de la Unión Europea utilizan irradiación de alimentos pero el resto se han mostrado reacios a adoptar la tecnología debido a los conceptos erróneos de los consumidores, como pensar que los alimentos irradiados son radiactivos con ADN dañado o “sucios” (Maherani et al., 2016).

La irradiación de alimentos se puede lograr usando diferentes fuentes de radiación, como rayos gamma, rayos X y haces de electrones. Si bien los principios básicos de ingeniería se aplican a todas las diferentes fuentes de energía de radiación, este capítulo se centra en los haces de electrones y rayos X de alta energía para demostrar los conceptos porque son una tecnología más aceptable desde el punto de vista ambiental que la tecnología basada en cobalto-60 (rayos gamma).

Resultados

Después de leer este capítulo, deberías poder:

• • Explicar la interacción de la radiación ionizante con los productos alimenticios
• • Cuantificar el efecto de la radiación ionizante sobre los microorganismos y determinar la dosis requerida para inactivar patógenos en los alimentos
• • Seleccionar el mejor enfoque de irradiación para diferentes características de productos alimenticios

Conceptos

La irradiación de alimentos implica el uso de cantidades controladas de radiación ionizante con suficiente energía para ionizar los átomos o moléculas en los alimentos para cumplir con el objetivo de procesamiento deseado. La radiación es la emisión de energía que existe en forma de ondas o fotones a medida que viaja por el espacio o el material alimenticio (energía electromagnética). En otras palabras, se trata de un modo de transferencia de energía. El equivalente de transferencia de calor sería la energía emitida por el Sol.

El tipo de radiación utilizada en el procesamiento de alimentos se limita a rayos gamma de alta energía, rayos X y electrones acelerados o haces de electrones (haces de electrones). Los rayos gamma y los rayos X forman parte del espectro electromagnético (como ondas de radio, microondas, ultravioleta y rayos de luz visible), que se producen en la longitud de onda corta (10 ⁻⁸ a 10 ⁻¹⁵ m), frecuencia más alta (10 ¹⁶ a 10 ²³ Hz), alta energía (10 ² a 10 ⁹ eV) región del espectro. Los electrones de alta energía producidos por los aceleradores de electrones en forma de haces electrónicos pueden tener hasta 10 MeV (megaelectronvoltios = eV × 10 ⁶) de energía (Browne, 2013).

La longitud de onda, o distancia entre picos, λ, de la energía de radiación se define como la relación de la velocidad de la luz en un vacío, c, a la frecuencia, f, de la siguiente manera:

\[ \lambda = \frac{c}{f} \]

donde λ = longitud de onda (m)

c = 3.0 × 10 ⁸ (m/s)

f = frecuencia de radiación (1/s)

Desde una perspectiva cuántico-mecánica, la radiación electromagnética puede considerarse compuesta por fotones (grupos o paquetes de energía que se cuantifican). Por lo tanto, cada fotón tiene un valor específico de energía, E, que puede calcularse de la siguiente manera:

\[ E_{p}=hf \]

donde E _p = energía de un fotón (J)

h = Constante de Planck (6.626 × 10 ⁻³⁴ J·s)

f = frecuencia de radiación (1/s)

La frecuencia, energía y longitud de onda de los diferentes tipos de radiación electromagnética, calculadas mediante las Ecuaciones 6.4.1 y 6.4.2, se dan en la Tabla 6.4.1. Cuanto mayor sea la frecuencia de la onda electromagnética, mayor será la energía y más corta es la longitud de onda. El Cuadro 6.4.1 ilustra que los rayos X y los rayos gamma se utilizan en los procesos de irradiación de alimentos debido a su alta energía. El Cuadro 6.4.1 también explica por qué la exposición a la luz UV solo causaría quemaduras solares (radiación electromagnética de menor energía) mientras que la exposición a rayos X podría ser letal (radiación electromagnética de alta energía).

Cuadro\(\PageIndex{1}\): Frecuencia, nivel de energía y longitud de onda de los diferentes tipos de radiación electromagnética calculados mediante las Ecuaciones 6.4.1 y 6.4.2.

Tipo de Radiación Electromagnética	Frecuencia, f (Hz)	Energía, E (eV)	Longitud de onda, λ (cm)
Rayos gamma	1020	4.140 × 10 ^5	3.0 × 10 ^−10
Rayos X	1018	4.140 × 10 ^2	3.0 × 10 ^−8
Luz UV	1016	4.140	3.0 × 10 ^−6
Luz infrarroja	1014	0.414	3.0 × 10 ^−4

Fuentes de radiación y sus interacciones con la materia

60Co) la más utilizada en aplicaciones de procesamiento de alimentos. Las máquinas de rayos X con una energía máxima de 7.5 MeV y los aceleradores de electrones con una energía máxima de 10 MeV son aprobados por la OMS a nivel mundial porque la energía de estas fuentes de radiación es demasiado baja para inducir radiactividad en el producto alimenticio (Attix, 1986). De igual manera, aunque los rayos gamma son fuentes de radiación de alta energía, las dosis aprobadas para la irradiación de alimentos no inducen ninguna radiactividad en los productos.

Cuadro\(\PageIndex{2}\): Diferentes tipos de fuentes de radiación y sus características (Attix, 1986; Lagunas-Solar, 1995; Miller, 2005). Características Fuente Rayos E Rayos X Cobalto-60
(rayos gamma)

Energía (MeV)

10

5 o 7.5

1.17 y 1.33

Profundidad de penetración (cm)

< 10

100

70

Irradiación bajo demanda (la máquina se puede apagar)

si

si

no

Eficiencia relativa del rendimiento

alto

mediano

bajo

Relación de uniformidad de dosis (D _máx./D _min)

bajo

alto

mediano

Proceso de administración

autorización requerida ^[a]

autorización requerida ^[a]

autorización requerida ^[b]

Tiempo de tratamiento

segundos

minutos

horas

Tasa media de dosis (KGy/s)

~3

0.00001

0.000061

Aplicaciones

Los productos de baja densidad se pueden tratar en cajas

Los productos de densidad baja/media se pueden tratar en cajas de cartón o pellets

Los productos de densidad baja/media se pueden tratar en cajas de cartón o pellets

[a] Se requiere registro estándar

[b] Proceso complejo y difícil con una amplia formación

La diferencia en la naturaleza de los tipos de radiación ionizante da como resultado diferentes capacidades para penetrar la materia (Cuadro 6.4.2). Los rayos gamma y la radiación de rayos X pueden penetrar distancias de un metro o más en el producto, dependiendo de la densidad del producto, mientras que los haces de electrones (haces de electrones), incluso con energía de hasta 10 MeV, pueden penetrar solo varios centímetros. Los aceleradores de haz E oscilan entre 1.35 MeV y 10 MeV (Miller, 2005). Todos los tipos de radiación se vuelven menos intensos cuanto más lejos está la distancia del material radiactivo, a medida que las partículas o los rayos se dispersan más (USNRC, 2018).

Dosis Absorbida

 

La unidad SI de dosis absorbida es el gris (Gy), donde 1 Gy es equivalente a la absorción de 1 J por kg de material. Por lo tanto, la dosis absorbida en cualquier punto del alimento objetivo se expresa como la energía media, dE, impartida por radiación ionizante a la materia en un volumen infinitesimal, dv, en ese punto dividido por la masa infinitesimal, m, de dv:

Cuadro\(\PageIndex{3}\): Requerimiento de dosis absorbida para diferentes tratamientos alimentarios (OIEA, 2002). Tratamiento Dosis Absorbida (kGy) [a]

Inhibición de brotes

0.1—0.2

Desinfestación de insectos

0.3—0.5

Control de parásitos

0.3—0.5

Retraso de maduración

0.5—1

Control de hongos

0.5—3

Inactivación de patógenos

0.5—3

Pasteurización de especias

10—30

Esterilización (inactivación de patógenos)

15—30

[a] 1 kGy = 10 ³ Gy

\[ D=\frac{dE}{dm} \]

donde D = dosis (Gy)

dE = energía en volumen infinitesimal dv (J)

dm = masa en volumen infinitesimal dv (kg)

D representa la energía por unidad de masa que permanece en el material objetivo en un punto determinado para causar cualquier efecto debido a la energía de radiación (Attix, 1986).

En 1928, el roentgen fue concebido como una unidad de exposición, para caracterizar la radiación incidente sobre un material absorbente sin tener en cuenta el carácter del absorbedor. Se definió como la cantidad de radiación que produce una unidad electrostática de iones, ya sea positiva o negativa, por centímetro cúbico de aire a temperatura y presión estándar (STP). En unidades modernas, 1 roentgen equivale a 2.58 × 10 ⁻⁴ culombios/kg de aire (Attix, 1986). En 1953, la Comisión Internacional de Unidades y Medidas de Radiación (ICRU) recomendó el “rad” como una nueva unidad con 1 Gy igual a 100 rad. El término “rad” significa “dosis absorbida por radiación”. Los requerimientos de dosis absorbida para diversos tratamientos que involucran productos alimenticios varían de 0.1 kGy a 30 kGy (Cuadro 6.4.3). El Cuadro 6.4.4 muestra la dosis máxima permisible para diferentes productos en Estados Unidos y en todo el mundo.

Cuadro\(\PageIndex{4}\): Dosis máxima permisible para diferentes alimentos en Estados Unidos y en el mundo (OMS, 1981; ICGFI, 1999; Miller, 2005).

Propósito	Dosis Máxima (kGy)	Producto
Desinfestación	1.0	cualquier alimento
Inhibición de brotes	0.1—0.2	cebollas, papas, ajo
Desinfestación de insectos	0.3—0.5	frutos secos frescos, cereales y legumbres, pescado y carne secos
Control de parásitos	0.3—0.5	carne de cerdo fresca
Retraso de maduración	0.5—1.0	frutas y verduras
Inactivación de patógenos	3.0	aves de corral, huevos con cáscara
Inactivación de patógenos	1.0	frutas y verduras frescas
Inactivación de patógenos	4.5—7.0	carne de res y cerdo frescas y congeladas
Inactivación de patógenos	1.0—3.0	mariscos frescos y congelados
Extensión de vida útil	1.0—3.0	frutas, champiñones, hojas verdes
Pasteurización	10—30	especias
Esterilización comercial	30—50	carne, aves, mariscos, alimentos preparados, alimentos hospitalarios, alimentos para mascotas

La tasa de dosis, o cantidad de energía emitida por unidad de tiempo (dD/dt o\(\frac{d}{dt}(\frac{dE}{dm})\)), determina los tiempos de procesamiento y, por lo tanto, el rendimiento del irradiador (es decir, la cantidad de productos tratados por unidad de tiempo). En esos términos, los electrones de 10 MeV pueden producir un mayor rendimiento (mayor tasa de dosis) en comparación con los rayos X y los rayos gamma (Cuadro 6.4.2). Similar a la dosis absorbida, las tasas de dosis son valores promedio.

Distribución de dosis en profundidad y energía de electrones

El perfil de deposición de energía para un haz de electrones de 10 MeV incidente sobre la superficie de un absorbedor de agua tiene una forma característica (Figura 6.4.1). El eje y es la energía depositada por electrón incidente por unidad de área, E, también descrita como E _ab. Este parámetro es proporcional a la dosis absorbida, D. El eje x es la profundidad de penetración (también llamada espesor de masa), d, en unidades de densidad de área, g/cm ², que es el espesor en cm multiplicado por la densidad volumétrica en g/cm ³:

Figura\(\PageIndex{1}\): Perfil de deposición de energía para electrones de 10 MeV en un absorbedor de agua (adaptado de Miller, 2005).

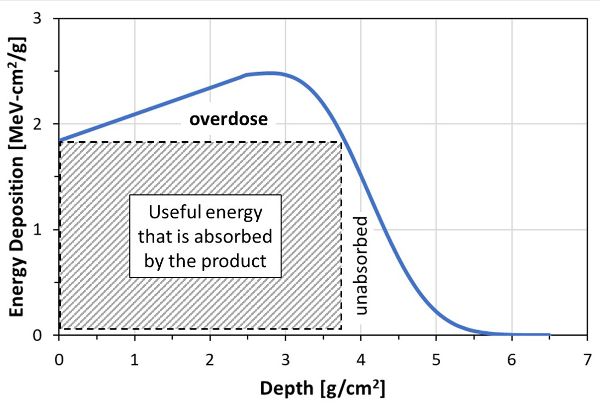
\[ d_{p} = d\rho \]

donde d _p = profundidad de penetración de la energía de radiación por unidad de área (g/cm ²)

d = espesor del material irradiado (cm)

ρ = densidad del material irradiado (g/cm ³)

La profundidad de penetración, d, de la radiación ionizante se define como la profundidad a la que la extrapolación de la cola de la curva dosis-profundidad se encuentra con el eje x (aproximadamente 6 g/cm ² en la Figura 6.4.1). La Figura 6.4.1 también muestra cómo la dosis, D, tiende a aumentar al aumentar la profundidad dentro del producto hasta aproximadamente el punto medio del rango de penetración de electrones y luego cae rápidamente a dosis bajas.

Debido a que la deposición de energía electrónica no es constante, hay una ubicación en el producto que recibirá una dosis mínima, D _min, y otra posición que recibirá la dosis máxima, D _máx. Un parámetro útil para los diseñadores e ingenieros de irradiadores es la relación de uniformidad de dosis (DUR), definida como la relación de dosis máxima a mínima absorbida:

\[ DUR = \frac{D_{max}}{D_{min}} \]

Un DUR cercano a 1.0 representa una distribución uniforme de la dosis en la muestra (Miller, 2005; Moreira et al., 2012). Sin embargo, valores mayores a 1.0 son comunes en aplicaciones comerciales y muchos productos alimenticios pueden tolerar una DUR mayor, de 2 o incluso 3 (OIEA, 2002).

La dosis absorbida, D, a una profundidad particular, d, puede calcularse como el producto de la energía depositada multiplicada por la densidad de corriente por el tiempo de irradiación (Miller, 2005):

\[ D(d) = E_{ab}I^{“}_{A}t \]

donde D = dosis (MeV/g) (1 Gy = 6.24 × 10 ¹² MeV/kg)

E _ab = energía depositada por electrón incidente (MeV-cm ² /g)

\(I^{“}_{A}\)= densidad de corriente (A/cm ²)

t = tiempo (s) de irradiación

Para un producto con espesor, x, la energía representada por el área discontinua en la Figura 6.4.1 es la energía útil absorbida en el producto. La máxima eficiencia ocurrirá cuando la profundidad del producto sea tal que la superficie posterior del producto objetivo reciba la misma dosis que la superficie superior. Por ejemplo, usando la Figura 6.4.1 y asumiendo solo penetración de energía a través del espesor del material, el objetivo con una dosis mínima de 1.85 MeV/g (dosis de entrada) y la profundidad óptima de 3.8 g/cm ² representa una energía absorbida efectiva de aproximadamente 7 MeV (= 1.85 × 3.8). Por lo tanto, utilizando haces electrónicos de 10 MeV, la eficiencia máxima de utilización es del 70% (Miller, 2005).

La profundidad en g/cm ² a la que se produce la máxima eficiencia de rendimiento para la irradiación unilateral se puede calcular como (Miller, 2005):

\[ \text{Depth}_{\text{optimum}}=d_{opt}=0.4\times E - 0.2 \]

donde E es la energía máxima absorbida (MeV).

La ecuación 6.4.7 proporciona una medida útil de la potencia de penetración de electrones del irradiador. La penetración de haces electrónicos de alta energía en materiales irradiados aumenta linealmente con la energía incidente. El rango de electrones (penetración) también depende de la composición atómica del material irradiado. Los materiales con mayores contenidos de electrones (electrones por unidad de masa) tendrán mayores dosis absorbidas cerca de la superficie de entrada, pero menores rangos de electrones (penetración). Por ejemplo, debido a su falta de neutrones, el hidrógeno tiene el doble de electrones atómicos por unidad de masa que cualquier otro elemento. Esto significa que los materiales con mayores contenidos de hidrógeno, como el agua (H ₂ O) y muchos productos alimenticios, tendrán dosis superficiales más altas y menor penetración de electrones que otros materiales (Becker et al., 1979).

En general, las curvas de profundidad dosis-penetración, como la representada por la Figura 6.4.1, muestran un incremento (acumulación) inicialmente marcado de la deposición de energía cerca de la superficie del producto irradiado. Esta región de acumulación es un fenómeno que ocurre en materiales de bajo número atómico debido a la progresiva cascada de electrones secundarios por pérdidas de energía por colisión (OIEA, 2002). A esto le sigue una disminución exponencial de la dosis a mayores profundidades. El valor aproximado de la profundidad de acumulación para los rayos gamma (1.25 MeV) es de 0.5 cm de agua, mientras que la profundidad para haces electrónicos de 10 MeV es de 10.0 cm de agua (OIEA, 2002).

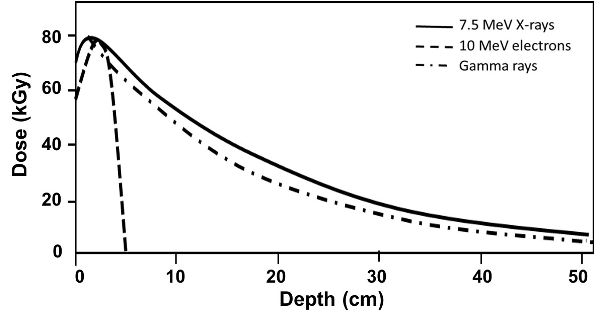
La Figura 6.4.2 muestra el punto de dosis máxima (en kGy) y la absorción de energía tanto para electrones como para fotones (rayos X y rayos gamma). La profundidad de penetración de los haces electrónicos de 10 MeV es limitada ya que depositan su energía en una profundidad corta, con un máximo ubicado después del punto de entrada. En el caso de los rayos gamma, la energía se deposita a mayor distancia, lo que da como resultado una distribución uniforme de la dosis dentro del producto tratado. Las capacidades de penetración tanto de los rayos X de 7.5 MeV como de los rayos gamma son comparables, pero la mayor energía de los rayos X da como resultado una distribución ligeramente más uniforme de las dosis dentro del producto tratado. La configuración del producto influye fuertemente en la distribución de dosis dentro del producto (OIEA, 2002).

Figura\(\PageIndex{2}\): Penetración dosis-profundidad para diferentes fuentes de radiación (rayos X, haces de electrones y rayos gamma) (adaptado del OIEA, 2015).

Figura\(\PageIndex{3}\): Curvas típicas de profundidad-dosis para electrones de diversas energías en el rango aplicable a las operaciones de procesamiento de alimentos (adaptadas del OIEA, 2002). Aquí la profundidad es profundidad de penetración por unidad de área, d _p.

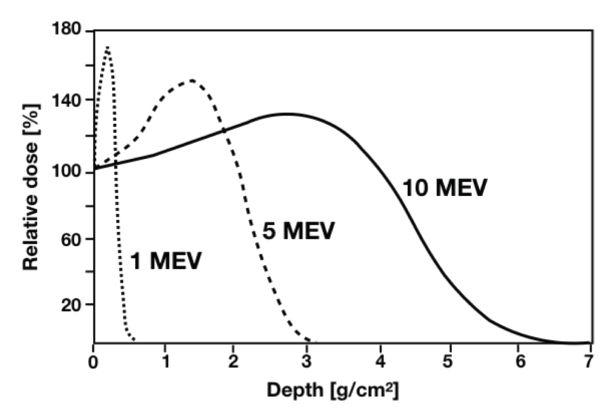
La Figura 6.4.3 muestra las distribuciones de dosis en profundidad en productos equivalentes de agua (como frutas y verduras) que varían de 1 a 10 MeV en términos de dosis relativa en porcentaje. Por ejemplo, para la curva de 10 MeV, si la dosis de entrada (en la superficie) de 1 kGy es del 100%, la dosis relativa a una profundidad de 1 cm ² /g es aproximadamente 110% de la dosis de entrada o 1.1 kGy, y es 0 y 1.40 kGy para los sistemas de irradiación de 1 MeV y 5 MeV, respectivamente.

Las formas de las curvas de profundidad-dosis mostradas en la Figura 6.4.3 pueden definirse mejor en términos de la profundidad de penetración dentro del producto (o grosor del producto) (Figura 6.4.4). Los parámetros definidos en la Figura 6.4.4, r _max, r _opt, r ₅₀ y r ₃₃, son útiles para determinar el grosor máximo del producto que puede irradiarse usando un tipo particular de haz de electrones (1, 5 o 10 MeV). Adicionalmente, la energía depositada se puede determinar a una profundidad específica. Por ejemplo, E ₅₀ a una profundidad de r ₅₀ = 4.53 cm en agua para un sistema de irradiación de 10 MeV es,

\[ E_{mean}=E_{50}=Cr_{50} =2.33(4.53cm)=10.55 MeV \]

donde C es la tasa de pérdida de energía para el tratamiento con haz de electrones en agua y tejidos similares al agua = 2.33 MeV/cm (Strydom et al., 2005).

De la Figura 6.4.4 con r _max igual a 2.8 cm, la dosis máxima es 130% o 1.3 kGy, y la dosis de entrada es igual a la dosis de salida a r _opt igual a 4 cm. Este resultado significa que si el producto irradiado tiene un espesor entre 2.8 y 4 cm, el DUR es constante con un valor de 1.3 (DUR = 1.3 kGy/1.0 kGy). Tal valor de DUR sugiere que el proceso de irradiación proporciona una buena uniformidad en la dosis distribuida a lo largo del grosor del producto. Si el proceso produce una DUR de 2 con una dosis mínima de 0.67 kGy (DUR = 1.35 kGy/0.67 kGy), el espesor útil máximo del producto irradiado será 4.5 cm o r ₅₀, profundidad a la que la dosis es la mitad de la dosis máxima.

Figura\(\PageIndex{4}\): Curva de profundidad-dosis para electrones de 10 MeV en agua, donde la dosis de entrada (superficie) es del 100% (adaptada del OIEA, 2002). r _max es la profundidad en cm a la que se produce la dosis máxima, r _opt es la profundidad a la que la dosis es igual a la dosis de entrada (también descrita por la Ecuación 6.4.7), r ₅₀ es la profundidad a la que la dosis equivale a la mitad de la dosis máxima, y r ₃₃ es la profundidad a la que la dosis equivale a un tercio de la dosis máxima.

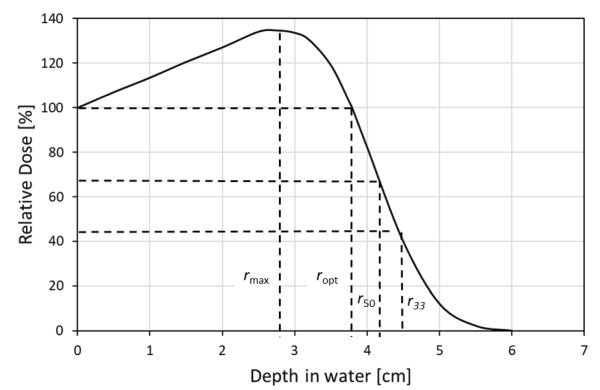
Tenga en cuenta que r ₅₀ > r _opt. De ahí que si el grosor del producto excede r _opt, el DUR aumenta. A medida que el DUR se acerca al infinito a una profundidad de 6.5 cm para un haz de electrones de 10 MeV (Figura 6.4.4), cualquier parte del producto más allá de esa profundidad permanecerá sin exponer al tratamiento de irradiación. Por lo tanto, el grosor máximo del producto procesable para este sistema de irradiación será de 6.5 cm. Este resultado resalta un problema crítico cuando se utilizan aceleradores de haz de electrones para pasteurizar o esterilizar productos alimenticios, que necesitan ser expuestos en su totalidad a la energía de radiación.

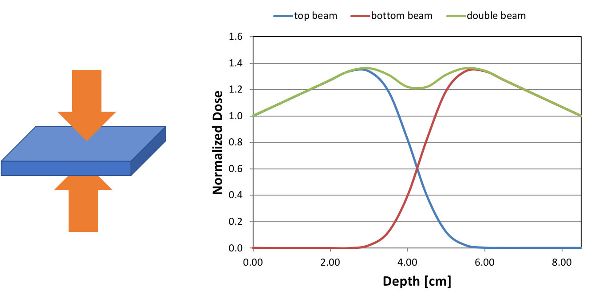
El ingeniero tiene la opción de aplicar las vigas eléctricas utilizando la configuración de haz de electrones único (que expone el alimento objetivo solo en la superficie superior o inferior) o la configuración de doble haz (que expone el alimento objetivo tanto en la superficie superior como en la inferior). La Figura 6.4.5 ilustra la diferencia entre los sistemas de irradiación unilateral y bilateral que utilizan electrones de 10 MeV en agua cuando DUR es 1.35.

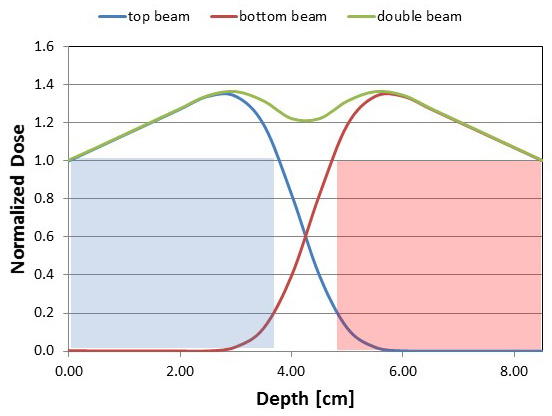
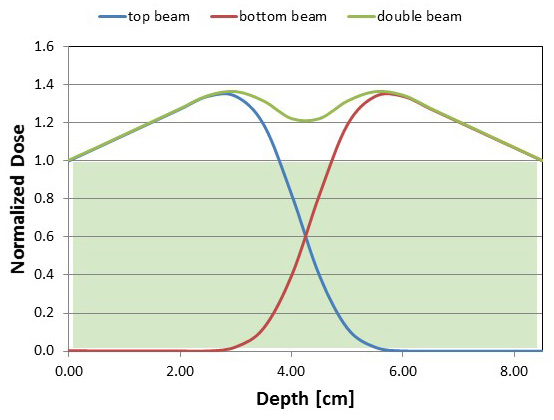
La Figura 6.4.5 muestra que al irradiar solo desde arriba o abajo, el grosor procesable máximo será cercano a 4 cm (áreas sombreadas, Figura 6.4.6), mientras que el sistema de doble haz aumenta el grosor procesable máximo a aproximadamente 8.3 cm (área sombreada, Figura 6.4.7). Por lo tanto, para mejorar la capacidad de penetración de un tratamiento de haz de electrones de 10 MeV, dos aceleradores de 10 MeV, uno irradiando desde la parte superior y el otro desde la parte inferior de un sistema transportador, se utilizan frecuentemente en aplicaciones comerciales (OIEA, 2002).

Figura\(\PageIndex{5}\): Distribuciones de dosis de profundidad para electrones de 10 MeV en agua para configuraciones de un lado y de doble cara y DUR = 1.35. La dosis normalizada es la relación entre la dosis máxima y la dosis de entrada (Miller, 2005).

La profundidad a la que se produce la máxima eficiencia de rendimiento para la irradiación de doble cara se puede calcular como (Miller, 2005):

\[ Depth_{optimum} = d_{opt} = 0.9\times E-0.4 \]

Medición de la dosis absorbida

La efectividad de la radiación ionizante en aplicaciones de procesamiento de alimentos depende de la correcta entrega de la dosis absorbida. Para diseñar el proceso correcto de irradiación de alimentos, el operador debe ser capaz de (1) medir la dosis absorbida entregada al producto alimenticio utilizando métodos de dosimetría confiables; (2) determinar los patrones de distribución de dosis en el paquete del producto; y (3) controlar el proceso de radiación de rutina (a través del control del proceso procedimientos). Los dosímetros se utilizan para el control de calidad y procesos en investigación de radiación y procesamiento comercial.

Las técnicas confiables para medir la dosis, llamadas dosimetría, son cruciales para garantizar la integridad del proceso de irradiación. Dosimetría incorrecta puede resultar en un proceso ineficaz de irradiación de alimentos. Los sistemas de dosimetría incluyen dosímetros físicos o químicos e instrumentación de medición, tales como espectrofotómetros y espectrómetros de resonancia paramagnética electrónica (EPR). Un dosímetro es un dispositivo capaz de proporcionar una lectura que es una medida de la dosis absorbida, D, depositada en su volumen sensible, V, por radiación ionizante. El instrumento de medición debe estar bien caracterizado para que dé resultados reproducibles y precisos (Attix, 1986).

Figura\(\PageIndex{6}\): Grosor máximo de penetración para configuraciones de haz de electrones solo superior e inferior utilizando electrones de 10 MeV en agua y DUR = 1.35.

Existen cuatro categorías de sistemas de dosimetría según su precisión intrínseca y uso (OIEA, 2002):

• • Los estándares primarios (cámara de iones, calorímetros) miden la dosis absorbida absoluta (es decir, no necesita ser calibrada) en unidades SI.

Figura\(\PageIndex{7}\): Grosor máximo de penetración para irradiación de haz de electrones de doble cara usando electrones de 10 MeV en agua (DUR = 1.35).

• • Los estándares de referencia (alanina, Fricke y otros químicos) tienen una alta calidad metrológica que se puede utilizar como estándar de referencia para calibrar otros dosímetros. Deben ser calibrados contra un estándar primario, generalmente mediante el uso de un dosímetro estándar de transferencia.
• • Los estándares de transferencia (dosímetro termoluminiscente, TLD) se utilizan para transferir información de dosis de un laboratorio nacional de estándares a una instalación de irradiación para establecer la trazabilidad a ese laboratorio de estándares. Deben ser utilizados en las condiciones especificadas por el laboratorio emisor. Necesitan ser calibrados.
• • Los dosímetros de rutina (monitoreo de procesos, películas radiocrómicas) se utilizan en instalaciones de procesamiento de radiación para mapeo de dosis y para monitoreo de procesos para control de calidad. Deben ser calibrados frecuentemente contra dosímetros de referencia o transferencia.

Irradiación de alimentos y aplicaciones de inocuidad alimentaria

Los principales microorganismos patógenos de preocupación en el procesamiento de alimentos son Salmonella spp., Escherichia coli y Listeria spp. La abreviatura “spp.” significa más de una especie en ese género, aquí significa que hay varios tipos de bacterias en el mismo grupo.

Efecto de la Radiación Ionizante sobre Patógenos

La inactivación de patógenos es el efecto final de la irradiación de los alimentos. La exposición a la radiación ionizante tiene dos efectos principales sobre los microorganismos patógenos. Primero, la energía de radiación puede romper directamente hebras (simples o dobles) del ADN del microorganismo. El segundo efecto ocurre indirectamente cuando la energía provoca la radiólisis del agua para formar radicales hidrógeno (H+) e hidroxilo (^• OH) muy reactivos. Estos radicales pueden recombinarse para producir aún más radicales reactivos como el superóxido (HO ₂), el peróxido (H _{2 O 2}) y el ozono (O ₃), los cuales tienen un papel importante en la inactivación de patógenos en los alimentos. Aunque el ADN es el objetivo principal, otras moléculas bioactivas, como las enzimas, también pueden sufrir inactivación debido al daño por radiación, lo que potencia la eficacia del tratamiento de irradiación.

Cinética de la inactivación de patógenos

El enfoque tradicional utilizado en los cálculos de procesamiento térmico es desarrollar curvas de supervivencia, que son parcelas semi-logarítmicas de poblaciones de microorganismos en función del tiempo a una temperatura de proceso dada. Este mismo enfoque se puede utilizar para desarrollar curvas de supervivencia a la radiación, es decir, gráficas del log del cambio en poblaciones microbianas en función de la dosis aplicada. En este capítulo, solo se describen cinéticas de primer orden de destrucción microbiana.

Figura\(\PageIndex{8}\): Curva de supervivencia típica que muestra el comportamiento cinético de primer orden con N ₀ = población microbiana inicial y N = población microbiana a una dosis particular, tanto en UFC/g como UFC/ml. La curva discontinua es la sección inicial no lineal de la curva.

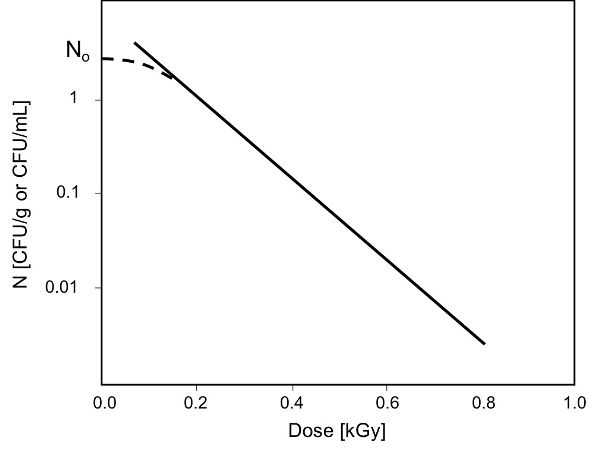
La Figura 6.4.8 es una curva de supervivencia obtenida para la inactivación de un patógeno en un producto alimenticio debido a la exposición a la energía de radiación. Con base en la cinética de primer orden (es decir, ignorando la sección no lineal inicial de la curva indicada por la flecha y la línea discontinua en la Figura 6.4.8), la tasa de inactivación microbiana se describe por:

\[ \frac{dN}{dD}=-kD \]

donde N = población microbiana a una dosis particular (UFC/g o UFC/ml; UFC significa unidades formadoras de colonias)

D = la dosis aplicada (kGy)

k = constante de velocidad exponencial (1/kGy)

La resistencia a la radiación del microorganismo diana generalmente se reporta como el valor D de radiación, D ₁₀, definido como la cantidad de energía de radiación (kGy) requerida para inactivar el 90% (o una reducción logarítmica) del microorganismo específico (Thayer et al., 1990). Usando esta definición e integrando la Ecuación 6.4.10 rinde:

\[ N=N_{0}e^{-kD_{10}} \]

donde N ₀ = población microbiana inicial (UFC/g o UFC/ml)

Con base en la Figura 6.4.8 y la Ecuación 6.4.11, la inversa de la pendiente de la línea es el valor D ₁₀ y es equivalente al valor D utilizado en los cálculos de procesos térmicos excepto que estos tienen unidades de tiempo como la pendiente de cambio poblacional versus tiempo de proceso. La relación entre el valor D ₁₀ y la constante de velocidad es:

\[ k=\frac{1}{D_{10}} \]

El valor D ₁₀ varía según el patógeno objetivo, tipo y condición de los alimentos (enteros, triturados, pelados, cortados, congelados, etc.) y la atmósfera en la que se envasa (por ejemplo, alimentos envasados al vacío, pH, humedad y temperatura) (Niemira, 2007; Olaimat y Holley, 2012; Moreira et al., 2012). Por ejemplo, los valores de D ₁₀ para Salmonella spp. y Listeria spp. en productos frescos pueden oscilar entre 0.16 y 0.54 kGy mientras que Escherichia coli es ligeramente más resistente al tratamiento con irradiación (a veces hasta 1 kGy) (Fan, 2012; Rajtowski et al., 2003). Cuando se irradian los tomates, los valores de D ₁₀ para Escherichia coli O157:H7, Salmonella spp., y Listeria monocytogenes son alrededor de 0.39, 0.56 y 0.66 kGy, respectivamente (Mahmoud et al., 2010). En aplicaciones comerciales, la regla general es diseñar un tratamiento de irradiación para una reducción de cinco log o 5 D ₁₀ en la población del patógeno diana.

Aplicaciones

El objetivo de un proceso de irradiación de alimentos es entregar la dosis mínima efectiva de radiación a todas las porciones del producto. Una dosis demasiado alta (o energía) en cualquier región del producto objetivo podría llevar al desperdicio de energía y al deterioro de la calidad del producto.

Para diseñar un proceso de irradiación de alimentos, se debe especificar la dosis absorbida en el material de interés debido a que diferentes materiales tienen diferentes propiedades de absorción de radiación. En el caso de los productos alimenticios, el material de interés es el agua porque la mayoría de los alimentos se comportan esencialmente como agua independientemente de su contenido de agua. Se deben utilizar los requisitos de dosis y las dosis máximas permitidas para aplicaciones específicas (Cuadros 6.4.3 y 6.4.4).

Las estimaciones de costos para las instalaciones de irradiación de alimentos incluyen el costo de capital del equipo, la instalación y el blindaje, el manejo de materiales y la ingeniería, y costos variables que incluyen electricidad, mantenimiento y mano de obra El costo aproximado de una instalación de acelerador de haz de electrones para una tasa de producción de 2000 horas anuales es de entre 2 y 5 millones de dólares estadounidenses y se ha mantenido bastante estable (Morrison, 1989; Miller, 2005; University of Wisconsin, 2019).

Selección de Tecnología

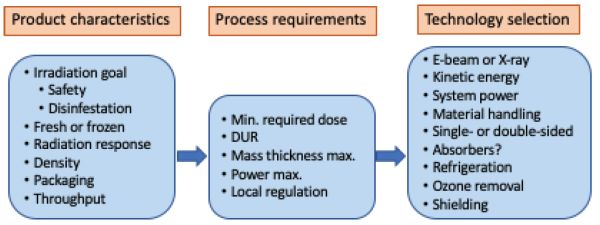
La selección de la tecnología adecuada para una aplicación de irradiación de alimentos en particular depende de muchos factores, incluyendo las características de los productos alimenticios y los requisitos de procesamiento (Miller, 2005). La Figura 6.4.9 muestra los pasos necesarios para elegir un enfoque de irradiación de alimentos.

El primer paso es definir las características del producto. ¿Cuál es el objetivo principal del proceso? ¿Cuál es el estado del producto, es decir, congelado, sin envasar, etc.? ¿Cuál es la densidad, forma y caudal másico del producto pasando por el acelerador? El segundo paso especifica los requisitos del proceso, incluyendo el grosor del producto y la DUR aceptable (Ecuación 6.4.5). El paso final es seleccionar la tecnología de radiación adecuada en función de las características del producto y los requisitos del proceso. La selección incluye determinar la mejor tecnología (haces electrónicos versus rayos X versus rayos gamma), el tamaño del acelerador o aceleradores de rayos X y, en el caso de los haces electrónicos, si el tratamiento de haz simple o doble será más efectivo.

Figura\(\PageIndex{9}\): Pasos necesarios para seleccionar la tecnología de irradiación adecuada para una aplicación de procesamiento de alimentos (adaptada de Miller, 2005).

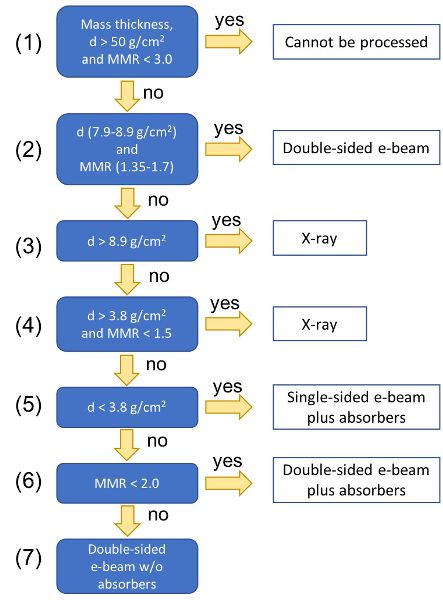
Un diagrama de flujo simplificado proporciona pautas a seguir para seleccionar la tecnología adecuada para la irradiación de alimentos (Figura 6.4.10). El ingeniero primero debe determinar si el producto podría irradiarse efectivamente en función de las relaciones de dosis máxima a mínima y los conceptos de eficiencia energética. La profundidad de penetración depende del grosor de la masa del producto (g/cm ²), que se basa en las dimensiones y densidad del producto y/o paquete (Ecuación 6.4.4). Para los tratamientos de inocuidad alimentaria, el DUR se basa en el requerimiento de dosis mínima para reducir la población de un determinado patógeno (es decir, el valor D ₁₀, Ecuación 6.4.12) y la dosis máxima permitida por la regulación local o la dosis que un producto puede tolerar sin degradar su calidad. Como se indica en la Figura 6.4.10, en general, el producto no será adecuado para el tratamiento de irradiación cuando su espesor de masa sea mayor a 50 g/cm ² y DUR debe ser menor a 3.

Figura\(\PageIndex{10}\): Diagrama de flujo de decisión para seleccionar el enfoque de irradiación correcto (adaptado de Miller, 2005). La MMR es el rango aceptable de proporciones de dosis máxima a mínima (DUR).

Finalmente, el ingeniero deberá seleccionar los sistemas de manejo del producto para transportar el producto alimenticio dentro y fuera de los irradiadores de haz de electrones y rayos X a través de transportadores. La orientación de los irradiadores es una consideración importante ya que los haces de electrones están orientados verticalmente al producto, mientras que los rayos X de mayor penetración permiten la irradiación horizontal de los productos. La tasa de dosis se establece variando la velocidad de los transportadores. El ingeniero también debe determinar si se deben usar absorbentes para reducir la dosis de entrada; proporcionar refrigeración de la instalación, si es necesario, ya que muchos productos alimenticios son perecederos; incluir el blindaje de la instalación (los rayos X requieren paredes más gruesas que el procesamiento de rayos electrónicos), y prever la eliminación de ozono (un sub- producto de irradiación por ionización de oxígeno en el aire) (Miller, 2005). Antes de ingresar al sistema de irradiación, los productos son inspeccionados en áreas de espera donde los productos son paletizados y cargados en contenedores para ser transportados en transportadores a través de los irradiadores. Los productos irradiados se cargan en vehículos de transporte o se almacenan en cámaras refrigeradas para su distribución a minoristas.

La velocidad, v, en cm/s, del transportador que transporta los alimentos a través de una instalación de escaneo de haz de electrones está determinada por (Miller, 2005):

\[ v = \frac{1.85\times10^{6}I_{a}}{wD_{sf}} \]

Figura\(\PageIndex{11}\): Configuración típica de irradiación por haz de electrones que muestra paquetes planos de alimentos colocados sobre el transportador con el haz dirigido hacia abajo y escaneados horizontalmente a través del producto. Para la irradiación de doble haz, un segundo haz se dirige verticalmente hacia arriba (adaptado de Miller, 2005).

donde I _a = corriente promedio (A), un parámetro de configuración del acelerador de haz de electrones

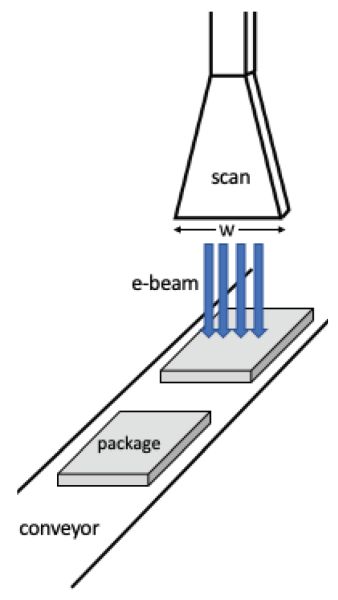
w = ancho de escaneo (cm), un parámetro de configuración del acelerador de haz de electrones (ver Figura 6.4.11)

D _sf = la dosis de superficie frontal (kGy), definida como la dosis administrada a una profundidad d en el alimento (Figura 6.4.11); la dosis objetivo

La velocidad del transportador está directamente relacionada con el rendimiento como:

\[ v = \frac{dm/dt}{A_{d}w} \]

donde dm/dt = rendimiento o cantidad de producto por tiempo (g/s)

A _d = densidad aérea (g/cm ²) obtenida de la Ecuación 6.4.15:

\[ A_{d}=\rho d \]

donde ρ = densidad de alimentos (g/cm ³)

d = espesor (o profundidad) de los alimentos (cm)

Las ecuaciones 6.4.13 y 6.4.14 muestran que para un sistema con corriente promedio fija y ancho de escaneo, cuanto más rápida sea la velocidad del transportador, más producto se procesa en la instalación y menor es la dosis que recibe. Las velocidades típicas del transportador oscilan entre 5 y 10 m/minuto.

La masa total del producto que corre a través de la cinta transportadora se calcula como:

\[ m=A_{d}A_{c} \]

donde m = masa de alimento (kg)

A _d = densidad aérea de la Ecuación 6.4.15

A _c = área transversal del alimento o paquete (m ²)

Los requisitos de rendimiento de las instalaciones de haz de electrones (dm/dt) se estiman con base en la potencia del haz, la dosis mínima requerida y el modo de irradiación (por ejemplo, haz de electrones frente a rayos X) de la siguiente manera (Miller, 2005):

\[ \frac{dm}{dt}=\frac{\eta P}{D} \]

donde η = eficiencia de rendimiento, que es 0.025 a 0.035 a 5 MeV y 0.04 a 0.05 a 7.5 MeV para irradiación de rayos X, y 0.4 a 0.5 para el modo de haz de electrones (Miller, 2005)

P = potencia de la máquina (kW)

D = requerimiento de dosis mínima (kGy), que varía de 250 Gy para la desinfestación a 6—10 kGy para la conservación de la frescura de las especias

Ejemplos

Ejemplo\(\PageIndex{1}\)

Ejemplo 1: Interacción de la radiación ionizante con la materia

Problema:

Si la densidad de corriente incidente en la superficie es de 10 ⁻⁶ A/cm ² del absorbedor de agua en la Figura 6.4.1 y la energía depositada por electrón incidente es de 1.85 MeV-cm ^2/g, determine la dosis absorbida en kGy después de 1 segundo.

Solución

Usando la Ecuación 6.4.6:

\( D(d)=E_{ab}I^{“}_{A}t \)(Ecuación\(\PageIndex{6}\))

\( D(d)=(1.85 MeV \frac{cm^{2}}{g})\times (10^{-6}\frac{A}{cm^{2}})\times 1\ s \)

con 1 MeV = 10 ⁶ eV:

\( D(d)=(1.85 \frac{cm^{2}}{g})\times (10^{-6}\frac{A}{cm^{2}})\times 1\ s \)

En unidades de energía, 1 eV (electrovoltio) equivale a 1.60218 × 10 ⁻¹⁹ Julios y 1 kJ = 1000 J

\( D(d)=(1.85 \frac{cm^{2}}{g})\times (10^{-6}\frac{A}{cm^{2}})\times 1\ s(\frac{1C}{1A\times s})\times(\frac{1.6022\times10^{-19}J}{1\ eV})\times(\frac{1}{1.6022\times10^{-19}C}) \)

Finalmente, la dosis en kGy es:

\( D(d)=1.85\frac{kJ}{kg} \text{ or }kGy \)

La dosis absorbida después de 1 segundo es de 1.85 kGy.

Ejemplo\(\PageIndex{2}\)

Ejemplo 2: Cálculo de la relación de uniformidad de dosis (DUR)

Problema:

La Figura 6.4.1 muestra que la dosis absorbida aumenta a una profundidad de 2.75 g/cm ² dentro del absorbedor de agua irradiada. (a) Encontrar la relación de uniformidad de dosis (DUR). b) Comentar los cambios (si los hubiere) a este parámetro en función de la profundidad en el blanco irradiado.

Solución

1. (a) Con base en la Figura 6.4.1 y usando la Ecuación 6.4.5, calcular el DUR:

DUR = D _máx./D _mín = 2.5/1.85 = 1.35

1. El valor de DUR se encuentra dentro del rango aceptable para la uniformidad de dosis en sistemas irradiadores comerciales (cercano a 1.0).
2. (b) Con base en la Figura 6.4.1, el DUR permanece constante (= 1.35) hasta una profundidad de 3.8 g/cm ². Más allá de esta profundidad, la dosis mínima disminuye lo que aumenta la DUR. Esto se muestra claramente en la Figura 6.4.1 a medida que la dosis aumenta al aumentar la profundidad dentro del producto y luego disminuye.

Ejemplo\(\PageIndex{3}\)

Ejemplo 3: Grosor del producto para irradiación de haz de electrones de una cara

Problema:

Determine el grosor máximo permitido del producto para la irradiación de haz electrónico unilateral con electrones de 10 MeV si es aceptable una relación de uniformidad de dosis de 3.

Solución

De la Figura 6.4.4 y usando la Ecuación 6.4.5, determinar la profundidad en cm para DUR = 3

DUR = D _máx/D _min

D _max = 130% o 1.3 kGy (Figura 6.4.4) y D _min = 1.3/3 = 0.43 kGy o 43% dosis relativa

Nuevamente, a partir de la Figura 6.4.4, el valor de profundidad es de 4.8 cm = r ₃₃.

Así, el grosor máximo permitido del producto será de 4.8 cm y la dosis de salida equivale a un tercio de la dosis máxima.

Ejemplo\(\PageIndex{4}\)

Ejemplo 4: Eficiencia del tratamiento de irradiación de una cara frente a doble cara

Problema:

Determine la profundidad a la máxima eficiencia de rendimiento para la irradiación de agua de 10 MeV de una sola cara y doble cara (5 cm de grosor) cuando la energía absorbida es de (a) 1.50 MeV-cm ² /g, (b) 2.20 MeV-cm ² /g, y (c) 2.40 MeV-cm ² /g.

Solución

Seleccione la ecuación apropiada y calcule la profundidad en cm.

Para irradiación de un solo lado, use la Ecuación 6.4.7:

\( d_{opt}=0.4\times E - 0.2 \)

1. (a) 1.50 MeV-cm ² /g

\( d_{opt}=0.4\times (1.50) - 0.2 = 0.40 \text{ g/cm}^{2} \)

1. (b) 2.22 MeV-cm ² /g

\( d_{opt}=0.4\times (2.22) - 0.2 = 0.68 \text{ g/cm}^{2} \)

1. (c) 2.40 MeV-cm ² /g

\( d_{opt}=0.4\times (2.40) - 0.2 = 0.76 \text{ g/cm}^{2} \)

Para irradiación de doble cara, utilice la Ecuación 6.4.9:

\( d_{opt}=0.9\times E - 0.4 \)

1. (a) 1.50 MeV-cm ² /g

\( d_{opt}=0.9\times (1.50) - 0.4 = 0.95 \text{ g/cm}^{2} \)

1. (b) 2.22 MeV-cm ² /g

\( d_{opt}=0.9\times (2.22) - 0.4 = 1.60 \text{ g/cm}^{2} \)

1. (c) 2.40 MeV-cm ² /g

\( d_{opt}=0.9\times (2.40) - 0.4 = 1.76 \text{ g/cm}^{2} \)

Energía Absorbida (MeV-cm ^2 /g)	d opt (g/cm ^2) de una sola cara	d opt (g/cm ^2) Doble cara
1.50	0.40	0.95
2.22	0.68	1.60
2.40	0.76	1.76

^{Los resultados demuestran que la configuración de doble haz es más efectiva con respecto a la profundidad de penetración con mínima utilización de energía, por ejemplo, penetración de 0.95 g/cm 2 versus 0.40 g/cm 2 usando haces de electrones con 1.5 MeV-cm 2/g de energía.}

Ejemplo\(\PageIndex{5}\)

Ejemplo 5: Interacción de la radiación ionizante con el producto alimenticio y efecto sobre la profundidad de penetración de la dosis

Problema:

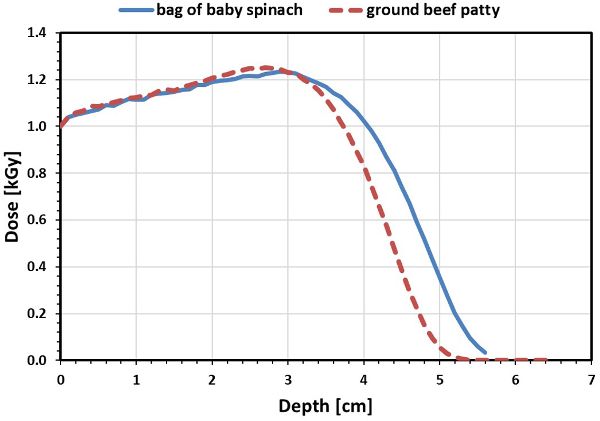
En la Figura 6.4.12 se muestran comparaciones de distribuciones de dosis de profundidad electrónica de 10 MeV en una bolsa de hojas de espinaca bebé envasadas al vacío (grosor de masa = 5.1 g/cm ^{2) y empanada de carne molida (grosor de masa = 5.1 g/cm 2}). Determine la profundidad a la que se produce la dosis máxima para ambos productos alimenticios y comente sus resultados.

Figura\(\PageIndex{12}\): Dosis absorbida vs. profundidad de penetración en hojas de espinaca bebé envasadas al vacío y empanada de carne molida a 10 MeV de energía electrónica incidente.

Solución

Localice la profundidad (eje x) a la que la dosis (eje y) es máxima. Para la espinaca, la profundidad es de 3.00 cm y para la empanada de carne molida, profundidad = 2.70 cm.

Ambos materiales tienen una composición atómica muy similar y, por lo tanto, absorben la energía incidente de manera muy similar.

Ejemplo\(\PageIndex{6}\)

Ejemplo 6: Cálculo del valor de radiación D ₁₀

Problema:

Las hojas de lechuga romana se expusieron a dosis de radiación de hasta 1.0 kGy usando un irradiador de haz electrónico de 10 MeV para inactivar un patógeno. La población de sobrevivientes a cada dosis se midió justo después de la irradiación (ver tabla a continuación).

Número de patógenos (UFC/g) en hojas de lechuga romana en función de la dosis de radiación:

Dosis (kGy)	Población (log UFC/g)
0	6.70
0.25	5.50
0.50	4.30
0.75	3.30
1.00	2.00

1. a) Calcular el valor D ₁₀ del patógeno en el producto fresco y determinar el nivel de dosis requerido para una reducción de 5 log en la población del patógeno. El punto de datos para una dosis de 0 kGy representa el producto no irradiado.
2. b) Si la dosis máxima aprobada para irradiación de hortalizas frescas es cercana a 1 kGy, ¿es adecuado el tratamiento de irradiación?

Solución

Primero, graficar el logaritmo de la población de sobrevivientes en función de la dosis a partir de los datos dados y determinar el valor D ₁₀ a partir de la inversa de la pendiente de la línea (Figura 6.4.13).

^{Figura\(\PageIndex{13}\): Cálculo del valor D ₁₀ asumiendo la inactivación de la radiación como cinética de primer orden.}

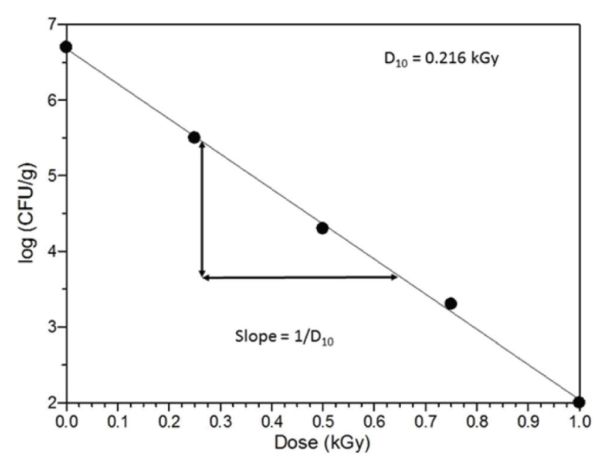
\( Slope = -\frac{logN_{1}-logN_{2}}{D_{1}-D_{2}} =-\frac{5-4}{0.375-0.591}=-\frac{1}{-0.216}=\frac{1}{0.216} \)

Luego, determinar la dosis requerida para una reducción de 5 log en la población microbiana, es decir, 5 D ₁₀, y verificar si 5 D ₁₀ < 1.0 kGy. En caso afirmativo, el proceso es adecuado para el tratamiento de los productos frescos. Si 5 D ₁₀ > 1.0 kGy, se debe considerar otro proceso.

5 D ₁₀ = 5 × 0.216 kGy = 1.10 kGy

Este proceso de irradiación sería adecuado porque la población de patógenos en las hojas de lechuga romana se reducirá en 5 logs cuando se exponga a una dosis de aproximadamente 1.0 kGy utilizando haces de electrones de 10 MeV.

Ejemplo\(\PageIndex{7}\)

Ejemplo 7: Selección de la mejor tecnología de irradiación

Problema:

Un haz de electrones de 10 MeV y un acelerador de rayos X de 5 MeV están disponibles para irradiar los siguientes productos. Seleccione la mejor tecnología de irradiación para tratar cada uno de los productos. Asumir una dosis mínima de 1 kGy.

1. (a) Empanada de carne molida contaminada con Escherichia coli O157:H7, D _max = 1.25 kGy (espesor de masa = 8.5 g/cm ²)
2. (b) Tomate contaminado con Listeria monocytogenes, D _max = 1.4 kGy (espesor de masa = 3.2 g/cm ²)
3. c) Lechuga romana contaminada con Salmonella Poona, D _max = 1.37 kGy (espesor de masa = 4.1 g/cm ²)

Solución

Utilizar la información dada y el diagrama de flujo (Figura 6.4.10) para determinar si se deben utilizar haces electrónicos o rayos X para la irradiación de los diferentes productos.

1. (a) DUR para empanada de carne (usando la Ecuación 6.4.5, DUR = D _máx/D _min) = 1.25 KGy/1 kGy = 1.25 = MMR

   Siguiendo la Figura 6.4.10 con espesor de masa d = 8.5 g/cm ² y MMR = 1.25 conduce a la condición 4: d >3.8 g/cm ² y MMR < 1.5 y selección de rayos X como la tecnología apropiada para la empanada de carne.

2. (b) DUR para muestra de tomate (usando la Ecuación 6.4.5, DUR = D _máx/D _min): 1.4 KGy/1 kGy = 1.4 = MMR

   Siguiendo la Figura 6.4.10 con espesor de masa d = 3.2 g/cm ² y MMR = 1.4 conduce a la condición 6 o 7: d < 3.8 g/cm ² y la selección de haz de electrones simple o doble cara sería apropiada para la muestra de tomate.

3. (c) DUR para lechuga romana (usando la Ecuación 6.4.5, DUR = D _máx/D _min): 1.37 KGy/1 kGy = 1.37 = MMR

Siguiendo la Figura 6.4.10 con espesor de masa d = 4.1 g/cm ² y MMR = 1.37 lleva a la condición 4: Grosor de masa d = 4.1 g/cm ². Desde d > 3.8 g/cm ² y MMR < 1.5, seleccione rayos X como la tecnología apropiada para la lechuga romana.

Producto	Criterios	Elección de la tecnología de radiación
Empanada de carne	d >3.8 g/cm ^2, MMR < 1.5	Rayos X
Tomate	d < 3.8 g/cm ^2, MMR < 1.5	Vigas E
Lechuga romana	d > 3.8 g/cm ^2, MMR < 1.5	Rayos X

Ejemplo\(\PageIndex{8}\)

Ejemplo 8: Calcular la dosis requerida para una reducción de 5 log de la población de patógenos

Problema:

Calcular la dosis requerida para una reducción de 5 log del patógeno para los tres productos del Ejemplo 6.4.7 utilizando la siguiente información. Para cada producto, determine si la dosis requerida es menor que la dosis máxima permitida para ese producto.

1. a) Empanada de carne molida contaminada con Escherichia coli O157:H7 (D ₁₀ = 0.58 kGy)
2. b) Tomate contaminado con Listeria monocytogenes (D ₁₀ = 0.22 kGy)
3. c) Lechuga romana contaminada con Salmonella Poona (D ₁₀ = 0.32 kGy)

Solución

Dado el valor D ₁₀ para cada patógeno, calcular 5D. El patógeno con mayor valor 5D es el más resistente a la irradiación y requerirá tratamiento a dosis más altas.

Producto	Patógeno	5D (kGy)
Empanada de carne molida	Escherichia coli O157:H7	2.90
Tomate	Listeria monocytogenes	1.10
Lechuga romana	Salmonella Poona	1.60

La E. coli en las empanadas de carne requerirá dosis mayores para lograr un nivel de inactivación de 5 log que las dosis requeridas para tratar los dos productos frescos. El tratamiento requerido para las muestras de tomate se encuentra dentro del nivel de dosis aceptable para frutas y verduras (aproximadamente 1 kGy). La Salmonella en la lechuga requerirá una dosis ligeramente mayor pero la Administración de Alimentos y Medicamentos de Estados Unidos (FDA, 2018) permite hasta 4 kGy para el tratamiento de verduras de hoja verde. La dosis máxima permisible para la inactivación de patógenos en carne fresca y congelada oscila entre 4.5—7.0 kGy en diferentes países (Cuadro 6.4.4).

Ejemplo\(\PageIndex{9}\)

Ejemplo 9: Cálculo de la velocidad del transportador en un sistema de viga eléctrica

Problema:

Calcule la velocidad del transportador requerida para una irradiación de dosis de entrada de 1.5 kGy (dosis de superficie frontal) para un proceso de un solo lado usando una viga de 10 MeV, 1 mA con un ancho de escaneo de 120 cm.

Solución

Calcule la velocidad del transportador usando la Ecuación 6.4.13:

\( v=\frac{1.85\times10^{6}I_{a}}{wD_{sf}} \)

_{La velocidad del transportador, v, con los valores dados de D sf = 1.5 kGy, I a = 10 ⁻³ A y w = 120 cm es:}

\( v=\frac{1.85\times10^{6}I_{a}}{wD_{sf}} = \frac{1.85\times10^{6}\times10^{-3}}{120\times1.5} = 10.28 \text{ cm/s} \)

La velocidad del transportador varía según el rendimiento del producto. En este caso, el transportador debe funcionar a 10.28 cm/s (6 m/min) para asegurar una dosis de entrada de 1.5 kGy al tratar los alimentos con un acelerador de haz de electrones de 10 MeV en modo de un solo lado y dada corriente y ancho de escaneo. Cuanto más rápida sea la velocidad del transportador, menor será la dosis. Por ejemplo, si el D _sf requerido es de 1 kGy, entonces el transportador debe funcionar a 15.42 cm/s (9.25 m/min):

\( v=\frac{1.85\times10^{6}I_{a}}{wD_{sf}} = \frac{1.85\times10^{6}\times10^{-3}}{120\times1} = 15.42 \text{ cm/s} \)

Ejemplo\(\PageIndex{10}\)

Ejemplo 10: Cálculo de la tasa de rendimiento para un sistema de haz de electrones

Problema:

Calcular la tasa de rendimiento para la desinfestación por haz de electrones de papaya (dosis mínima requerida de 0.26 kGy) con una irradiación de haz de electrones (modo unilateral) con 12 kW de potencia y eficiencia de rendimiento de 0.5.

Solución

1. (a) Calcular la tasa de rendimiento con P = 12 kW, D = 0.26 kGy y η = 0.5.

   De la Ecuación 6.4.17:

\( \frac{dm}{dt}=\frac{\eta P}{D} \)

Entonces:\( \frac{dm}{dt} [\frac{kg}{s}]=\frac{0.5\times12[kW]}{0.26[kGy]} = 23.1\text{ kg/s} \)

1. (b) Suponiendo una densidad de área de 7 g/cm ² y un ancho de barrido de 120 cm, calcular la velocidad del transportador, v.

   Encuentra v usando la Ecuación 6.4.14:

\( v=\frac{dm/dt}{A_{d}w} \)

1. con A _d = 7 g/cm ², luego:

\( v=\frac{dm/dt}{A_{d}\times w} = \frac{23.1[\frac{kg}{s}]\times1000[\frac{kg}{g}]}{7[\frac{g}{cm^{2}}]\times 120[cm]} =27.5 \text{ cm/s} \)

1. (c) Si el producto está dispuesto en cajas de cartón (Figura 6.4.11), las cuales tienen un área de sección transversal de 7432 cm ², calcular la masa total de alimentos que deben colocarse en una caja

   Encuentra m usando la Ecuación 6.4.16:

\( m=A_{d}A_{c} \)

1. con A _d = 7 g/cm ² y A _c = 7432 cm ², luego:

\( m=A_{d}\times A_{c}=\frac{7[\frac{g}{cm^{2}}]\times7432[cm^{2}]}{1000[\frac{g}{kg}]}=52\ kg \)

1. El tratamiento de desinfestación de papaya (dosis de 0.26 kGy) usando un haz de electrones unilateral se puede lograr cuando se colocan 52 kg del alimento debajo de la viga eléctrica con el transportador funcionando a 27.5 cm/s.

Créditos de imagen

Figura 1. Moreira, R. G. (CC Por 4.0). (2020). Perfil de deposición de energía para electrones de 10 MeV en un absorbedor de agua (adaptado de Miller, 2005).

Figura 2. Moreira, R. G. (CC Por 4.0). (2020). Penetración dosis-profundidad para diferentes fuentes de radiación (rayos X, haces de electrones y rayos gamma) (adaptado del OIEA, 2015).

Figura 3. Moreira, R. G. (CC Por 4.0). (2020). Curvas típicas de profundidad-dosis para electrones de diversas energías en el rango aplicable a las operaciones de procesamiento de alimentos (adaptadas del OIEA, 2002).

Figura 4. Moreira, R. G. (CC Por 4.0). (2020). Profundidad: curva de dosis para electrones de 10 MeV en el agua, donde la dosis de entrada (superficie) es del 100% (adaptada del OIEA, 2002).

Figura 5. Moreira, R. G. (CC Por 4.0). (2020). Distribuciones de dosis de profundidad para electrones de 10 MeV en agua para configuraciones de un lado y de doble cara (DUR = 1.35).

Figura 6. Moreira, R. G. (CC Por 4.0). (2020). Grosor máximo de penetración para configuraciones de haz de electrones solo superior e inferior utilizando electrones de 10 MeV en agua (DUR = 1.35).

Figura 7. Moreira, R. G. (CC Por 4.0). (2020). Grosor máximo de penetración para irradiación de haz electrónico de doble cara usando electrones de 10 MeV en agua (DUR = 1.35).

Figura 8. Moreira, R. G. (CC Por 4.0). (2020). Curva típica de supervivencia que muestra comportamiento cinético de primer orden.

Figura 9. Moreira, R. G. (CC Por 4.0). (2020). Pasos necesarios para seleccionar la tecnología de irradiación adecuada para una aplicación de procesamiento de alimentos (adaptado de Miller, 2005).

Figura 10. Moreira, R. G. (CC Por 4.0). (2020). Diagrama de flujo de decisión para seleccionar el enfoque de irradiación correcto (adaptado de Miller, 2005). La MMR es el rango aceptable de proporciones de dosis máxima a mínima (DUR).

Figura 11. Moreira, R. G. (CC Por 4.0). (2020). Configuración típica de irradiación con haz de electrones.

Ejemplo 5. Moreira, R. G. (CC Por 4.0). (2020). Ejemplo 5.

Ejemplo 6. Moreira, R. G. (CC Por 4.0). (2020). Ejemplo 6.

Referencias

Attix, F. H. (1986). Introducción a la física radiológica y a la dosimetría radiológica. Nueva York, NY: Wiley Interscience Publ. doi.org/10.1002/9783527617135.

Becker, R. C., Bly, J. H., Cleland, M. R., & Farrell, J. P. (1979). Requisitos del acelerador para el procesamiento por haz de electrones. Radiat. Phys. Chem., 14 (3—6), 353—375. https://doi.org/10.1016/0146-5724(79)90075-X.

Browne, M. (2013). Física para la ingeniería y la ciencia (2da. ed.). Nueva York, NY: McGraw Hill/Schaum.

CDC. (2018). Incidencia preliminar y tendencias de infecciones con patógenos transmitidos comúnmente a través de los alimentos. Red de Vigilancia Activa de Enfermedades Transmitidas por Alimentos, Informe Semanal de Morbilidad y Mortalidad. 68 (16), 369—373. CDC. Recuperado de https://www.cdc.gov/mmwr/volumes/68/wr/mm6816a2.htm?s_cid=mm6816a2_w.

Cleland, M. R. (2005). Curso sobre aceleradores pequeños. 383—416 (CERN-2006-012). Zeegse, Países Bajos. https://doi.org/10.5170/CERN-2006-012.383.

Eustice, R. F. (2017). Situación global y aplicaciones comerciales de la irradiación de alimentos. Ch. 20. En I. C. F. R. Ferreira, A. L. Antonio, & Cabo Verde, S. (Eds.), Tecnologías de irradiación de alimentos. Conceptos, aplicaciones y resultados. Química, función y análisis de alimentos No. 4. Cambridge, U. K.: Real Sociedad de Química, Thomas Graham House.

Fan, X. (2012). Radiación ionizante. En V. M. Gomez-Lopez (Ed.), Descontaminación de productos frescos y mínimamente procesados. doi.org/10.1002/9781118229187.

FDA. (2018). Irradiación en la producción, procesamiento y manejo de alimentos. Código de Reglamentos Federales Título 21. 3, CFR179.26. Washington, DC: FDA. Recuperado de www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfcfr/cfrsearch. cfm≈fr=179 .26.

Health Canada. (2016). Resumen técnico. Evaluación de seguridad de Health Canada de irradiación de carne molida cruda fresca y congelada. Gobierno de Canadá, Salud Canadá. Recuperado de http://www.hc-sc.gc.ca/fn-an/securit/irridation/tech_sum_food_irradiation_aliment_som_tech-eng.php#toxicology.

IAGE. (2002). Dosimetría para irradiación de alimentos. Informes Técnicos Serie No. 409. Viena, Austria: Organismo Internacional de Energía Atómica. Recuperado de https://www-pub.iaea.org/MTCD/Publications/PDF/TRS409_scr.pdf.

IAGE. (2015). Manual de buenas prácticas en irradiación de alimentos. Informes Técnicos Serie No. 481. Viena, Austria: Organismo Internacional de Energía Atómica. Recuperado de https://www.iaea.org/publications/10801/manual-of-good-practice-in-food-irradiation.

ICGFI. (1999). Datos sobre la irradiación de alimentos. Sección de Protección Alimentaria y Ambiental. División Mixta FAO/OIEA de Técnicas Nucleares en Alimentación y Agricultura. Viena, Austria: Grupo Consultivo Internacional sobre Irradiación de Alimentos.

Lagunas-Solar, M. C. (1995). Procesamiento por radiación de alimentos: Una visión general de los principios científicos y el estado actual. J. Protección Alimentaria, 58 (2), 186—192. https://doi.org/10.4315/0362-028x-58.2.186.

Maherani, B., Hossain, F., Criado, P., Ben-Fadhel, Y., Salmieri, S., & Lacroix, M. (2016). Desarrollo del mercado mundial y aceptación por el consumidor de la tecnología de irradiación. Alimentos, 5 (4): 2—21. https://doi.org/10.3390/foods5040079.

Mahmoud, B. S. M., Bachman, G., & Linton, R. H. (2010). Inactivación de Escherichia coli O157:H7, Listeria monocytogenes, Salmonella enterica y Shigella flexneri en hojas de espinaca por rayos X. Microbiol alimentario., 27 (1), 24—28. https://doi.org/10.1016/j.fm.2009.07.004.

Miller, R. B. (2005). Irradiación electrónica de alimentos: Una introducción a la tecnología. Alimentos Ing. Serie. Nueva York, NY: Springer.

Morehouse, K. M., & Komolprasert, V. (2004). Irradiación de alimentos y empaques: Una visión general. Ch. 1. En K. M. Morehouse, & V. Komolprasert (Eds.), Irradiación de alimentos y empaques. Sociedad Americana de Química. Serie de Simposios ACS. https://doi.org/10.1021/bk-2004-0875.

Moreira, R. G., Puerta-Gómez, A. F., Kim, J., & Castell-Pérez, M. E. (2012). Factores que afectan los valores d de radiación (D10) de un cóctel de Escherichia coli y Salmonella typhimurium LT2 inoculados en productos frescos. J. Ciencia Alimentaria, 77 (4), E104-E111. doi.org/10.1111/j.1750-3841.2011.02603.x.

 

Niemira, B. A. (2007). Eficacia relativa del lavado de hipoclorito de sodio versus irradiación para inactivar Escherichia coli O157:H7 Internalizada en hojas de lechuga romana y espinacas crías. J. Protección Alimentaria, 70 (11), 2526—2532. https://doi.org/10.4315/0362-028x-70.11.2526.

Olaimat, A. N., & Holley, R. A. (2012). Factores que influyen en la seguridad microbiana de los productos frescos: Una revisión. Microbiol alimentario., 32 (1), 1—19. https://doi.org/10.1016/j.fm.2012.04.016.

Rajtowski, K. T., Boyd, G., & Thayer, D. W. (2003). Valores D de irradiación para Escherichia coli O157:H7 y Salmonella sp. sobre semillas de brócoli inoculadas y efectos de la irradiación sobre el brote de brócoli manteniendo la calidad y viabilidad de la semilla. J. Protección Alimentaria, 66 (5), 760—766. https://doi.org/10.4315/0362-028x-66.5.760.

Strydom, W., Parker, W., & Olivares, M. (2005). Haces de electrones: Aspectos físicos y clínicos. En E. Podgorsakt (Ed.), Física de oncología radioterápica: Un manual para profesores y alumnos. Viena, Austria: OIEA.

Thayer, D. W., Boyd, G., Muller, W. S., Lipson, C. A., Hayne, W. C., & Baer, S. H. (1990). Resistencia a la radiación de la salmonela. J. Ind. Microbiol., 5 (6), 383—390. doi: https://doi.org/10.1007/BF01578097.

Universidad de Wisconsin. (2019). El proceso de irradiación de los alimentos. Grupo de Educación de Irradiación de Alimentos UW. Recuperado de UW-Food-Irradiation.engr.wisc.edu/Materiales/fi_Process_Brochure.pdf.

USNRC. (2018). Comisión Reguladora Nuclear de Estados Unidos. Recuperado de https://www.nrc.gov/about-nrc/radiation/health-effects/radiation-basics.html.

QUIEN. (1981). La salubridad de los alimentos irradiados. Informe Técnico Serie 659. Ginebra, Suiza: Organización Mundial de la Salud. Recuperado de https://apps.who.int/iris/bitstream/handle/10665/41508/WHO_TRS_659.pdf?sequence=1&isAllowed=y.