1.5: Problemas de introducción

Última actualización
Guardar como PDF

Page ID: 85366

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Problemas de introducción a señales y sistemas.

Valores RMS

Se define que el valor rms (raíz cuadrática media) de una señal periódica es

\[s = \sqrt{\frac{1}{T}\int_{0}^{T}s^{2}(t)dt} \nonumber \]

donde T se define como el periodo de la señal: el número positivo más pequeño tal que

\[s(t)= s(t+T) \nonumber \]

¿Cuál es el periodo de

\[s(t)= A\sin (2\pi f_{0}t+\varphi ) \nonumber \]

¿Cuál es el valor rms de esta señal? ¿Cómo se relaciona con el valor pico?
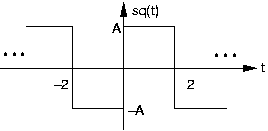
¿Cuál es el periodo y valor rms de la onda cuadrada representada, genéricamente denotada por sq (t)?

Al inspeccionar cualquier dispositivo que conectes a un enchufe de pared, verás que está etiquetado como “110 voltios CA”. ¿Cuál es la expresión para el voltaje proporcionado por un enchufe de pared? ¿Cuál es su valor rms?

Módems

La palabra “módem” es la abreviatura de “modulador-demodulador”. Los módems se utilizan no solo para conectar computadoras a líneas telefónicas, sino también para conectar fuentes digitales (de valor discreto) a canales genéricos. En este problema, exploramos un tipo simple de módem, en el que la información binaria se representa por la presencia o ausencia de una sinusoide (presencia que representa un “1" y ausencia un “0"). En consecuencia, la señal transmitida del módem que representa un solo bit tiene la forma

\[x(t)= A\sin (2\pi f_{0}t), 0\leq t\leq T \nonumber \]

Dentro de cada intervalo de bits T, la amplitud es A o cero.

¿Cuál es el intervalo de transmisión más pequeño que tiene sentido con la frecuencia f ₀?
Suponiendo que diez ciclos de la sinusoide comprenden el intervalo de transmisión de un solo bit, ¿cuál es la velocidad de datos de este esquema de transmisión? Ahora supongamos que en lugar de usar señalización “on-off”, permitimos uno de varios valores diferentes para la amplitud durante cualquier intervalo de transmisión. Si se utilizan N valores de amplitud, ¿cuál es la velocidad de datos resultante?
El diagrama de bloques de comunicaciones clásico se aplica al módem. Discutir cómo el transmisor debe interactuar con la fuente del mensaje ya que la fuente está produciendo letras del alfabeto, no bits.

Módems Avanzados

Para transmitir símbolos, como letras del alfabeto, los módems de computadora RU utilizan dos frecuencias (1600 y 1800 Hz) y varios niveles de amplitud. Una transmisión se envía por un periodo de tiempo T (conocido como el intervalo de transmisión o baudios) y es igual a la suma de dos portadoras ponderadas en amplitud.

\[x(t)= A_{1}\sin (2\pi f_{1}t) + A_{2}\sin (2\pi f_{2}t), 0\leq t\leq T \nonumber \]

Enviamos símbolos sucesivos eligiendo una combinación apropiada de frecuencia y amplitud, y enviándolos uno tras otro.

¿Cuál es el intervalo de transmisión más pequeño que tiene sentido usar con las frecuencias dadas anteriormente? En otras palabras, ¿qué debería ser T para que se produzca un número entero de ciclos de la portadora?
Esboce (usando Matlab) la señal que produce el módem a lo largo de varios intervalos de transmisión. Asegúrese de que los ejes estén etiquetados.
Usando su intervalo de transmisión de señal, ¿cuántos niveles de amplitud se necesitan para transmitir caracteres ASCII a una velocidad de datos de 3.200 bits/s? Asumir el uso del código ASCII extendido (8 bits).

Nota

Utilizamos un conjunto discreto de valores para A ₁y A ₂. _{Si tenemos N ₁ valores para la amplitud _A1, y N ₂ valores para A2, tenemos N ₁ N ₂ posibles símbolos que se pueden enviar durante cada intervalo de T segundos} . Para convertir este número en bits (la unidad fundamental que utilizan los ingenieros de información para calificar las cosas), compute:

\[\log _{2}(N_{1}N_{2}) \nonumber \]