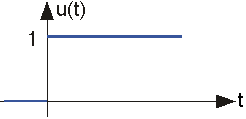2.2: Señales elementales

Objetivos de aprendizaje

• Las señales complejas se pueden construir a partir de señales elementales, incluyendo el exponencial complejo, paso de unidad, pulso, etc.
• Aprendiendo sobre las señales elementales.

Las señales elementales son los bloques de construcción con los que construimos señales complicadas. Por definición, las señales elementales tienen una estructura simple. Exactamente lo que queremos decir con la “estructura de una señal” se desplegará en esta sección del curso. Las señales no son más que funciones definidas con respecto a alguna variable independiente, que tomamos para ser tiempo en su mayor parte. Las señales muy interesantes no son funciones únicamente del tiempo; un gran ejemplo de lo cual es una imagen. Para ello, las variables independientes son x e y (espacio bidimensional). Las señales de video son funciones de tres variables: dos dimensiones espaciales y tiempo. Afortunadamente, la mayoría de las ideas que subyacen a la teoría moderna de la señal se pueden ejemplificar con señales unidimensionales.

Sinusoides

Quizás la señal de valor real más común es la sinusoide.

\[s(t) = A\cos (2\pi f_{0}t+\varphi ) \nonumber \]

Para esta señal,$\mathrm{<strong>A</strong>}$es su amplitud,${\mathrm{<strong>f</strong>}}_{}$${\mathrm{<strong>₀</strong>}}_{}$su frecuencia, y$\mathrm{<strong>\phi </strong>}$su fase.

Exponenciales Complejos

La señal más importante es de valor complejo, la exponencial compleja.

\[s(t) = Ae^{i(2\pi f_{0}t+\varphi )}\\ s(t) = Ae^{i\varphi }e^{i2\pi f_{0}t} \nonumber \]

Aquí,

\[Ae^{i\varphi } \: is\: the\: signal's\: \textbf{complex amplitude} \nonumber \]

Considerando la amplitud compleja como un número complejo en forma polar, su magnitud es la amplitud A y su ángulo la fase de la señal. La amplitud compleja también se conoce como fasor. El exponencial complejo no se puede descomponer aún más en señales más elementales, ¡y es la señal más importante en ingeniería eléctrica! Las manipulaciones matemáticas al principio parecen ser más difíciles porque se introducen números de valor complejo. De hecho, a principios del siglo XX, los matemáticos pensaban que los ingenieros no serían lo suficientemente sofisticados para manejar exponenciales complejos a pesar de que simplificaron enormemente la solución de problemas de circuitos. Steinmetz introdujo exponenciales complejos a la ingeniería eléctrica, y demostró que “meros” ingenieros podían utilizarlos con buenos resultados e incluso obtener respuestas correctas. Consulte Números complejos para una revisión de números complejos y aritmética compleja.

El exponencial complejo define la noción de frecuencia: es la única señal que contiene solo un componente de frecuencia. La sinusoide consta de dos componentes de frecuencia: uno a la frecuencia f ₀ y el otro a -f _0.

Relación Euler

Esta descomposición de la sinusoide se remonta a la relación de Euler.

\[\cos (2\pi ft) = \frac{e^{i2\pi ft}+e^{-(i2\pi ft)}}{2}\\ \sin (2\pi ft) = \frac{e^{i2\pi ft}-e^{-(i2\pi ft)}}{2i}\\ e^{i2\pi ft} = cos (2\pi ft)+i\: sin (2\pi ft) \nonumber \]

Descomposición

Así, la compleja señal exponencial puede escribirse en términos de sus partes real e imaginaria utilizando la relación de Euler. Así, las señales sinusoidales pueden expresarse como la parte real o imaginaria de una señal exponencial compleja, dependiendo la elección de si se necesita fase coseno o seno, o como la suma de dos exponenciales complejos. Estas dos descomposiciones son matemáticamente equivalentes entre sí.

\[A\cos (2\pi ft+\varphi ) = \Re (Ae^{i\varphi }e^{i2\pi ft})\\ A\sin (2\pi ft+\varphi ) = \Im (Ae^{i\varphi }e^{i2\pi ft}) \nonumber \]

Figura 2.2.1 Gráficamente, el complejo exponencial escribe un círculo en el plano complejo a medida que evoluciona el tiempo. Sus partes reales e imaginarias son sinusoides. La velocidad a la que la señal va alrededor del círculo es la frecuencia f y el tiempo que tarda en dar la vuelta es el periodo T. Una relación fundamental es T = 1/f

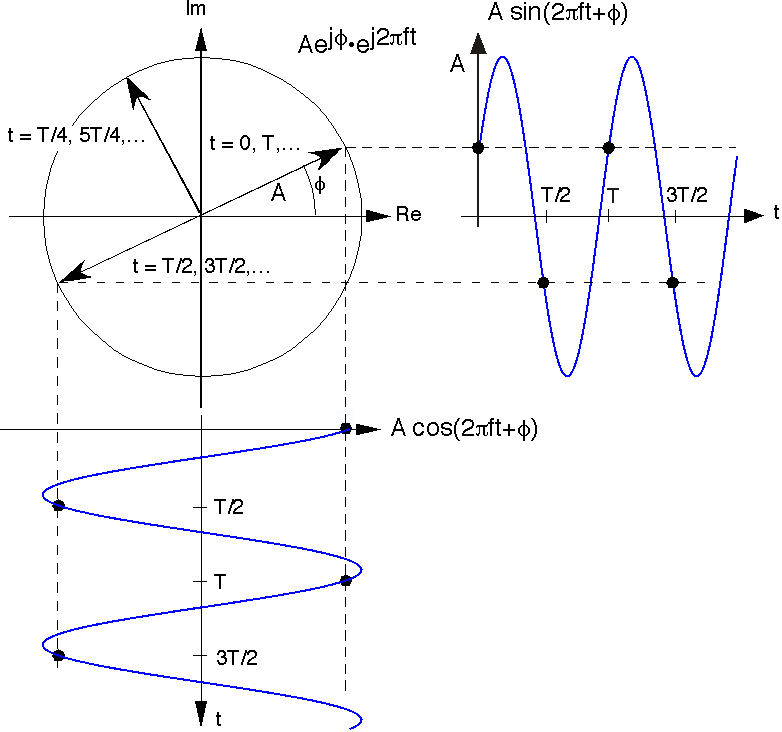
Usando el plano complejo, podemos imaginar las variaciones temporales del exponencial complejo como se ve en la figura anterior. La magnitud del exponencial complejo es A y el valor inicial del exponencial complejo a t = 0 tiene un ángulo de φ. A medida que aumenta el tiempo, el locus de puntos trazados por el exponencial complejo es un círculo (tiene una magnitud constante de A). El número de veces por segundo que damos la vuelta al círculo es igual a la frecuencia f. El tiempo que tarda el exponencial complejo en dar la vuelta al círculo una vez se conoce como su período T y es igual a 1/f. Las proyecciones sobre los ejes real e imaginario del vector giratorio que representa la señal exponencial compleja son la señal coseno y seno de la relación de Euler como se indicó anteriormente.

Exponenciales reales

A diferencia de los exponenciales complejos que oscilan, los exponenciales reales decaen.

\[s(t) = e^{-\frac{t}{\tau }} \nonumber \]

Figura 2.2.2 El exponencial real

La cantidad τ se conoce como la constante de tiempo del exponencial, y corresponde al tiempo requerido para que el exponencial disminuya en un factor de 1/e, que aproximadamente equivale a 0.368. Un exponencial complejo en descomposición es producto de un exponencial real y uno complejo.

\[s(t) = Ae^{i\varphi }e^{-\frac{t}{\tau }}e^{i2\pi ft}\\ s(t) = Ae^{i\varphi }e^{\left ( -\frac{t}\tau +i2\pi f \right )t} \nonumber \]

En el plano complejo, esta señal corresponde a una espiral exponencial. Para tales señales, podemos definir la frecuencia compleja como la cantidad multiplicando t.

Paso de Unidad

La función de paso de unidad se denota con u (t) y se define como

\[u(t) = 0\, \, if \,\, t< 0\\ u(t) = 1\, \: if \, \, t> 0 \nonumber \]

Figura 2.2.3 Paso unitario

Advertencia de origen

Esta señal es discontinua en el origen. Su valor en el origen no necesita ser definido, y no importa en la teoría de la señal.

Este tipo de señal se utiliza para describir señales que “se encienden” de repente. Por ejemplo, para representar matemáticamente encender un oscilador, podemos escribirlo como el producto de una sinusoide y un paso:

\[s(t) = A\sin (2\pi ft)u(t) \nonumber \]

Pulso

El pulso unitario describe encender una señal de amplitud unitaria por una duración de Δ segundos y luego apagarla.

\[p\Delta (t) = 0\; if\; t< 0\\ p\Delta (t) = 1\; if\; 0< t< \Delta \\ p\Delta (t) = 0\; if\; t> \Delta \nonumber \]

Figura 2.2.4 El pulso

Encontraremos que esta es la segunda señal más importante en las comunicaciones.

Onda Cuadrada

La onda cuadrada sq (t) es una señal periódica como la sinusoide. También tiene una amplitud y un periodo, los cuales deben especificarse para caracterizar la señal. Posteriormente encontramos que la onda sinusoidal es una señal más simple que la onda cuadrada.

Figura 2.2.5 La onda cuadrada