2.7: Problemas de señales y sistemas
- Page ID
- 85596
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Problemas de práctica de Señales y Sistemas.
Aritmética de números complejos
Encuentra la parte real, la parte imaginaria, la magnitud y el ángulo de los números complejos dados por las siguientes expresiones.
- -1
- \[\frac{1+\sqrt{3}i}{2} \nonumber \]
- \[1+i+e^{i\tfrac{\pi }{2}} \nonumber \]
- \[e^{i\tfrac{\pi }{3}}+e^{i\pi }+e^-({i\tfrac{\pi }{3}}) \nonumber \]
Descubriendo las raíces
Los números complejos exponen todas las raíces de los números reales (y complejos). Por ejemplo, debe haber dos raíces cuadrados, tres raíces cúbicas, etc. de cualquier número. Encuentra las siguientes raíces.
- ¿Cuáles son las raíces cúbicas de 27? Es decir, ¿qué es 27 1/3?
- ¿Cuáles son las quintas raíces de 3 (3 1/5)?
- ¿Cuáles son las cuartas raíces de una?
Exponenciales geniales
- \[i^{i} \nonumber \]
- \[i^{2i} \nonumber \]
- \[i^{i^{-1}} \nonumber \]
Señales de valor complejo
Los números complejos y los fasores juegan un papel muy importante en la ingeniería eléctrica. Resolver sistemas para exponenciales complejos es mucho más fácil que para sinusoides, y el análisis de sistemas lineales es particularmente fácil.
- Encuentra la representación fasorial para cada uno, y vuelve a expresar cada uno como las partes real e imaginaria de un exponencial complejo. ¿Cuál es la frecuencia (en Hz) de cada uno? En general, ¿tus respuestas son únicas? Si es así, demuéstralo; si no, encuentra una respuesta alternativa para la compleja representación exponencial.
- \[3\sin (24t) \nonumber \]
- \[\sqrt{2} \cos \left ( 2\pi 60t + \frac{\pi }{4} \right ) \nonumber \]
- \[2 \cos \left (t + \frac{\pi }{6} \right ) + 4 \sin \left ( t - \frac{\pi }{3} \right ) \nonumber \]
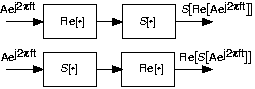
- Mostrar que para los sistemas lineales que tienen salidas de valor real para entradas reales, que cuando la entrada es la parte real de un exponencial complejo, la salida es la parte real de la salida del sistema a la exponencial compleja (ver figura a continuación).
\[S\left ( \Re (Ae^{i2\pi ft}) \right ) = \Re \left (S (Ae^{i2\pi ft}) \right ) \nonumber \]
- Para cada uno de los voltajes indicados, escríbelo como la parte real de un exponencial complejo Indique\[v(t) = \Re (Ve^{st}) \nonumber \] explícitamente el valor de la amplitud compleja V y la frecuencia compleja s. representar cada amplitud compleja como un vector en el plano V, e indicar la ubicación de las frecuencias en el plano s complejo.
- \[v(t) = \cos (5t) \nonumber \]
- \[v(t) = \sin \left ( 8t+\frac{\pi }{4} \right ) \nonumber \]
- \[v(t) = e^{-t} \nonumber \]
- \[v(t) = e^{-(3t)}\sin \left ( 4t+\frac{3\pi }{4} \right ) \nonumber \]
- \[v(t) = 5e^{(2t)}\sin (8t + 2\pi ) \nonumber \]
- \[v(t) = -2 \nonumber \]
- \[v(t) = 4\sin (2t) + 3\cos (2t) \nonumber \]
- \[v(t) = 2\cos \left ( 100\pi t + \frac{\pi }{6} \right )- \sqrt{3}\sin \left ( 100\pi t + \frac{\pi }{2} \right ) \nonumber \]
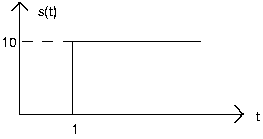
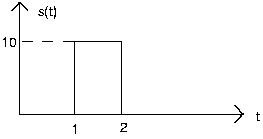
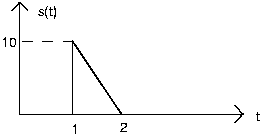
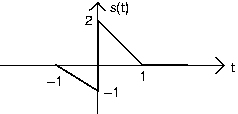
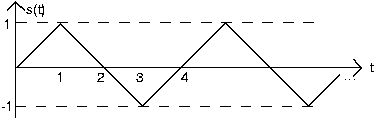
- Expresar cada una de las siguientes señales como una combinación lineal de funciones de paso retardadas y ponderadas y rampas (la integral de un paso).
Lineales, Sistemas invariantes en el tiempo
Cuando la entrada a un sistema lineal, invariable en el tiempo es la señal x (t), la salida es la señal y (t),
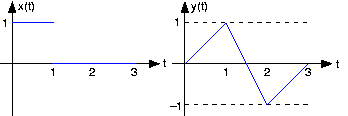
- Encuentra y dibuja la salida de este sistema cuando la entrada es la señal representada:
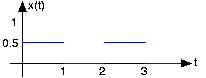
- Encuentre y dibuje la salida de este sistema cuando la entrada es un paso de unidad.
Sistemas Lineales
La entrada representada x (t) a un sistema lineal, invariable en el tiempo, produce la salida y (t).
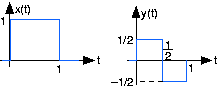
- ¿Cuál es la salida del sistema a una entrada de paso de unidad u (t)?
- Cuál será la salida cuando la entrada sea la onda cuadrada representada:
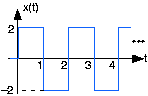
Canal de Comunicación
Un canal de comunicación particularmente interesante puede modelarse como un sistema lineal, invariable en el tiempo. Cuando la señal transmitida x (t) es un pulso, la señal recibida r (t) es como se muestra:
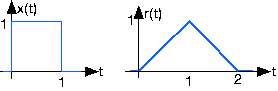
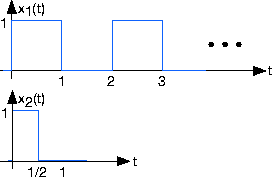
- ¿Cuál será la señal recibida cuando el transmisor envíe la secuencia de pulsos x 1 (t)?
- ¿Cuál será la señal recibida cuando el transmisor envíe la secuencia de pulsos x 2 (t) que tiene la mitad de duración que la original?
Computadoras Analógicas
Las llamadas computadoras analógicas utilizan circuitos para resolver problemas matemáticos, particularmente cuando involucran ecuaciones diferenciales. Supongamos que se nos da la siguiente ecuación diferencial para resolver.
\[\frac{\mathrm{d\: y(t)} }{\mathrm{d} t} + ay(t) = x(t) \nonumber \]
En esta ecuación, a es una constante.
- Cuando la entrada es un paso unitario\[(x(t) = u(t)) \nonumber \] la salida viene dada por\[y(t) = (1-e^{-(at)})u(t) \nonumber \] ¿Cuál es la energía total gastada por la entrada?
- En lugar de un paso unitario, supongamos que la entrada es un pulso unitario (unidad-amplitud, unidad-duración) entregado al circuito en el tiempo t =10, ¿cuál es el voltaje de salida en este caso? Croquis de la forma de onda