2.6: Sistemas simples
- Page ID
- 85579
- Los sistemas manipulan señales.
- Hay algunos sistemas simples que realizarán funciones simples sobre las señales. Los ejemplos incluyen amplificación (o atenuación), inversión de tiempo, retardo y diferenciación/integración.
Los sistemas manipulan señales, creando señales de salida derivadas de sus entradas. Por qué los siguientes son categorizados como “simples” sólo se harán evidentes hacia el final del curso.
Fuentes
Las fuentes producen señales sin tener entrada. Nos gusta pensar en estos como que tienen parámetros controlables, como amplitud y frecuencia. Ejemplos serían los osciladores que producen señales periódicas como sinusoides y ondas cuadradas y generadores de ruido que producen señales con formas de onda erráticas (más sobre el ruido posteriormente). Simplemente escribir una expresión para las señales que producen especifica fuentes. Un generador de onda sinusoidal podría especificarse por:
\[y(t) = A\sin (2\pi f_{0}t)u(t) \nonumber \]
La ecuación anterior dice que la fuente se encendió a t =0 para producir una sinusoide de amplitud A y frecuencia f 0.
Amplificadores
Un amplificador multiplica su entrada por una constante conocida como ganancia del amplificador.
\[y(t) = Gx(t) \nonumber \]
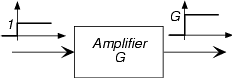
La ganancia puede ser positiva o negativa (si es negativa, diríamos que el amplificador invierte su entrada) y su magnitud puede ser mayor que uno o menor que uno. Si es menor de uno, el amplificador realmente atenúa. Un ejemplo del mundo real de un amplificador es el estéreo de tu hogar. Usted controla la ganancia girando el control de volumen.
Retraso
Un sistema sirve como un retardo de tiempo cuando la señal de salida es igual a la señal de entrada en un momento anterior.
\[y(t) = x(t-\tau ) \nonumber \]
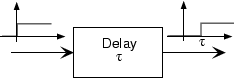
Aquí, τ es el retraso. La manera de entender este sistema es enfocarse en el origen del tiempo: La salida en el tiempo t = τ es igual a la entrada en el tiempo t = 0 Así, si el retraso es positivo, la salida emerge más tarde que la entrada, y trazando la salida equivale a desplazar la gráfica de entrada hacia la derecha. El retraso puede ser negativo, en cuyo caso decimos que el sistema avanza su entrada. Dichos sistemas son difíciles de construir (tendrían que producir valores de señal derivados de lo que será la entrada), pero tendremos ocasión de avanzar las señales a tiempo.
Reversión de tiempo
Aquí, la señal de salida es igual a la señal de entrada volteada sobre el origen del tiempo.
\[y(t) = x(-t) \nonumber \]
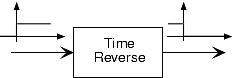
Nuevamente, tales sistemas son difíciles de construir, pero la noción de inversión del tiempo ocurre con frecuencia en los sistemas de comunicaciones.
Se mencionó anteriormente la cuestión de si el orden de los sistemas importaba. Es decir, si tenemos dos sistemas en cascada, ¿depende la salida de cuál viene primero? Determinar si el orden importa para la cascada de un amplificador y un retardo y para la cascada de un sistema de inversión de tiempo y un retardo.
Solución
En el primer caso, el orden no importa; en el segundo sí. “Retraso” significa t → t - τ. “Tiempo inverso” significa t → -t.
Caso 1
\[y(t) = Gx(t-\tau ) \nonumber \]
La forma en que aplicamos la ganancia y retardamos la señal da el mismo resultado.
Caso 2
- Tiempo inverso y luego retardo:
\[y(t) = x\left ( - (t-\tau )\right ) = x(-t+\tau ) \nonumber \]
- Retraso y luego tiempo inverso:
\[y(t) = x\left ( (-t)-\tau )\right ) \nonumber \]
Sistemas Derivados e Integradores
Los sistemas que realizan operaciones similares a cálculos en sus entradas pueden producir formas de onda significativamente diferentes a las presentes en la entrada. Los sistemas derivados operan de manera directa: Un sistema de primera derivada tendría la relación insumo-producto
\[y(t) = \frac{\mathrm{d} }{\mathrm{d} t}x(t) \nonumber \]
Los sistemas integrales tienen la complicación de que se deben definir los límites de la integral. Es una convención de teoría de señales que la operación integral elemental tiene un límite inferior de\(-\infty \nonumber \) y que el valor de todas las señales\(t = -\infty \nonumber \) es igual a cero. Un integrador simple tendría relación entrada-salida:
\[y(t) = \int_{-\infty }^{t}x(\alpha )d\alpha \nonumber \]
Sistemas Lineales
Los sistemas lineales son una clase de sistemas en lugar de tener una relación específica de entrada/salida. Los sistemas lineales forman la base de la teoría de sistemas, y son la clase de sistemas más importante en las comunicaciones. Tienen la propiedad de que cuando la entrada se expresa como una suma ponderada de señales componentes, la salida es igual a la misma suma ponderada de las salidas producidas por cada componente. Cuando S (•) es lineal,
\[S\left ( G_{1}x_{1}(t)+ G_{2}x_{2}(t) \right ) = G_{1}S(x_{1}(t))+ G_{2}S(x_{2}(t)) \nonumber \]
para todas las opciones de señales y ganancias.
Esta propiedad general de relación entrada-salida se puede manipular para indicar propiedades específicas compartidas por todos los sistemas lineales.
\[S(Gx(t)) = GS(x(t)) \nonumber \]
El coloquialismo que resume esta propiedad es “El doble de entrada, se duplica la salida”. Tenga en cuenta que esta propiedad es consistente con formas alternativas de expresar cambios de ganancia: Dado que 2x (t) también es igual a x (t) +x (t), la definición del sistema lineal proporciona la misma salida sin importar cuál de estos se use para expresar una señal dada.
\[S(0) = 0 \nonumber \]
Si la entrada es idéntica a cero para todos los tiempos, la salida de un sistema lineal debe ser cero. Esta propiedad se desprende de la simple derivación:
\[S(0) = S(x(t)-x(t)) = S(x(t)) - S(x(t)) = 0 \nonumber \]
Justo por qué los sistemas lineales son tan importantes está relacionado no sólo con sus propiedades, que se divulgan a lo largo de este curso, sino también porque se prestan a un análisis matemático relativamente simple. Dijo de otra manera: “¡Son los únicos sistemas que entendemos a fondo!”
Podemos encontrar la salida de cualquier sistema lineal a una entrada complicada descomponiendo la entrada en señales simples. La ecuación anterior dice que cuando un sistema es lineal, su salida a una entrada descompuesta es la suma de salidas a cada entrada. por ejemplo si,
\[x(t) = e^{-t} + \sin (2\pi f_{0}t) \nonumber \]
La salida S (x (t)) de cualquier sistema lineal es igual
\[y(t) = S(e^{-t}) + S(\sin (2\pi f_{0}t)) \nonumber \]
Sistemas invariantes en el tiempo
Se dice que los sistemas que no cambian su relación entrada-salida con el tiempo son invariantes en el tiempo. La forma matemática de afirmar esta propiedad es utilizar el concepto de retardo de señal descrito anteriormente en Simple Systems.
\[(y(t) = S(x(t))) \Rightarrow (y(t-\tau ) = S(x(t-\tau ))) \nonumber \]
Si retrasa (o avanza) la entrada, la salida se retrasa de manera similar (avanzada). Por lo tanto, un sistema invariable en el tiempo responde a una entrada que puede suministrar mañana de la misma manera que responde a la misma entrada aplicada hoy; la salida de hoy simplemente se retrasa para que ocurra mañana.
La colección de sistemas lineales invariantes en el tiempo son los sistemas más entendidos. Gran parte del procesamiento de señales y la teoría de sistemas discutidos aquí se concentra en tales sistemas. Por ejemplo, los circuitos eléctricos son, en su mayor parte, lineales e invariables en el tiempo. Abundan los no lineales, pero caracterizarlos para que puedas predecir su comportamiento para cualquier entrada sigue siendo un problema sin resolver.
