3.1: Voltaje, corriente y elementos de circuito genéricos
- Page ID
- 85457
- Aprende sobre diversas señales como voltaje y corriente.
- Los sistemas que se utilizan para manipular señales se denominan circuitos.
Sabemos que la información puede ser representada por señales; ahora necesitamos entender cómo se realizan físicamente las señales. A lo largo de los años, se ha encontrado que las señales eléctricas son las más fáciles de usar. El voltaje y las corrientes comprenden las instancias eléctricas de las señales. Así, necesitamos adentrarnos en el mundo de la electricidad y el electromagnetismo. Los sistemas utilizados para manipular señales eléctricas directamente se denominan circuitos, y refinan la representación de la información o extraen información de la tensión o corriente. En muchos casos, hacen buenos ejemplos de sistemas lineales.
Un elemento de circuito genérico coloca una restricción entre las variables clásicas de un circuito: voltaje y corriente. El voltaje es potencial eléctrico y representa el “empuje” que impulsa la carga eléctrica de un lugar a otro. Lo que hace que la carga se mueva es una separación física entre carga positiva y negativa. Una batería genera, a través de medios electroquímicos, exceso de carga positiva en un terminal y carga negativa en el otro, creando un campo eléctrico. El voltaje se define a través de un elemento de circuito, con el signo positivo denotando una caída de voltaje positiva a través del elemento. Cuando un conductor conecta los potenciales positivos y negativos, la corriente fluye, con corriente positiva que indica que la carga positiva fluye desde el terminal positivo al negativo. Los electrones comprenden el flujo de corriente en muchos casos. Debido a que los electrones tienen una carga negativa, los electrones se mueven en la dirección opuesta al flujo de corriente positiva: La carga negativa que fluye hacia la derecha equivale a la carga positiva que se mueve hacia la izquierda.
Es importante entender la física del flujo de corriente en conductores para apreciar la innovación de los nuevos dispositivos electrónicos. La carga eléctrica puede surgir de muchas fuentes, siendo la más simple el electrón. Cuando decimos que “los electrones fluyen a través de un conductor”, lo que queremos decir es que los átomos constituyentes del conductor renuncian libremente a los electrones de sus cáscaras externas. “Flujo” significa así que los electrones saltan de átomo a átomo impulsados por el potencial eléctrico aplicado. Un electrón faltante, sin embargo, es una carga positiva virtual. Los ingenieros eléctricos llaman a estos agujeros, y en algunos materiales, particularmente ciertos semiconductores, el flujo de corriente se debe en realidad a los agujeros. El flujo de corriente también ocurre en las células nerviosas que se encuentran en su cerebro. Aquí, las neuronas “se comunican” usando pulsos de voltaje propagantes que dependen del flujo de iones positivos (potasio y sodio principalmente, y hasta cierto punto calcio) a través de la pared externa de la neurona. Así, la corriente puede provenir de muchas fuentes, y la teoría de circuitos se puede utilizar para entender cómo fluye la corriente en reacción a los campos eléctricos.
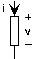
La corriente fluye a través de elementos de circuito, como el representado en la figura anterior, y a través de conductores, los cuales indicamos por líneas en diagramas de circuitos. Para cada elemento del circuito definimos una tensión y una corriente. El elemento tiene una relación v-i definida por las propiedades físicas del elemento. Al definir la relación v-i, tenemos la convención de que la corriente positiva fluye de caída de voltaje positiva a negativa. El voltaje tiene unidades de voltios, y tanto la unidad como la cantidad se llaman por Volta. La corriente tiene unidades de amperios, y lleva el nombre del físico francés Ampère.
Los voltajes y corrientes también llevan energía. Nuevamente utilizando la convención mostrada en la Figura 3.1.1 para elementos de circuito, la potencia instantánea en cada momento de tiempo consumida por el elemento viene dada por el producto de la tensión y la corriente.
\[p(t) = v(t)i(t) \nonumber \]
Un valor positivo para la potencia indica que en el momento
\[E(t) = \int_{-\infty }^{t}p(\alpha )d\alpha \nonumber \]
Nuevamente, la energía positiva corresponde a la energía consumida y la energía negativa corresponde a la producción de energía. Tenga en cuenta que un elemento de circuito que tenga un perfil de potencia que sea tanto positivo como negativo durante algún intervalo de tiempo podría consumir o producir energía de acuerdo con el signo de la integral de potencia. Las unidades de energía son julios ya que un vatio equivale a julios/segundo.
Las facturas de energía residencial suelen indicar el uso de energía de una casa en kilovatios-hora. ¿Es esto realmente una unidad de energía? Si es así, ¿cuántos julios equivale a un kilovatio-hora?
Solución
Un kilovatio-hora equivale a 3,600,000 vatios-segundo, lo que de hecho corresponde directamente a 3,600,000 julios.