3.2: Elementos de Circuito Ideal
- Page ID
- 85512
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Este módulo proporciona ejemplos de los elementos elementales del circuito; la resistencia, el condensador y el inductor, que proporcionan relaciones lineales entre voltaje y corriente.
Los elementos elementales del circuito (la resistencia, el condensador y el inductor) imponen relaciones lineales entre voltaje y corriente.
Resistor
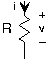
La resistencia es de lejos el elemento de circuito más simple. En una resistencia, el voltaje es proporcional a la corriente, con la constante de proporcionalidad R, conocida como la resistencia.
\[v(t) = R\, i(t) \nonumber \]
La resistencia tiene unidades de ohmios, denotadas por Ω, llamadas así por el científico eléctrico alemán Georg Ohm. En ocasiones, la relación v-i para la resistencia se escribe i = Gv, con G, la conductancia, igual a 1/R. La conductancia tiene unidades de Siemens (S), y lleva el nombre del industrial alemán de electrónica Werner von Siemens.
Cuando la resistencia es positiva, como lo es en la mayoría de los casos, una resistencia consume energía. El consumo de energía instantáneo de una resistencia se puede escribir de dos maneras.
\[p(t) = R\, i^{2}(t) = \frac{1}{R}v^{2}(t) \nonumber \]
A medida que la resistencia se acerca al infinito, tenemos lo que se conoce como un circuito abierto: No fluye corriente pero puede aparecer un voltaje distinto de cero a través del circuito abierto. A medida que la resistencia se vuelve cero, el voltaje va a cero para un flujo de corriente distinto de cero. Esta situación corresponde a un cortocircuito. Un superconductor realiza físicamente un cortocircuito.
Capacitor
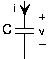
\[i = C\frac{\mathrm{d} v(t)}{\mathrm{d} t} \nonumber \]
El condensador almacena carga y la relación entre la carga almacenada y el voltaje resultante es q = Cv. La constante de proporcionalidad, la capacitancia, tiene unidades de faradios (F), y lleva el nombre del físico experimental inglés Michael Faraday. Como la corriente es la tasa de cambio de carga, la relación v-i se puede expresar en forma diferencial o integral.
\[i(t) = C\frac{\mathrm{d} v(t)}{\mathrm{d} t}\; or\; v(t) = \frac{1}{C}\int_{-\infty }^{t}i(\alpha )d\alpha \nonumber \]
Si el voltaje a través de un condensador es constante, entonces la corriente que fluye hacia él es igual a cero. En esta situación, el condensador es equivalente a un circuito abierto. La potencia consumida/producida por una tensión aplicada a un condensador depende del producto de la tensión y su derivada.
\[p(t) = Cv(t)\frac{\mathrm{d} v(t)}{\mathrm{d} t} \nonumber \]
Este resultado significa que el gasto total de energía de un condensador hasta el tiempo t está dado de manera concisa por
\[E(t) = \frac{1}{2}Cv^{2}(t) \nonumber \]
Esta expresión presume el supuesto fundamental de la teoría de circuitos: todos los voltajes y corrientes en cualquier circuito eran cero en el pasado lejano (t = - ∞).
Inductor
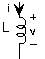
\[v = L\frac{\mathrm{d} i(t)}{\mathrm{d} t} \nonumber \]
El inductor almacena flujo magnético, con inductores de mayor valor capaces de almacenar más flujo. La inductancia tiene unidades de henries (H), y lleva el nombre del físico estadounidense Joseph Henry. Las formas diferenciales e integrales de la relación v-i del inductor son
\[v(t) = L\frac{\mathrm{d} i(t)}{\mathrm{d} t}\; or\; i(t) = \frac{1}{L}\int_{-\infty }^{t}v(\alpha )d\alpha \nonumber \]
La potencia consumida/producida por un inductor depende del producto de la corriente del inductor y su derivada
\[p(t) = Li(t)\frac{\mathrm{d} i(t)}{\mathrm{d} t} \nonumber \]
y su gasto total de energía hasta el momento
\[E(t) = \frac{1}{2}Li^{2}(t) \nonumber \]
Fuentes
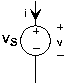
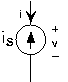
Las fuentes de voltaje y corriente también son elementos de circuito, pero no son lineales en el sentido estricto de los sistemas lineales. Por ejemplo, la relación v-i de la fuente de voltaje es v=v s independientemente de cuál sea la corriente. En cuanto a la fuente de corriente, i=-i s independientemente de la tensión. Otro nombre para una fuente de voltaje de valor constante es una batería, y se puede comprar en cualquier supermercado. Las fuentes actuales, por otro lado, son mucho más difíciles de adquirir; más adelante aprenderemos por qué.


