3.9: El concepto de impedancia
- Page ID
- 85523
- Discutir los resultados si todas las fuentes en el circuito son exponenciales complejas.
En lugar de resolver la ecuación diferencial que surge en los circuitos que contienen condensadores e inductores, pretendamos que todas las fuentes en el circuito son exponenciales complejos que tienen la misma frecuencia. Si bien esta pretensión sólo puede ser matemáticamente cierta, esta ficción va a facilitar enormemente la solución del circuito sin importar cuál sea realmente la fuente.
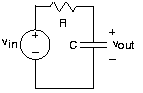
Para el circuito RC de ejemplo anterior, vamos
\[v_{in}=V_{in}e^{i2\pi ft} \nonumber \]
La amplitud compleja V in determina el tamaño de la fuente y su fase. La consecuencia crítica de asumir que las fuentes tienen esta forma es que todos los voltajes y corrientes en el circuito también son exponenciales complejos, teniendo amplitudes gobernadas por KVL, KCL, y las relaciones v-i y la misma frecuencia que la fuente. Para apreciar por qué esto debería ser cierto, investiguemos cómo se comporta cada elemento del circuito cuando ya sea el voltaje o la corriente es un exponencial complejo. Para la resistencia,
\[v=Ri \nonumber \]
Cuando
\[v=Ve^{i2\pi ft} \nonumber \]
Entonces
\[i=\frac{V}{R}e^{i2\pi ft} \nonumber \]
Así, si el voltaje de la resistencia es un exponencial complejo, también lo es la corriente, con una amplitud\[I=\frac{V}{R} \nonumber \] (determinada por la relación v-i de la resistencia) y una frecuencia igual a la tensión. Claramente, si se asumiera que la corriente era un exponencial complejo, también lo haría el voltaje. Para un condensador,
\[i=C\frac{\mathrm{d} v}{\mathrm{d} t} \nonumber \]
Dejando que el voltaje sea un exponencial complejo, tenemos:
\[i=CVi2\pi fe^{i2\pi ft} \nonumber \]
La amplitud de este complejo exponencial es:
\[I=CVi2\pi f \nonumber \]
Por último, para el inductor, donde
\[v=L\frac{\mathrm{d} i}{\mathrm{d} t} \nonumber \]A
Suponiendo que la corriente sea un exponencial complejo da como resultado que el voltaje tenga la forma:
\[v=LIi2\pi fe^{i2\pi ft} \nonumber \]
Su amplitud compleja viene dada por:
\[V=LIi2\pi f \nonumber \]
La principal consecuencia de asumir voltaje y corrientes exponenciales complejas es que la relación\[Z=\frac{V}{I} \nonumber \] para cada elemento no depende del tiempo, sino que depende de la frecuencia de la fuente. Esta cantidad se conoce como impedancia del elemento.
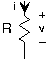
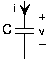
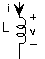
Resistencia Z R =R Condensador Z c =1/i2 πFC π 2 π 2 Inductor Z L = i2 πFL
Figura 3.9.2 Impedancia
La impedancia es, en general, una cantidad de valor complejo, dependiente de la frecuencia. Por ejemplo, la magnitud de la impedancia del condensador está inversamente relacionada con la frecuencia y tiene una fase de − π 2 - π/2. Esta observación significa que si la corriente es un exponencial complejo y tiene amplitud constante, la amplitud de la tensión disminuye con la frecuencia.
Consideremos las leyes de circuito de Kirchoff. Cuando los voltajes alrededor de un bucle son exponenciales complejos de la misma frecuencia, tenemos:
\[\sum_{nN}v_{n}=\sum_{nN}V_{n}e^{i2\pi ft}=0 \nonumber \]
lo que significa
\[\sum_{nN}v_{n}=0 \nonumber \]
las amplitudes complejas de los voltajes obedecen a KVL. Podemos imaginar fácilmente que las complejas amplitudes de las corrientes obedecen a KCL.
Lo que hemos descubierto es que la fuente (es) que iguala (n) un exponencial complejo de la misma frecuencia obliga a todas las variables del circuito a ser exponenciales complejos de la misma frecuencia. En consecuencia, la relación de voltaje a corriente para cada elemento es igual a la relación de sus amplitudes complejas, que depende únicamente de la frecuencia de la fuente y los valores de los elementos.
Esta situación se produce porque los elementos del circuito son lineales e invariables en el tiempo. Por ejemplo, supongamos que teníamos un elemento de circuito donde el voltaje igualaba al cuadrado de la corriente:
\[v(t)=Ki^{2}(t) \nonumber \]
Si
\[i(t)=Ie^{i2\pi ft}\\ v(t)=KI^{2}e^{i2\pi 2ft} \nonumber \]
lo que significa que el voltaje y la corriente ya no tenían la misma frecuencia y que su relación dependía del tiempo.
Porque para los elementos de circuito lineal la amplitud compleja del voltaje es proporcional a la amplitud compleja de la corriente:
\[V=ZI \nonumber \]
asumiendo fuentes exponenciales complejas significa que los elementos del circuito se comportan como si fueran resistencias, donde en lugar de resistencia, usamos impedancia. Debido a que las amplitudes complejas de voltaje y corriente también obedecen a las leyes de Kirchoff, podemos resolver circuitos usando el divisor de voltaje y corriente y las reglas de combinación en serie y paralelo considerando que los elementos son impedancias.