4.5: Aproximación de señales en serie de Fourier

Objetivos de aprendizaje

• Aproximaciones de series de Fourier.

Es interesante considerar la secuencia de señales que obtenemos a medida que incorporamos más términos a la aproximación de la serie de Fourier de la onda sinusoidal rectificada de media onda. Define s _K (t) para que sea la señal que contiene K+1 términos de Fourier.

\[s_{K}(t)=a_{0}+\sum_{k=1}^{K}a_{k}\cos \left ( \frac{2\pi kt}{T} \right )+ \sum_{k=1}^{K}b_{k}\sin \left ( \frac{2\pi kt}{T} \right ) \nonumber \]

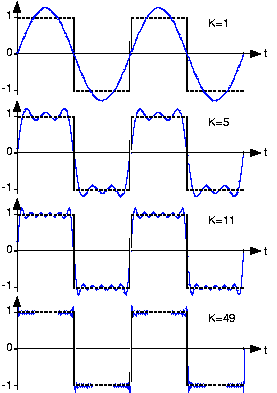
La Figura 4.5.1 a continuación muestra cómo esta secuencia de señales retrata la señal con mayor precisión a medida que se agregan más términos.

Figura 4.5.1 El espectro de la serie de Fourier de una sinusoide rectificada de media onda se muestra en la porción superior.

El índice indica el múltiplo de la frecuencia fundamental a la que la señal tiene energía. El efecto acumulativo de agregar términos a la serie de Fourier para la onda sinusoidal rectificada de media onda se muestra en la parte inferior. La línea discontinua es la señal real, con la línea continua mostrando la aproximación de series finitas al número indicado de términos, K+1.

Necesitamos evaluar cuantitativamente la precisión de la aproximación de la serie de Fourier para poder juzgar la rapidez con la que la serie se acerca a la señal. Cuando usamos un

\[\varepsilon _{K}(t)=\sum_{k=K+1}^{\infty }a_{k}\cos \left ( \frac{2\pi kt}{T} \right )+ \sum_{k=K+1}^{\infty }b_{k}\sin \left ( \frac{2\pi kt}{T} \right ) \nonumber \]

Para encontrar el error rms, debemos cuadrar esta expresión e integrarla a lo largo de un periodo. Nuevamente, la integral de la mayoría de los términos cruzados es cero, dejando

\[rms(\varepsilon _{K})=\sqrt{\frac{1}{2}\sum_{k=K+1}^{\infty }a_{k}^{2}+b_{k}^{2}} \nonumber \]

La Figura 4.5.2 muestra cómo disminuye el error en la serie de Fourier para la sinusoide rectificada de media onda a medida que se incorporan más términos. En particular, el uso de cuatro términos, como se muestra en la gráfica inferior de la Figura 4.5.1, tiene un error rms (relativo al valor rms de la señal) de aproximadamente 3%. La serie de Fourier en este caso converge rápidamente a la señal.

Figura 4.5.2 Error de aproximación para una sinusoide rectificada de media onda

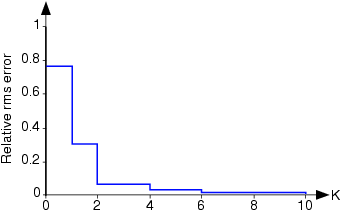
El error rms calculado de acuerdo con la ecuación anterior se muestra como una función del número de términos en la serie para la sinusoide rectificada de media onda. El error ha sido normalizado por el valor rms de la señal.

Podemos observar la Figura 4.5.3 para ver el espectro de potencia y el error de aproximación rms para la onda cuadrada.

Figura 4.5.3 La gráfica superior muestra el espectro de potencia de la onda cuadrada, y la gráfica inferior el error rms de la aproximación de la serie de Fourier de longitud finita a la onda cuadrada. El asterisco denota el error rms cuando el número de términos K en la serie de Fourier es igual a 99.

Debido a que los coeficientes de Fourier decaen más lentamente aquí que para la sinusoide rectificada de media onda, el error rms no disminuye rápidamente. Dicho de otra manera, el espectro de onda cuadrada contiene más potencia a frecuencias más altas que la sinusoide rectificada de media onda. Esta diferencia entre las dos series de Fourier resulta porque los coeficientes de Fourier de la sinusoide rectificada de media onda son proporcionales a 1/k ² mientras que los de la onda cuadrada son proporcionales a 1/k. Si el hecho, después de 99 términos de la aproximación de la onda cuadrada, el error es mayor que 10 términos de la aproximación para la sinusoide rectificada de media onda. Los matemáticos han demostrado que ninguna señal tiene un error de aproximación rms que decae más lentamente que para la onda cuadrada.

Ejercicio\(\PageIndex{1}\)

Calcular la distorsión armónica para la onda cuadrada.

Solución

La distorsión armónica total en la onda cuadrada es:

\[1-\frac{1}{2}(\frac{4}{\pi })^{2}=20\% \nonumber \]

Más que solo decayendo lentamente, la aproximación de la serie de Fourier mostrada en la Figura 4.5.4 exhibe un comportamiento interesante.

Figura 4.5.4 Aproximación de series de Fourier a sq (t). El número de términos en la suma de Fourier se indica en cada gráfica, y la onda cuadrada se muestra como una línea discontinua en dos periodos.

Aunque la serie de Fourier de la onda cuadrada requiere más términos para una precisión de representación dada, al comparar gráficas no está claro que las dos sean iguales. ¿La serie de Fourier es realmente igual a la onda cuadrada en todos los valores de

Considera esta pregunta matemática de manera intuitiva: ¿Puede una función discontinua, como la onda cuadrada, expresarse como una suma, incluso infinita, de señales continuas? Uno debe por lo menos sospechar, y de hecho, no se puede expresar así. Este número trajo muchas críticas a Fourier por parte de la Academia Francesa de Ciencias (Laplace, Lagrange, Monge y LaCreix conformaron el comité de revisión) durante varios años después de su presentación en 1807. No se resolvió desde hace casi un siglo, y su resolución es interesante e importante de entender desde un punto de vista práctico.

Los picos extraños en la serie de Fourier de la onda cuadrada nunca desaparecen; se denominan fenómeno de Gibb después del físico estadounidense Josiah Willard Gibbs. Se producen siempre que la señal es discontinua, y siempre estarán presentes siempre que la señal tenga saltos.

Volvamos a la cuestión de la igualdad; ¿cómo puede justificarse el signo igual en la definición de la serie de Fourier? La respuesta parcial es que la igualdad puntual —todos y cada uno de los valores de t — no está garantizada. Sin embargo, los matemáticos posteriores en el siglo XIX demostraron que el error rms de la serie de Fourier siempre fue cero.

\[\lim_{k \to\infty }rms(\varepsilon _{K})=0 \nonumber \]

Lo que esto significa es que el error entre una señal y su aproximación de la serie de Fourier puede no ser cero, ¡sino que su valor rms será cero! Es a través de los ojos del valor rms que redefinimos la igualdad: La definición habitual de igualdad se llama igualdad puntual: Se dice que dos señales s ₁ (t), s ₂ (t) son iguales puntualmente si:

\[s_{1}(t)=s_{2}(t) \nonumber \]

para todos los valores de t. Una nueva definición de igualdad es la igualdad medio-cuadrada: Se dice que dos señales son iguales en el cuadrado medio si:

\[rms(s_{1}-s_{2})=0 \nonumber \]

Para las series de Fourier, los picos del fenómeno de Gibb tienen altura finita y ancho cero. El error difiere de cero solo en puntos aislados, siempre que la señal periódica contenga discontinuidades, y equivale a aproximadamente 9% del tamaño de la discontinuidad. El valor de una función en un conjunto finito de puntos no afecta su integral. Este efecto subyace a la razón por la que definir el valor de una función discontinua, como nos abstuvimos de hacer al definir la función de paso, en su discontinuidad no tiene sentido. Cualquier cosa que elija para un valor no tiene relevancia práctica ni para el espectro de la señal ni para la forma en que un sistema responde a la señal. El valor de la serie de Fourier “a” la discontinuidad es el promedio de los valores a cada lado del salto.