5.3: Grupos más adimensionales

El mayor cambio en el análisis dimensional viene con un segundo grupo adimensional independiente. Con un solo grupo adimensional, la afirmación más general que pudo hacer el universo fue

\[\textrm{dimensionless group} \sim 1\]

Con un segundo grupo, el universo gana libertad en el lado derecho:

\[\textrm{group 1} = f (\textrm{group 2})\]

donde f es una función adimensional: Toma un número adimensional como entrada, y produce un número adimensional como su salida.

Como ejemplo de dos grupos adimensionales independientes, extendamos el análisis del Problema 5.10, donde predijo la velocidad de impacto de una roca que cayó desde una altura. La velocidad de impacto depende de g y, por lo que una elección razonable para el grupo adimensional independiente es\(v \sqrt{gh}\) Por lo tanto, su valor es una constante universal, adimensional (que resulta ser\(\sqrt{2}\)). Para hacer un segundo grupo adimensional independiente, agregamos un grado de libertad al problema: que la roca se arroje hacia abajo con velocidad v ₀ (el problema anterior es el caso v ₀ =0).

Con esta complicación, ¿qué son los grupos adimensionales independientes?

Agregar una cantidad pero ninguna nueva dimensión independiente crea un grupo adimensional independiente más. Por lo tanto, hay dos grupos independientes—por ejemplo\(v/\sqrt{gh}\) y\(v_{0}/\sqrt{gh}\). La declaración adimensional más general, que tiene la forma grupo 1 = f (grupo 2), es

\[\frac{v}{\sqrt{gh}} = f(\frac{v_{0}}{\sqrt{gh}}).\]

Este punto es lo que nos puede llevar el análisis dimensional. Para ir más allá se requiere agregar conocimientos de física (Problema\(\PageIndex{1}\)). Pero el análisis dimensional ya nos dice que esta función f es una función universal: Describe la velocidad de impacto de cada objeto lanzado en el universo, sin importar la velocidad de lanzamiento, la altura de caída o la intensidad del campo gravitacional.

Ejercicio\(\PageIndex{1}\): Impact speed of a thrown rock

Para una roca arrojada hacia abajo con velocidad v ₀, utilice la conservación de energía para encontrar la forma de la función adimensional f in\(v/\sqrt{gh} = f(v_{0}/\sqrt{gh}).\)

Ejercicio\(\PageIndex{2}\): Nonideal spring

Imagínese una masa conectada a un resorte con ley de fuerza\(F \: \propto \: x^{3}\) (en lugar de la fuerza ideal-resorte\(F \: \propto \: x\)) y por lo tanto con energía potencial\(V \sim cx^{4}\) (donde C es una constante). ¿Qué curva muestra cómo el periodo de oscilación del sistema T depende de la amplitud x ₀?

Ejercicio\(\PageIndex{3}\): Rolling down the plane

En este problema, se utiliza el análisis dimensional para simplificar la búsqueda de la aceleración de un anillo rodante (sin deslizarse) hacia abajo de un plano inclinado.

a. Enumerar las cantidades de las que depende la aceleración del anillo. Pista: Incluye el momento de inercia del anillo y su radio. ¿También necesitas incluir su masa?

b. Formar grupos adimensionales independientes para escribir la declaración adimensional

\[\textrm{group proportional to } a = f (\textrm{groups not containing } a)\]

c. ¿Un anillo más grande rueda más rápido que un anillo más pequeño?

d. ¿Un anillo más denso rueda más rápido que un anillo menos denso (del mismo radio)?

5.3.1 Flexión de luz estelar por el Sol

Nuestro siguiente ejemplo de dos grupos adimensionales independientes —la desviación de la luz estelar por el Sol— ilustrará cómo incorporar el conocimiento físico en los resultados matemáticos del análisis dimensional.

Rocas, pájaros y personas sienten el efecto de la gravedad. Entonces, ¿por qué no la luz? El análisis de su desviación es un triunfo de la teoría de la relatividad general de Einstein. Sin embargo, la teoría se basa en diez ecuaciones acopladas, no lineales parcial-diferenciales. En lugar de resolver estas difíciles ecuaciones, usemos el análisis dimensional.

Debido a que este problema es más complicado que los ejemplos anteriores, organicemos la complejidad haciendo explícitos los pasos, incluyendo el paso de incorporar el conocimiento físico. ¡Divide y conquista!

1. Enumerar las cantidades relevantes.

2. Formar grupos adimensionales independientes.

3. Utilice los grupos para hacer la declaración más general sobre la desviación.

4. Reduzca las posibilidades incorporando el conocimiento físico.

Paso 1: Listado de cantidades relevantes

En el primer paso, pensamos y enumeramos las cantidades que determinan la flexión. Para encontrarlos, a menudo dibujo un diagrama con etiquetas verbales pero sin etiquetas cuantitativas. A medida que el diagrama clama por etiquetas cuantitativas, sugiere cantidades para la lista.

El camino doblado significa que la estrella desplaza su posición aparente. El cambio se mide de manera más natural no como una distancia absoluta sino como un ángulo\(\theta\). Por ejemplo, si\(\theta\) = 180 ^° (\(\pi\)radianes), mucho más grande que la desviación probable, la estrella se desplazaría a la mitad del cielo.

\(\theta\)	1	ángulo
Gm	L ^3 T ^-2	La gravedad del sol
r	L	enfoque más cercano

Las etiquetas y la lista deben incluir nuestro objetivo, que es el ángulo de deflexión\(\theta\). Debido a que la deflexión es producida por la gravedad, también deberíamos incluir la constante gravitacional de Newton G y la masa del Sol m (usaremos el símbolo más general m en lugar de M _Sol, porque podemos aplicar la fórmula a caminos de luz alrededor de otras estelares objetos). Estas cantidades podrían unirse a la lista como dos cantidades separadas. Sin embargo, las consecuencias físicas de la gravedad —por ejemplo, la fuerza gravitacional— dependen de G y m solo a través del producto Gm. Por lo tanto, incluyamos solo la abstracción de Gm en la lista. (Problema 5.19 te muestra cómo encontrar sus dimensiones.)

La cantidad final en la lista se basa en nuestro conocimiento de que la gravedad se debilita con la distancia. Por lo tanto, incluimos la distancia desde el Sol hasta el haz de luz. La frase “distancia del Sol” es ambigua, porque el haz se encuentra a diversas distancias. Nuestra cantidad r será la distancia más corta desde el centro del Sol hasta el haz (la distancia de aproximación más cercana).

Ejercicio\(\PageIndex{4}\): Dimensions of Gm and G

Utilice la ley de la gravitación universal de Newton,\(F = Gm_{1}m_{2}/r^{2}\), para encontrar las dimensiones de Gm y G.

Paso 2: Formar grupos adimensionales independientes

El segundo paso es formar grupos adimensionales independientes. Un grupo es fácil: El ángulo ya\(\theta\) es adimensional. Desafortunadamente, tres cantidades y dos dimensiones independientes (L y T) producen solo un grupo adimensional independiente. Con un solo grupo adimensional, la afirmación más general es meramente\(\theta\) = constante.

Esta predicción es absurda. La flexión, si se produce por gravedad, tiene que depender de Gm y r. Estas cantidades tienen que aparecer en un segundo grupo adimensional. Crear un segundo grupo, sabemos por el teorema de Buckingham Pi, requiere al menos una cantidad más. Su ausencia indica que a nuestro análisis le falta una física esencial.

¿Qué física le falta?

Ninguna cantidad hasta ahora distingue entre el camino de la luz y de, digamos, un planeta. Una diferencia crucial es que la luz viaja mucho más rápido que un planeta. Representemos esta importante característica de la luz al incluir el c.

\(\theta\)	1	ángulo
Gm	L ^3 T ^-2	La gravedad del sol
r	L	enfoque más cercano
c	LT ^-1	velocidad de la luz

Esta cantidad, una velocidad, no introduce una nueva dimensión independiente (utiliza longitud y tiempo). Por lo tanto, aumenta el número de grupos adimensionales independientes en uno, de uno a dos. Para encontrar el nuevo grupo, primero verifique si alguna dimensión aparece en sólo dos cantidades. Si lo hace, la búsqueda se simplifica. El tiempo aparece solo en dos cantidades: en Gm como T ⁻² y en c como T ⁻¹. Para cancelar el tiempo de espera, el nuevo grupo adimensional debe contener Gm/c ². Este cociente contiene una potencia de longitud, por lo que nuestro grupo adimensional es Gm/rc ².

Como esperábamos, el nuevo grupo contiene Gm y r. Su forma ilustra nuevamente que las cantidades con dimensiones no son significativas por sí solas. Por saber solo Gm no es suficiente para decidir si la gravedad es fuerte o no. Como cantidad con dimensiones, Gm debe compararse con otra cantidad relevante con las mismas dimensiones. Aquí, esa cantidad es rc ², y la comparación lleva a la relación adimensional Gm/rc ².

¿Podemos elegir otros pares de grupos adimensionales independientes?

Sí. Por ejemplo,\(\theta\) y\(Gm \theta /rc^{2}\) también hacer un conjunto de grupos adimensionales independientes. Matemáticamente, todos los pares de grupos adimensionales independientes son equivalentes, ya que cualquier par puede representar cualquier declaración cuantitativa sobre la flexión de la luz.

No obstante, mira hacia el objetivo: Esperamos resolver para θ. Si θ aparece en ambos grupos, terminaremos con una ecuación implícita para θ, donde θ aparece en ambos lados del signo igual. Aunque tal ecuación es matemáticamente legítima, es mucho más difícil pensar y resolver que una ecuación explícita, donde θ está solo del lado izquierdo.

Por lo tanto, al elegir grupos adimensionales independientes, coloque la cantidad objetivo en un solo grupo. Esta regla general no quita toda nuestra libertad en la elección de los grupos, sino que limita en gran medida las elecciones.

Ejercicio\(\PageIndex{5}\): Physical interpretation of the new group

Interpreta el grupo adimensional Gm/rc ² multiplicando por m _luz/m _luz y reagrupando las cantidades hasta encontrar interpretaciones físicas para el numerador y denominador.

Paso 3: Hacer la declaración adimensional más general

El tercer paso es usar los grupos adimensionales independientes para escribir la declaración más general sobre el ángulo de flexión. Tiene la forma grupo 1 = f (grupo 2). Aquí,

\[\theta= f (\frac{gm}{rc^{2}}),\]

donde f es una función universal, adimensional. El análisis dimensional no puede determinar f. No obstante, nos ha dicho que f es una función únicamente de Gm/rc ² y no de las cuatro cantidades G, m, r y c por separado. Esa información es la gran simplificación.

Paso 4: Utilizar el conocimiento físico para reducir las posibilidades El espacio de posibles funciones —aquí, todas las funciones no patológicas de una variable— es vasto. Por lo tanto, el cuarto y último paso es estrechar las posibilidades de f incorporando el conocimiento físico. Primero, imagina aumentar el efecto de la gravedad al aumentar la masa m —lo que aumenta Gm/rc ².

Este cambio debería, basado en nuestra intuición física sobre la gravedad, aumentar también el ángulo de flexión. Por lo tanto, f debe ser una función monótonamente creciente de Gm/rc ². Segundo, imagina un mundo antigravedad, donde la constante gravitacional G es negativa. Entonces el Sol desviaría la luz lejos de él, haciendo negativo el ángulo de flexión. En términos de\(x \equiv Gm/rc^{2}\), esta restricción elimina incluso funciones de x, tales como\(f(x) \sim x^{2}\), que producen el mismo signo para el ángulo de flexión independiente del signo de x.

La función más simple que cumple con las restricciones de monotonicidad y signo es f (x) ~ x. En términos del segundo grupo GM/rc ², la forma f (x) ~ x es la declaración adimensional sobre la flexión

\[\theta \sim \frac{GM}{rc^{2}}.\]

Todas las teorías razonables de la gravedad predecirán esta relación, porque es casi en su totalidad un requisito matemático. Las teorías difieren solo en el factor adimensional oculto en el signo de aproximación simple ~:

\[\theta = \frac{Gm}{rc^{2}} \times \left \{ \begin{array} {ll} 1 \: \textrm{(simplest guess);} \\ 2 \: \textrm{(Newtonian gravity);} \\ 4 \: \textrm{(general relativity).} \end{array} \right. \]

El factor de 2 para la gravedad newtoniana resulta de resolver la trayectoria de una roca que pasa por el Sol con velocidad c. El factor de 4 para generalrelatividad, el doble del valor newtoniano, resulta de resolver las diez ecuaciones parcial-diferenciales en el límite de que el campo gravitacional es débil.

¿Qué tan grandes son estos ángulos?

Primero calculemos los ángulos de flexión más cercanos al hogar, producidos por la gravedad de la Tierra. Para un rayo de luz simplemente pastando la superficie de la Tierra, el ángulo de flexión (¡en radianes!) es aproximadamente 10 ⁻⁹:

\[\theta_{Earth} \sim \frac{\overbrace{6 \times 10^{-11} \textrm{kg}^{-1} \textrm{ m}^{3} \textrm{ s}^{-2}}^{G} \times \overbrace{6 \times 10^{24}}^{m_{Earth}}}{\underbrace{6.4 \times 10^{6} \textrm{m}}_{R_{Earth}} \times \underbrace{10^{17} \textrm{m}^{2} \textrm{s}^{-2}}_{c^{2}}} \approx 0.7 \times 10^{-9}.\]

¿Podemos observar este ángulo?

El ángulo de flexión es el desplazamiento angular en la posición de la estrella haciendo la luz de las estrellas. Para observar estos cambios, los astrónomos comparan una imagen telescópica de la estrella y el cielo circundante, con y sin la desviación. Un telescopio con lente de diámetro D puede resolver ángulos aproximadamente tan pequeños como\(\lambda /D\), donde\(\lambda\) está la longitud de onda de la luz. Como resultado, una lente que puede resolver 0.7 ×10 ⁻⁹ radianes tiene un diámetro de al menos 700 metros:

\[D \sim \frac{\lambda}{\theta_{Earth}} \sim \frac{0.5 \times 10^{-6} m}{0.7 \times 10^{-9}} \approx 700 m.\]

Por sí solo, esta longitud no significa mucho. Sin embargo, la lente telescópica más grande tiene un diámetro de aproximadamente 1 metro; el espejo telescópico más grande, en un diseño de telescopio diferente, sigue siendo de solo 10 metros. Ninguna lente práctica o espejo puede tener 700 metros de diámetro. Así, no hay manera de ver la desviación producida por el campo gravitacional de la Tierra.

Por lo tanto, los físicos buscaron una fuente más fuerte de flexión de la luz. El ángulo de flexión es proporcional a m/r. La mayor masa en el sistema solar es el Sol. Para un rayo de luz que roza la superficie del Sol, r = R _Sol y m = M _Sol. Entonces, la relación de ángulos de flexión producidos por el Sol a la Tierra es

\[\frac{\theta_{Sun}}{\theta_{Earth}} = \frac{M_{Sun}}{m_{Earth}} \times (\frac{R_{sun}}{R_{Earth}})^{-1}.\]

La relación de masa es aproximadamente 3×10 ⁵; la relación de radio es aproximadamente 100. Por lo tanto, la relación de ángulos de deflexión es aproximadamente 3000. El diámetro requerido de la lente, que es inversamente proporcional a\(\theta\), es correspondientemente menor de 700 metros por un factor de 3000: aproximadamente 25 centímetros o 10 pulgadas. Ese tamaño de lente es plausible, y la desviación podría ser medible.

Entre 1909 y 1916, Einstein creía que una teoría correcta de la gravedad predeciría el valor newtoniano de 4.2×10 ⁻⁶ radianes o 0.87 segundos de arco:

\[\underbrace{0.7 \times 10^{-9} \textrm{rad}}_{\sim \theta_{Earth}} \times \underbrace{2}_{\textrm{Newtonian gravity}} \times \underbrace{3000}_{\theta_{Sun}/\theta_{Earth}} \sim 4.2 \times 10^{-6} \textrm{ rad}.\]

El astrónomo alemán Soldner había derivado el mismo resultado en 1803. Las expediciones del eclipse para poner a prueba su predicción (y la de Soldner) llovieron o se nublaron. Para cuando una expedición tuvo suerte con el clima, en 1919, Einstein había inventado una nueva teoría de la gravedad, la relatividad general, y predijo una desviación del doble de grande, o 1.75 segundos de arco.

La expedición de eclipse de 1919, dirigida por Arthur Eddington de la Universidad de Cambridge y usando una lente de 13 pulgadas, midió la deflexión. Las mediciones son difíciles y los resultados no fueron lo suficientemente precisos como para decidir claramente qué teoría era la correcta. Pero 1919 fue el primer año después de la Primera Guerra Mundial, en la que Alemania y Gran Bretaña habían luchado entre sí casi hasta el olvido. Una teoría inventada por un alemán, confirmada por un inglés (de la universidad de Newton, nada menos) —tal imagen fue bienvenida después de la guerra. La prensa mundial y la comunidad científica declararon vindicado a Einstein.

Una confirmación adecuada de la predicción de Einstein llegó solo con el advenimiento de la radioastronomía, que permitió medir con precisión pequeñas deflexiones (Problema 5.21). Los resultados, descritos como el factor adimensional multiplicando Gm/rc ², fueron alrededor de 4 ± 0.2, definitivamente diferentes de la predicción newtoniana de 2 y consistentes con la relatividad general.

Ejercicio\(\PageIndex{6}\): Accuracy of radio telescope measurements

La resolución angular de un telescopio es\(\lambda/D\), donde\(\lambda\) está la longitud de onda y D es el diámetro del telescopio. Pero las ondas de radio tienen una longitud de onda mucho más larga que la luz. ¿Cómo pueden ser mucho más precisas las mediciones del ángulo de flexión que se realizan con radiotelescopios que las mediciones realizadas con telescopios ópticos?

Ejercicio\(\PageIndex{7}\): Another theory of gravity

Una alternativa a la gravedad newtoniana y a la relatividad general es la teoría de la gravitación Brans—Dicke [3]. Busca lo que predice para el ángulo que el Sol desviaría la luz estelar. Exprese su respuesta como el prefactor adimensional en\(\theta \sim Gm/rc^{2}\).

5.3.2 Arrastre

Aún más difíciles que las ecuaciones de relatividad general, que al menos han sido resueltas por problemas realistas, son las ecuaciones Navier—Stokes de mecánica de fluidos. Los conocimos por primera vez en la Sección 3.5, donde su complejidad nos empujó a encontrar una alternativa para resolverlos directamente. Se utilizó un argumento de conservación, el cual probamos usando un cono descendente, y concluimos que la fuerza de arrastre sobre un objeto que viaja a través de un fluido es

\[F_{drag} \sim \rho v^{2}A_{cs},\]

donde\(\rho\) es la densidad del fluido, v es la velocidad del objeto, y A _cs es su área de sección transversal. Este resultado es el punto de partida para nuestro análisis dimensional.

Con el _arrastre F dependiente de\(\rho\), v y A _cs, hay cuatro cantidades y tres dimensiones independientes. Por lo tanto, por el teorema de Buckingham Pi, existe un grupo adimensional independiente. Nuestra expresión para la fuerza de arrastre ya da a uno de esos grupos

\[\frac{F_{drag}}{\rho v^{2}A_{cs}}.\]

Debido a que el\(\rho v^{2}\) en el denominador parece mv ² en energía cinética, tradicionalmente se incluye en el denominador un factor de la mitad:

\[\textrm{group 1} \equiv \frac{F_{drag}}{\frac{1}{2} \rho v^{2} A_{cs}}.\]

El grupo adimensional resultante se denomina coeficiente de arrastre c _d.

\[c_{d} \equiv \frac{F_{drag}}{\frac{1}{2} \rho v^{2} A_{cs}}\]

Como único grupo adimensional, tiene que ser una constante: No hay otro grupo del que pueda depender. Por lo tanto,

\[\frac{F_{drag}}{\frac{1}{2} \rho v^{2} A_{cs}} = \textrm{dimensionless constant}.\]

Este resultado es equivalente a nuestra predicción basada en la conservación de la energía, eso\(F_{drag} \sim \rho v^{2} A_{cs}\). Sin embargo, los problemas ocurren cuando nos preguntamos sobre el valor de la constante adimensional.

El análisis dimensional, como técnica matemática, no puede predecir la constante. Hacerlo requiere de un razonamiento físico, que inicia con la observación de que el arrastre consume energía. Aquí, ninguna cantidad de la que _{dependa el arrastre} F, es decir\(rho\), v o A _cs, representa un mecanismo de pérdida de energía. Por lo tanto, el coeficiente de arrastre debe ser cero. Si bien este valor es consistente con la predicción de que el coeficiente de arrastre es constante, ¡contradice toda nuestra experiencia de fluidos!

Nuestro análisis necesita incluir un mecanismo de pérdida de energía. En los fluidos, la pérdida se debe a la viscosidad (para un objeto que se mueve a una velocidad constante y no genera ondas). Su física es el tema de la Sección 7.3.2, como ejemplo de una constante de difusión. Para nuestros propósitos aquí, necesitamos solo sus dimensiones para incorporar la viscosidad a un grupo adimensional: Las dimensiones de la viscosidad cinemática\(\nu\) son L ² T ⁻¹. (Desafortunadamente, en casi todas las fuentes, los símbolos estándar para velocidad y viscosidad cinemática,\(v\) y \(\nu\), parecen similares; sin embargo, aún más confusión resultaría de seleccionar nuevos símbolos).

Así, la viscosidad cinemática se une a nuestra lista. Agregar una cantidad sin agregar una nueva cota independiente crea un nuevo grupo adimensional independiente. De igual manera, en nuestro análisis de la desviación de la luz estelar (Sección), al agregar la velocidad de la luz c se creó un segundo grupo adimensional independiente.

¿Cuál es este nuevo grupo que contiene viscosidad?

Antes de encontrar al grupo, mira hacia adelante cómo se va a utilizar. Con un segundo grupo, la declaración más general tiene la forma

\[\underbrace{\textrm{group 1}}_{c_{d}} = f(\textrm{group 2}).\]

Nuestro objetivo es F _drag, que ya forma parte del grupo 1. Incluir F _drag también en el grupo 2 sería una mala táctica, ya que produciría una ecuación con F _drag en ambos lados y, adicionalmente, envuelto en el lado derecho en la función desconocida f. Mantener F _drag fuera del grupo 2.

\(v\)	LT ^-1	velocidad
A cs	L ^2	zona
\(rho\)	ML ^-3	densidad de fluidos
\(\nu\)	L2T ^-1	viscosidad

Para hacer este grupo a partir de las otras cantidades\(v\), A _cs\(\rho\), y\(\nu\), buscar dimensiones que aparecen en solo una o dos cantidades. La masa aparece solo en la densidad; así, la densidad no puede aparecer en el grupo 2: Si fuera parte del grupo 2, no habría forma de cancelar las dimensiones de la masa, y el grupo 2 no podría ser adimensional.

El tiempo aparece en dos cantidades: velocidad\(v\) y viscosidad\(\nu\). Debido a que cada cantidad contiene la misma potencia de tiempo (T ⁻¹), el grupo 2 tiene que contener el cociente\(v\)/\(\nu\)—de lo contrario las dimensiones del tiempo no se cancelarían.

Esto es lo que sabemos hasta ahora de este grupo adimensional: Para que esa masa desaparezca, no pueda contener la denisty\(\rho\); para que el tiempo desaparezca, debe contiarse\(v\) y\(\nu\) como su cociente\(v/\nu\). La tarea restante es hacer desaparecer la longitud, para lo cual usamos el área transversal del objeto A _cs. El cociente\(v/\nu\) tiene dimensiones de L ^-1, por lo que\(\sqrt{A_{cs}}v/\nu\) es un nuevo grupo adimensional independiente.

En lugar de\(\sqrt{A_{cs}}\), por lo general se usa el diámetro D. Con esa elección, nuestro grupo 2 se llama el número Reynolds Re.

\[\textrm{Re} \equiv \frac{vD}{\nu}.\]

La conclusión del análisis dimensional es entonces

\[\underbrace{\textrm{drag coefficient}}_{c_{d}} = \underbrace{f(\textrm{Reynolds number}).}_{\textrm{Re}}\]

Para cada forma, la función adimensional f es una función universal; depende de la forma del objeto, pero no de su tamaño. Por ejemplo, una esfera, un cilindro y un cono tienen diferentes funciones f _esfera, f _cilindro y f _cono. De manera similar, un cono de ángulo estrecho y un cono de gran angular tienen diferentes funciones.

Pero una esfera pequeña y otra grande se describen con la misma función, como lo son un cono grande y uno pequeño del mismo ángulo de apertura. Cualquier diferencia en los coeficientes de arrastre para objetos de diferentes tamaños de la misma forma resulta solo de la diferencia en los números de Reynolds (diferente porque los tamaños son diferentes).

Aquí vemos el poder del análisis dimensional. Nos muestra que al universo no le importa el tamaño, la velocidad o la viscosidad individualmente. El universo se preocupa por ellos sólo a través de la abstracción conocida como el número de Reynolds. Es la única información necesaria para determinar el coeficiente de arrastre (para una forma dada).

Ahora usemos este marco adimensional para analizar el experimento del cono: Los datos experimentales mostraron que los conos pequeños y grandes cayeron a la misma velocidad, aproximadamente 1 metro por segundo.

¿Cuáles son los números de Reynolds correspondientes?

El cono pequeño tiene un diámetro de 0.75×7 centímetros (0.75 porque se eliminó una cuarta parte de la circunferencia original), que es aproximadamente 5.3 centímetros. La viscosidad del aire es aproximadamente 1.5×10 ⁻⁵ metros cuadrados por segundo (estimación que haremos en la Sección 7.3.2). El número resultante de Reynolds es aproximadamente 3500:

\[\textrm{RE} = \frac{\overbrace{1 \textrm{ m s}^{-1}}^{v} \times \overbrace{0.053 \textrm{ m}}^{D}}{\underbrace{1.5 \times 10^{-5} \textrm{ m}^{2} \textrm{ s}^{-1}}_{v}} \approx 3500.\]

¿Cuál es el número de Reynolds para el cono grande?

Nunca hagas un cálculo desde cero cuando puedas usar el razonamiento proporcional. Ambos conos experimentan la misma viscosidad y comparten la misma velocidad de caída. Por lo tanto, podemos\(v\) considerar\(\nu\) y ser constantes, dejando el número de Reynolds\(vD/\nu\) proporcional justo al diámetro D.

Debido a que el cono grande tiene el doble de diámetro que el cono pequeño, tiene el doble del número de Reynolds:

\[\textrm{RE}_{\textrm{large}} = 2 \times \textrm{Re}_{\textrm{small}} \approx 7000.\]

En ese número de Reynolds, ¿cuál es el coeficiente de arrastre del cono?

El coeficiente de arrastre es

\[c_{d} \equiv \frac{F_{drag}}{\frac{1}{2} \rho_{air} v^{2} A_{cs}}\]

El cono cae a su velocidad terminal, por lo que la fuerza de arrastre también es su peso W:

\[F_{drag} = W = A_{paper}\sigma_{paper}g,\]

donde\(\sigma_{paper}\) es la densidad de área (masa por área) del papel y Un _papel es el área de la plantilla de cono. El coeficiente de arrastre es entonces

\[c_{d} = \frac{\overbrace{A_{paper} \sigma_{paper} g}^{F_{drag}}}{\frac{1}{2} \rho_{air} A_{cs} v^{2}}.\]

Como lo demostramos en la Sección 3.5.2,

\[A_{cs} = \frac{3}{4} A_{paper}.\]

Esta proporcionalidad significa que las áreas cancelan fuera del coeficiente de arrastre:

\[c_{d} = \frac{\sigma_{paper}g}{\frac{1}{2} \rho_{air} \times \frac{3}{4} v^{2}}.\]

Para calcular c _d, conecte la densidad de área\(\sigma_{paper} \approx 80\) gramos por metro cuadrado y el medidor de velocidad\(v \approx 1\) medido por segundo:

\[c_{d} \approx \frac{\overbrace{8 \times 10^{-2} \textrm{ kg m}^{-2}}^{\sigma_{paper}} \times \overbrace{10 \textrm{ m s}^{-2}}^{g}}{\frac{1}{2} \times \underbrace{1.2 \textrm{ kg m}^{-3}}_{\rho_{air}} \times \frac{3}{4} \times \underbrace{1 \textrm{ m}^{2} \textrm{ s}^{-2}}_{v^{2}}} \approx 1.8.\]

Debido a que ninguna cantidad en este cálculo depende del tamaño del cono, ambos conos tienen el mismo coeficiente de arrastre. (Nuestro coeficiente de arrastre estimado es significativamente mayor que el coeficiente de arrastre canónico para un cono sólido, aproximadamente 0.7, y es aproximadamente el coeficiente de arrastre para una cuña).

Así, el coeficiente de arrastre es independiente del número de Reynolds, al menos, para números de Reynolds entre 3500 y 7000. El experimento de cono gigante del Problema 4.16 muestra que la independencia se mantiene incluso a Re ∼ 14 000. Dentro de este rango, la función adimensional f in

\[\textrm{drag coefficient} = f_{cone}\textrm{(Reynolds number)}\]

es una constante. ¡Qué simple descripción de la complejidad del flujo de fluidos!

Esta conclusión para el _cono f es válida para la mayoría de las formas. Los datos de arrastre más extensos son para una esfera-trazada a continuación en ejes log-log (datos adaptados de Fluid-Dynamic Drag: Información práctica sobre arrastre aerodinámico y resistencia hidrodinámica [23]):

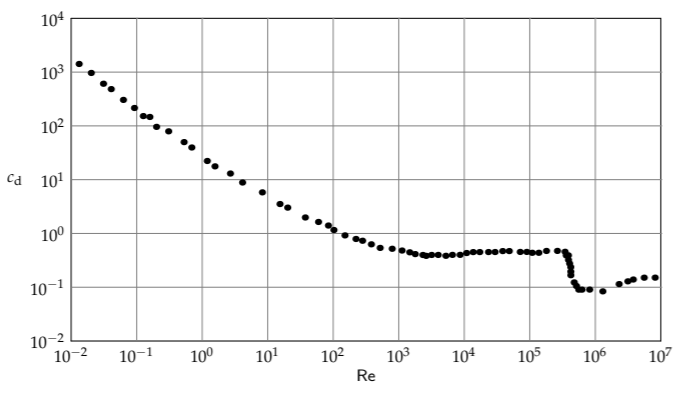
Al igual que el coeficiente de arrastre para el cono, el coeficiente de arrastre para una esfera es casi constante ya que el número de Reynolds varía de 3500 a 7000. El coeficiente de arrastre se mantiene constante incluso en todo el rango más amplio 2000... 3 × 10 ⁵. Alrededor de Re ≈ 3 × 10 ⁵, el coeficiente de arrastre cae en un factor de 5, de 0.5 a aproximadamente 0.1. Esta caída es la razón por la que las pelotas de ggolf tienen hoyuelos (explicarás la conexión en Problema 7.24).

A números bajos de Reynolds, el coeficiente de arrastre se vuelve grande. Este comportamiento, que representa un pequeño objeto que rezuma a través de la miel, se explicará en la Sección 8.3.1.2 utilizando la herramienta de casos fáciles. El punto principal aquí es que, para la mayoría de los flujos cotidianos, donde el número de Reynolds se encuentra en el rango de “pocos miles a pocos cientos de miles”, el coeficiente de arrastre es una constante que depende únicamente de la forma del objeto.

Ejercicio\(\PageIndex{8}\): Giant cone

¿Qué tan grande, medido por el diámetro de su sección transversal, tendría que ser un cono de papel para que su caída tuviera un número de Reynolds de aproximadamente 3 × 10 ⁵ (el número de Reynolds al que cae significativamente el coeficiente de arrastre de una esfera)?

Ejercicio\(\PageIndex{9}\): Reynolds numbers

Estimar el número de Reynolds para (a) una gota de lluvia que cae, (b) un mosquito volador, (c) una persona caminando y (d) un jet jumbo volando a su velocidad de crucero

Ejercicio\(\PageIndex{10}\): Compound pendulum

Usa el análisis dimensional para deducir todo lo que puedas sobre el período T de un péndulo compuesto, es decir, un péndulo donde el bob no es una masa puntual sino un objeto extendido de masa m. El lightrod (ya no es una cuerda) de longitud l se fija al centro de masa del objeto, el cual tiene un momento de inercia I _CM sobre el punto de unión. (Supongamos que la amplitud de oscilación es pequeña y por lo tanto no afecta al periodo.)

Ejercicio\(\PageIndex{11}\): Terminal velocity of a raindrop

En Problema 3.37, estimó la velocidad terminal de una gota de lluvia usando

\[F_{drag} \sim \rho_{air} A_{cs}v^{2}.\]

Rehacer el cálculo usando la información más precisa que c _d ≈ 0.5 y conservando el factor de 4\(\pi\) /3 en el volumen de una gota de lluvia esférica