5.4: Temperatura y cambio

Los ejemplos anteriores de análisis dimensional han sido mecánicos, utilizando las dimensiones de longitud, masa y tiempo. La temperatura y la carga también son esenciales para describir el mundo y son igualmente susceptibles de análisis dimensional. Empecemos con la temperatura.

5.4.1 Temperatura

Para manejar la temperatura, ¿necesitamos agregar otra dimensión fundamental?

Representar la temperatura como una nueva dimensión fundamental es un método, y la dimensión está simbolizada por\(\Theta\). Sin embargo, hay un método más sencillo. Utiliza otra constante fundamental de la naturaleza: la constante k _B de Boltzmann. Tiene dimensiones de energía por temperatura; así, conecta la temperatura con la energía. En unidades SI, k _B es aproximadamente 1.6 × 10 ⁻²³ julios por kelvin. Cuando aparezca una temperatura T, conviértala a la energía correspondiente k _B T (así como convertimos G, en problemas de gravedad, a G _m).

Para nuestro primer ejemplo de temperatura, calculemos la velocidad de las moléculas de aire. Entonces usaremos ese conocimiento para estimar la velocidad del sonido. Debido a que la velocidad\(v\) de las moléculas de aire es resultado de la energía térmica, depende de k _B T. Pero\(v\) y k _B T —dos cantidades hechas de dos dimensiones independientes— no pueden formar un grupo adimensional. Necesitamos una cantidad más: la masa m de una molécula de aire.

Aunque estas tres cantidades contienen tres dimensiones, solo dos de las dimensiones son independientes, por ejemplo, M y LT ⁻¹. Por lo tanto, las tres cantidades producen un grupo adimensional independiente. Una opción razonable para ello es\(mv^{2}/k_{B}T\). Entonces

\(v\)	LT ^-1	velocidad térmica
\(k_{B}T\)	ML ^2 T ^-2	energía térmica
\(m\)	M	masa molecular

Este resultado es bastante exacto. El prefactor adimensional faltante es\(\sqrt{3}\) para la velocidad cuadrática media y\(\sqrt{8/\pi}\) para la velocidad media.

El resultado del análisis dimensional ayuda a predecir la velocidad del sonido. En un gas, el sonido viaja debido a la presión, que es resultado del movimiento térmico. Por lo tanto, es plausible que la velocidad del sonido c _s sea comparable a la velocidad térmica. Entonces,

\[c_{s} \sim \sqrt{\frac{k_{B}T}{m}}.\]

Para evaluar la velocidad numéricamente, multiplique por una forma de 1 basado en el número de Avogadro:

\[c_{s} \sim \sqrt{\frac{k_{B}T}{m} \times \frac{N_{A}}{N_{A}}}.\]

El numerador ahora contiene\(k_{B}N_{A}\), que es la constante de gas universal R:

\[R \approx \frac{8J}{mol K}.\]

El denominador en la raíz cuadrada es\(mN_{A}\): la masa de una molécula multiplicada por el número de Avogadro. Por lo tanto, es la masa de un mol de moléculas de aire. El aire es principalmente N ₂, con una masa atómica de 28. Incluyendo el oxígeno para nosotros los animales, la masa molar de aire es de aproximadamente 30 gramos por mol. El enchufar 300K para temperatura ambiente da una velocidad térmica de aproximadamente 300 metros por segundo:

\[c_{s} \sim \sqrt{\frac{8J mol^{-1}K^{-1} \times 300K}{3 \times 10^{-2}kg mol^{-1}}} \approx 300 m s^{-1}.\]

La velocidad real del sonido es de 340 metros por segundo, no muy lejos de nuestra estimación basada en análisis dimensional y un poco de razonamiento físico. (La discrepancia restante se debe a la diferencia entre compresión y expansión isotérmica y adiabática. Para un efecto relacionado, luego intente Problema 8.27.)

Con esta comprensión de cómo manejar la temperatura, usemos el análisis dimensional para estimar la altura de la atmósfera. Esta altura, llamada altura de escala H, es la longitud sobre la cual cambian significativamente las propiedades de la atmósfera, como la presión y la densidad. A la altura H, la densidad atmosférica y la presión serán significativamente menores que a nivel del mar.

El primer paso en el análisis dimensional es enumerar las cantidades que determinan la altura. Esa lista requiere un modelo físico: La atmósfera es una competencia entre la gravedad y el movimiento térmico. La gravedad arrastra las moléculas hacia la Tierra; el movimiento térmico las extiende por todo el universo. Nuestra lista debe incluir cantidades que representen ambos lados de esa competencia: m y g para la gravedad, y\(k_{B}T\) para la energía térmica.

H	L	altura de la atmósfera
g	LT ^-2	gravedad
\(k_{B}T\)	ML ^-2 T ^-2	energía térmica
m	M	masa molecular

Cuatro cantidades (incluyendo la meta H) construidas a partir de tres dimensiones independientes producen un grupo adimensional independiente. Una elección razonable para el grupo —razonable porque es proporcional a la meta H — es la relación\(mgH/k_{B}T\). Por lo tanto, la altura de la escala de la atmósfera viene dada por

\[H \sim \frac{k_{B}T}{mg}\]

Para evaluar esta altura numéricamente, vuelva a convertir la constante k _B de Boltzmann a la constante de gas universal R multiplicando por\(N_{A}/N_{A}\):

\[H \sim \frac{\overbrace{k_{B}N_{A}}^{R}T}{\underbrace{mN_{A}}_{m_{molar}}g} \approx \frac{\overbrace{8 \textrm{J mol}^{-1} \textrm{K}^{-1}}^{R} \times 300K}{\underbrace{3 \times 10^{-2} \textrm{ kg mol}^{-1}}_{m_{molar}} \times 10 \textrm{ m s}^{-2}} \approx 8 \textrm{ km.}\]

Por lo tanto, a 8 kilómetros sobre el nivel del mar, la presión atmosférica y la densidad deberían ser significativamente menores que a nivel del mar. Esta conclusión es razonable: el Monte Everest tiene 9 kilómetros de altura, donde el aire significativamente más delgado requiere que los escaladores lleven tanques de oxígeno.

Como regla general para una función en descomposición como la presión atmosférica o la densidad, un “cambio significativo” puede estimarse como un aumento o, aquí, una caída por un factor de\(e\) (Para más información sobre esta regla general, intente Problema 6.36 después de haber estudiado la formación de grumos; vea también la Sección 3.2.1 de Matemáticas de lucha callejera [33].) En efecto, a 8 kilómetros, los parámetros atmosféricos estandarizados relativos al nivel del mar son\(\rho/\rho_{0} \approx 0.43\) y\(p/p_{0} \approx 0.35\). A modo de comparación,\(1/e\) es aproximadamente 0.37.

5.4.2 Carga

Nuestra segunda nueva dimensión es la carga, simbolizada por Q. Al introducir la carga, podemos aplicar el análisis dimensional a los fenómenos eléctricos. Comencemos por encontrar las dimensiones de las cantidades eléctricas

¿Cuáles son las dimensiones de corriente, voltaje y resistencia?

La corriente es el flujo de carga; tiene dimensiones de carga por tiempo. Usar I para denotar corriente y [I] para denotar sus dimensiones

\[[I] = QT^{-1}\]

Las dimensiones del voltaje se pueden determinar a partir de la relación

\[\textrm{voltage} \times \textrm{current} = \textrm{power}\]

La ecuación dimensional correspondiente es

\[[voltage] = \frac{[power]}{[current]}.\]

Debido a que las dimensiones de potencia (energía por tiempo) son ML ² T ^-3, y las dimensiones de la corriente son QT ^-1, las dimensiones de voltaje son ML ² T ^-2 Q ^-1:

\[[voltage]= \frac{ML^{2}T^{-3}}{QT^{-1}} = ML^{2}T^{-2}Q^{-1}.\]

En esta expresión, la combinación dimensional ML ² T ⁻² es energía. Por lo tanto, el voltaje también es energía por carga. Como resultado, un electrón voltio (carga de 1 electrón por 1 voltio) es una energía. Unos pocos electrón voltios es la energía en los enlaces químicos. Debido a que los enlaces químicos reflejan un cambio en uno o dos electrones, los voltajes atómicos y moleculares deben ser de unos pocos voltios. (Una consecuencia cotidiana es que las baterías típicas suministran algunos voltios).

Para encontrar las dimensiones de la resistencia, escribiremos la ley de Ohm como una ecuación dimensional:

\[[resistance] = \frac{[voltage]}{[current]} = \frac{ML^{2}T^{-2}Q^{-1}}{QT^{-1}} = ML^{2}T^{-1}Q^{-2}.\]

Para simplificar estas dimensiones, use [V] —las dimensiones del voltaje— como abstracción para el desorden dimensional ML ² T ⁻² Q ⁻¹. Entonces,

\[[resistance] = [V] \times TQ^{-1}.\]

Esta alternativa es útil cuando la entrada y salida de un circuito es voltaje. Entonces, tratar las dimensiones del voltaje como una dimensión fundamental simplifica la tarea de encontrar grupos adimensionales. (Para practicar en el uso de las dimensiones de voltaje, intente Problema\(\PageIndex{1}\).)

Ejercicio\(\PageIndex{1}\): Capacitance and inductance

Exprese las dimensiones de capacitancia e inductancia usando L, M, T y Q. Luego escríbelas usando [V] (las dimensiones del voltaje) junto con cualquier dimensión fundamental que necesite.

Ejercicio\(\PageIndex{2}\): RC circuit

En este problema, se aplica el análisis dimensional al circuito RC de paso bajo que introdujimos en la Sección 2.4.4. En particular, hacer el voltaje de entrada V _en cero para el tiempo t < 0 y un voltaje fijo V ₀ para t ≥ 0. El objetivo es la declaración adimensional más general sobre el voltaje de salida V, que depende de V ₀, t, R y C.

a. Usando [V] para representar las dimensiones de voltaje, rellene una tabla de análisis dimensional para las cantidades V, V ₀, t, R y C.

b. ¿Cuántas dimensiones independientes están contenidas en estas cinco cantidades?

c. Formar grupos adimensionales independientes y escribir la declaración más general en la forma

\[\textrm{group containing } V \textrm{ but not } t = f \textrm{(group containing } t \textrm{ but not } V, \textrm{ ...)}, \]

donde el... representa el tercer grupo adimensional (si existe). Compara tu expresión con el análisis del circuito RC en la Sección 2.4.4.

Ejercicio\(\PageIndex{3}\): Dimensional analysis of an LRC circuit

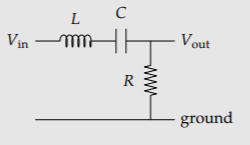
En el circuito LRC, el voltaje de entrada V _in es la parte real de una señal complejo-exponencial\(V_{0}e^{j \omega t}\), donde V ₀ es la amplitud de entrada y\(\omega\) es la frecuencia de oscilación angular. El voltaje de _salida V es entonces la parte real de\(V_{1}e^{j \omega t}\), donde V ₁ es la amplitud de salida (posiblemente compleja). ¿Qué cantidades determinan la ganancia G, definida como la relación V ₁/V ₀? ¿Cuál es un buen conjunto de grupos adimensionales independientes construidos a partir de G y estas cantidades?

Junto con el potencial (o voltaje) V, un actor principal en electromagnetismo es el campo eléctrico. (Una vez que entiendas cómo manejar los campos eléctricos, puedes practicar analizando campos magnéticos; prueba Problemas 5.31, 5.32 y 5.33). Los campos eléctricos no sólo transmiten fuerza, sino que también contienen energía. Esta energía es importante, sobre todo porque su transporte es como el Sol calienta la Tierra. Estimaremos la energía contenida en los campos eléctricos mediante análisis dimensional. Este análisis nos dará el resultado que utilizamos en la Sección 2.4.2 para estimar, por analogía, la energía en un campo gravitacional. Al igual que el campo gravitacional, el campo eléctrico se extiende sobre el espacio. Por lo tanto, normalmente no queremos la energía en sí, sino más bien la energía por volumen, la densidad de energía.

¿Cuál es la densidad de energía en un campo eléctrico?

Para responder a esta pregunta con análisis dimensional, sigamos la mayoría de los pasos que utilizamos para estimar la flexión de la luz estelar (Sección 5.3.1).

1. Enumerar las cantidades relevantes.

2. Formar grupos adimensionales independientes.

3. Usa los grupos para hacer la declaración más general sobre la densidad de energía.

4. Reduzca las posibilidades incorporando el conocimiento físico. Para este problema, podremos saltarnos este paso.

Así, el primer paso es tabular las cantidades de las que depende nuestro objetivo, la densidad\(\varepsilon\) energética. Definitivamente depende del campo eléctrico E. También depende probablemente de\(\epsilon_{0}\), la permitividad del espacio libre que aparece en la ley de Coulomb, porque la mayoría de los resultados en electrostática contienen\(\epsilon_{0}\). Pero no\(\varepsilon\) debería depender de la velocidad de la luz: La velocidad de la luz sugiere radiación, lo que requiere un campo eléctrico cambiante; sin embargo, incluso un campo eléctrico constante contiene energía. Así, nuestra lista podría estar completa. A ver, tratando de hacer un grupo adimensional.

Entonces enumeramos las cantidades con sus dimensiones, con el objetivo al frente de la mesa. La densidad de energía es energía por volumen, por lo que sus dimensiones son ML ⁻¹ T ⁻². El campo eléctrico es fuerza por carga (así como el campo gravitacional es fuerza por masa, ¡analogía!) , por lo que sus dimensiones son MLT ⁻² Q ⁻¹.

\(\varepsilon\)	ML ^-1 T ^-2	densidad de energía
E	MLT ^-2 Q ^-1	campo eléctrico
\(epsilon_{0}\)	M ^-1 L ^-3 T ^2 Q ^2	Constante SI

¿Cuáles son las dimensiones de\(\epsilon_{0}\)?

Esta cantidad es la más difícil. Aparece en la ley de Coulomb:

\[\textrm{electrostatic force} = \frac{q^{2}}{4 \pi \epsilon_{0}}\frac{1}{r^{2}}.\]

Como ecuación dimensional,

\[[\epsilon_{0}] = \frac{Q^{2}}{[F]L^{2}},\]

donde [F] = MLT ⁻² representa las dimensiones de la fuerza. Por lo tanto,\(\epsilon_{0}\) tiene dimensiones de M ⁻¹ L ⁻³ T ² Q ².

El segundo paso es encontrar grupos adimensionales independientes. Cualquier búsqueda es ayudada por saber cuántos elementos encontrar. Este recuento es proporcionado por el teorema de Buckingham Pi. Para aplicar el teorema, primero necesitamos contar las dimensiones independientes.

¿Cuántas dimensiones independientes contienen las tres cantidades?

A primera vista, las cantidades contienen cuatro dimensiones independientes: M, L, T y Q. Sin embargo, el teorema de Buckingham Pi entonces predeciría −1 grupos adimensionales, lo que no tiene sentido. En efecto, el número de dimensiones independientes no puede exceder el número de cantidades (restricción que explicaste en Problema 5.7). Aquí, como verifica en Problema\(\PageIndex{4}\), solo hay dos dimensiones independientes, por ejemplo, MLT ⁻² Q ⁻¹ (las dimensiones del campo eléctrico) y L ² Q ⁻¹.

Tres cantidades construidas a partir de dos dimensiones independientes producen un grupo adimensional independiente. Una opción útil para este grupo, porque es proporcional a la meta\(\varepsilon\), es\(\varepsilon/\epsilon_{0}E^{2}\).

El tercer paso es utilizar el grupo adimensional independiente para hacer la declaración más general sobre la densidad de energía. Con un solo grupo, la afirmación más general es

\[\varepsilon \sim \epsilon_{0}E^{2}.\]

El cuarto paso es estrechar las posibilidades mediante el uso del conocimiento físico. Con un solo grupo adimensional independiente, el espacio de posibilidades ya es estrecho. La única libertad es el prefactor adimensional oculto en el signo de aproximación simple ~; resulta ser 1/2. En la Sección 5.4.3, el escalado nos\(\varepsilon \: \alpha \: E^{2}\) ayudará a explicar el sorprendente comportamiento del campo eléctrico producido por una carga acelerada y, con ello, explicar por qué las estrellas son visibles y las radios funcionan.

Ejercicio\(\PageIndex{4}\): Rewriting the dimensions

Expresar las dimensiones de\(\varepsilon\), E, y\(\epsilon_{0}\) en términos de [E] (las dimensiones del campo eléctrico) y L ² Q ⁻¹. Así, mostrar que las tres cantidades contienen sólo dos dimensiones independientes.

Ejercicio\(\PageIndex{5}\): Dimensions of magnetic field

Un campo magnético B produce una fuerza sobre una carga móvil q dada por

\[\textbf{F} = q(\textbf{v} \times \textbf{B}),\]

donde v es la velocidad de la carga. Utilice esta relación para encontrar las dimensiones del campo magnético en términos de M, L, T y Q. Por lo tanto, dar la definición de un tesla, la unidad SI de campo magnético.

Ejercicio\(\PageIndex{6}\): Magnetic energy density

Así como dependen los campos eléctricos\(\epsilon_{0}\), la permitividad del espacio libre, los campos magnéticos dependen de la constante\(\mu_{0}\) llamada permeabilidad del espacio libre. Se define como

\[\mu_{0} \equiv 4 \pi \times 10^{-7} N A^{-2},\]

donde N es un newton y A es un amperio (un culombo por segundo). Expresar las dimensiones de\(\mu_{0}\) en términos de M, L, T y Q. Luego use las dimensiones del campo magnético (Problema\(\PageIndex{5}\)) para encontrar la densidad de energía en un campo magnético B. (Al igual que con el campo eléctrico, el prefactor adimensional será 1/2, pero el análisis dimensional no nos da esa información). ¿Qué analogías puedes hacer entre electrostática y magnetismo?

Ejercicio\(\PageIndex{7}\): Magnetic field due to a wire

Utilice las dimensiones de B (Problema\(\PageIndex{5}\)) y de la permeabilidad del espacio libre\(\mu_{0}\) (Problema\(\PageIndex{6}\)) para encontrar el campo magnético B a una distancia r de un cable infinitamente largo que transporta una corriente I. El prefactor adimensional faltante, que el análisis dimensional no puede decirnos, resulta ser\(1/2\pi\).

Las máquinas de resonancia magnética (MRI) para diagnóstico médico utilizan campos del orden de 1 tesla. Si este campo fuera producido por un cable portador de corriente a 0.5 metros de distancia, ¿qué corriente se requeriría? Por lo tanto, explique por qué estos campos magnéticos son producidos por imanes superconductores.

Ejercicio\(\PageIndex{8}\): Fields due to a uniform sheet of charge

Imagine una hoja de carga infinita y uniforme que contenga una carga por área\(\sigma\). Utilice el análisis dimensional para encontrar el campo eléctrico E a una distancia z de la hoja. (¡El prefactor adimensional faltante resulta ser 1!) Por lo tanto, dar el exponente de escala n in\(E \propto zn\). (En Problema 6.21, investigarás una explicación física de este sorprendente resultado.)

Utilice la analogía entre los campos eléctricos y gravitacionales (Sección 2.4.2) para encontrar el campo gravitacional por encima de una lámina uniforme con masa por área\(\sigma\).

5.4.3 Poder irradiado por una carga móvil

En nuestro siguiente ejemplo, estimaremos la potencia irradiada por una carga móvil, que es como funciona una antena de radiodifusión. Esta potencia, cuando se combina con nuestra larga comprensión del flujo (Sección 3.4.2) y nuestra nueva comprensión de la densidad de energía en un campo eléctrico (Sección 5.4.2), pronosticará una sorprendente relación de escala para la fuerza del campo de radiación, responsable de nuestra capacidad de ver el mundo. El ejemplo también ilustra una forma sencilla de gestionar las dimensiones de carga.

¿Cómo depende la potencia irradiada por una carga móvil de la aceleración de la carga?

Por el momento, ignoremos la velocidad de la carga. Lo más probable es que la dependencia de la aceleración sea una relación de escalado

\[\textrm{power} \propto (\textrm{acceleration})^{n}.\]

Encontraremos el exponente de escalado n mediante análisis dimensional.

Primero, enumeramos las cantidades de las que depende la meta, la potencia radiada P. Ciertamente depende del movimiento de la carga, que está representado por su aceleración a. También depende de la cantidad de carga q, porque más carga probablemente signifique más radiación. La lista también debe incluir la velocidad de la luz c, porque la radiación viaja a la velocidad de la luz.

Probablemente también necesite la permitividad del espacio libre\(\epsilon_{0}\). Sin embargo, en lugar de incluir\(\epsilon_{0}\) directamente, reutilicemos el atajo para la gravitación, donde combinamos la constante G de Newton con una masa (en la Sección 5.3.1). De igual manera,\(\epsilon_{0}\) siempre aparece como\(q^{2}/4 \pi \epsilon_{0}\), ya sea en energía electrostática o fuerza. Por lo tanto, en lugar de incluir q y\(\epsilon_{0}\) por separado, podemos incluir únicamente\(q^{2}/4 \pi \epsilon_{0}\).

¿Qué pasó con la velocidad de la carga?

Si la potencia irradiada dependiera de la velocidad, entonces podríamos usar el principio de relatividad para hacer una máquina de movimiento perpetuo: Generamos energía simplemente usando un marco de referencia diferente (inercial), uno en el que la carga se mueve más rápido. Más que creer en el movimiento perpetuo, debemos concluir que la velocidad no afecta al poder. Equivalentemente, podemos eliminar la velocidad cambiando a un marco de referencia donde la carga tiene velocidad cero.

¿Por qué el argumento del marco de referencia no nos permite eliminar la aceleración?

Depende de cambiar a otro marco de referencia inercial, es decir, un marco que se mueve a una velocidad constante en relación con el marco original. Este movimiento relativo no afecta a la aceleración de la carga, solo a su velocidad.

Sin embargo, si cambiamos a un marco de referencia no inercial, acelerante, debemos modificar las ecuaciones de movimiento, agregando términos para las fuerzas Coriolis, centrífuga y Euler. (Para más información sobre los marcos de referencia, una exposición maravillosa es la Mecánica Clásica de John Taylor [45].) Si cambiamos a un marco no inercial, todas las apuestas están apagadas sobre la potencia radiada. En resumen, la aceleración es diferente de la velocidad

P	ML ^2 T ^-3	potencia radiada
\(q^{2}/4 \pi \epsilon_{0}\)	ML ^3 T ^-2	desorden electrostático
c	LT ^-1	velocidad de la luz
a	LT ^-2	aceleración

Estas cuatro cantidades, construidas a partir de tres dimensiones independientes, producen solo un grupo adimensional independiente. Debido a que la masa aparece solo en P y\(q^{2}/4 \pi \epsilon_{0}\) (como M ¹), el grupo debe contener\(P/(q^{2}/4 \pi \epsilon_{0})\). Este cociente tiene dimensiones de L ⁻¹ T ⁻¹. Multiplicarlo por\(c^{3}/a^{2}\), que tiene dimensiones de LT, hace que el resultado sea adimensional. Por lo tanto, el grupo adimensional independiente proporcional a P es

\[\frac{P}{q^{2}/4 \pi \epsilon_{0}} \frac{c^{3}}{a^{2}}.\]

Como único grupo, debe ser una constante adimensional, por lo que

\[P \sim \frac{q^{2}}{4 \pi \epsilon_{0}} \frac{a^{2}}{c^{3}}.\]

El resultado exacto es casi idéntico

\[P = \frac{q^{2}}{6 \pi \epsilon_{0}} \frac{a^{2}}{c^{3}}.\]

Este resultado es incluso correcto a velocidades relativistas, siempre y cuando usemos la aceleración relativista (la cuatro aceleración) como generalización de a.

Como relación de escalado entre P y a, es simple:\(P \alpha a^{2}\). Duplicar la aceleración cuadruplica la potencia radiada. La fuerte dependencia de la aceleración es una parte importante de la razón por la que el cielo es azul (haremos el análisis en la Sección 9.4.1).

Esta energía es transportada por un campo eléctrico cambiante. Mediante el uso de la densidad de energía en el campo eléctrico, podemos estimar y explicar la sorprendente fuerza de este campo. Comenzamos por estimar el flujo de energía (la potencia por área) a una distancia r, extendiendo la potencia radiada sobre una esfera de radio r. La superficie de la esfera es comparable a r ², por lo que

\[\textrm{energy flux} \sim \frac{P}{r^{2} \sim \frac{q^{2}}{4 \pi \epsilon_{0}} \frac{a^{2}}{c^{3}} \frac{1}{r^{2}}.\]

El flujo de energía, basado en lo que aprendimos en la Sección 3.4.2, está conectado a la densidad de energía mediante

\[\textrm{energy flux} = \textrm{energy density} \times \textrm{transport speed}.\]

La velocidad de transporte es la velocidad de la luz c, por lo que

\[\underbrace{\frac{q^{2}}{4 \pi \epsilon_{0}} \frac{a^{2}}{c^{3}} \frac{1}{r^{2}}}_{\textrm{energy flux}} \sim \underbrace{\epsilon_{0}E^{2}}_{\textrm{energy density}} \times \underbrace{c.}_{\textrm{speed}}\]

Ahora podemos resolver para el campo eléctrico:

\[E \sim \frac{qa}{\epsilon_{0}c^{2}} \frac{1}{r}.\]

Como relación de escalado,\(E \alpha r^{-1}\). Compárelo con el exponente de escala −2 para un campo electrostático, donde\(E \alpha r^{-2}\) (ley de Coulomb). Por lo tanto, el campo de radiación cae más lentamente con la distancia que el campo electrostático. Esta importante diferencia explica por qué podemos recibir señales de radio y ver estrellas. Si los campos de radiación fueran proporcionales a 1\(1/r^{2}\), las estrellas, y la mayor parte del mundo, serían invisibles. ¡Qué diferencia puede hacer un exponente de escala!