1.2: Modelos ODE de primer orden

Modelos ODE de primer orden

Los sistemas eléctricos, mecánicos, térmicos y fluidos que contienen un solo elemento de almacenamiento de energía se describen mediante modelos ODE de primer orden.

\(u(t)\)Denote una entrada genérica,\(y(t)\) denote una salida genérica y\(\tau\) denote la constante de tiempo; entonces, un modelo genérico de ODE de primer orden se expresa como:\[\tau \frac{dy(t)}{dt} +y(t)=u(t)\]

La constante de tiempo,\(\tau\), denota el tiempo en que la respuesta del sistema a una entrada constante se eleva a 63.2% de su valor final. La constante de tiempo se mide en\(\left[sec\right]\).

Ejemplos

Ejemplo\(\PageIndex{1}\)

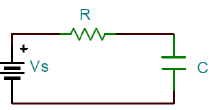
Una red RC en serie está conectada a través de una fuente de voltaje constante,\(V_\rm s\) (Figura 1.2.1). La ley de voltaje (KVL) de Kirchhoff se utiliza para modelar el comportamiento del circuito como:\(v_{R} +v_{C} =V_s\)

En las letras mayúsculas anteriores representan valores constantes y las letras minúsculas representan cantidades variables en el tiempo.

Vamos a\(v_{C} =v_{0}\) definir la salida del circuito; entonces,\(v_{R} =iR=RC\frac{dv_{0} }{dt}\), por lo tanto

\[RC\frac{dv_{0} (t)}{dt} +v_{0} (t)=V_s\]

La constante de tiempo del circuito RC se da como:\(\tau = RC\).

Figura\(\PageIndex{1}\): Un circuito RC en serie accionado por una fuente de voltaje constante.

Ejemplo\(\PageIndex{2}\)

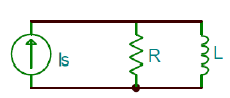
Una red RL paralela está conectada a través de una fuente de corriente constante,\(I_\rm s\) (Figura 1.2.2). El circuito es modelado por una ODE de primer orden, donde la variable de interés es la corriente inductora,\(i_{L}\), y la ley actual de Kirchhoff (KCL) se aplica en un nodo para obtener:\(i_{R} +i_{L} =I_\rm s\).

Al sustituir\(i_{R} =\frac{v}{R} =\frac{L}{R} \frac{di_{L} }{\rm dt}\) obtenemos la descripción ODE del circuito RL como:

\[\frac{L}{R} \frac{di_{L} (t)}{dt} +i_{L} (t)=I_s\]

La constante de tiempo del circuito RL se da como:\(\tau = \frac{L}{R}\).

Figura\(\PageIndex{2}\): Circuito RL paralelo accionado por una fuente de corriente constante.

Ejemplo\(\PageIndex{3}\)

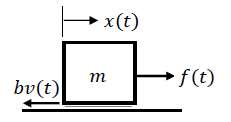
El movimiento de una masa inercial,\(m\), actuada por una fuerza,\(f(t)\), en presencia de fricción cinética, representada por\(b\), se rige por la segunda ley del movimiento de Newton (Figura 1.2.3). Dejar\(v\left(t\right)\) representar la velocidad; entonces, la fuerza resultante sobre el elemento de masa es:\(f-bv\). De ahí

\[m\frac{dv(t)}{dt} +bv(t)=f(t)\]

La constante de tiempo para el modelo mecánico es:\(\tau =\frac{m}{b}\), que describe la velocidad a la que se acumula la velocidad en respuesta a una entrada de fuerza constante.

Figura\(\PageIndex{3}\): Movimiento de una masa inercial con fuerza aplicada bajo fricción superficial.

Ejemplo\(\PageIndex{4}\)

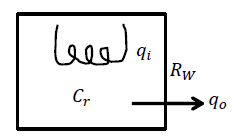
Se desarrolla un modelo para calefacción de habitaciones de la siguiente manera (Figura 1.2.4): dejar\(q_{i}\), denotar entrada de calor,\(C_{r}\) denotar la capacidad térmica de la habitación,\(\theta _{r}\) denotar la temperatura ambiente,\(\theta _{a}\) denotar la temperatura ambiente y\(R_{w}\) denotar una resistencia térmica que representa el aislamiento de la pared; entonces, la ecuación del balance de energía térmica se da como:

\[C_{r} \frac{d\theta_{r} }{dt} +\frac{\theta_{r} -\theta_{a} }{R_{w} } =q_{i}\]

En cuanto al diferencial de temperatura\(\Delta \theta =\theta _{r} -\theta _{a}\), la ODE gobernante es:

\[R_{w} C_{r} \frac{ d\Delta \theta }{ dt} +\Delta \theta =R_{w} q_{i}\]

Al comparar con el modelo genérico de ODE de primer orden\(\tau \frac{\rm dy}{\rm dt} +y=u\),, la constante de tiempo térmica se describe como:\(\tau =R_{w} C_{r}\). Además, la temperatura se mide en\([{}^\circ C]\), el flujo de calor se mide en\([W]\), la capacitancia térmica se mide en\(\left[\frac{J}{{}^\circ C}\right]\), y la resistencia térmica se mide en\(\left[\frac{{}^\circ C}{W}\right]\).

Figura\(\PageIndex{4}\): Un modelo de calefacción de habitaciones con fuente de calor y salida a través de las paredes.

Ejemplo\(\PageIndex{5}\)

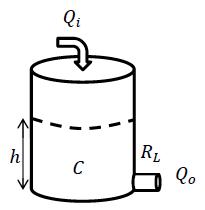
Un depósito cilíndrico se llena con un fluido incompresible suministrado desde una entrada con una salida controlada a través de una válvula hidráulica en la parte inferior (Figura 1.2.5).

Dejar\(P\) denotar la presión hidráulica,\(A\) denotar el área del reservorio,\(h\) denotar la altura,\(V\) denotar el volumen,\(\rho\) denotar la densidad de masa,\(R_{l}\) denotar la resistencia de la válvula al flujo de fluido,\(q_{ in} ,\; q_{out}\) denotar los caudales volumétricos, y\(g\) denotan la constante gravitacional; entonces, la presión base en el reservorio se obtiene como:\[P=P_{atm} +\rho gh=P_{atm} +\frac{\rho g}{A} V\]

La capacitancia del yacimiento se define como:\(C_{h} =\frac{dV}{dP} =\frac{A}{\rho g}\); entonces, la ecuación gobernante para el flujo hidráulico a través del yacimiento se da como:\[C_{h} \frac{dP}{dt} =q_{ in} -\frac{P-P_{atm} }{R_{l} }\]

En cuanto a la diferencia de presión, la ecuación se escribe como:\[R_{l} C_{h} \frac{d\Delta P}{ dt} +\Delta P=R_{l} q_{in} .\] Al comparar con el modelo genérico de ODE de primer orden\(\tau \frac{dy}{dt} +y=u\),, la constante de tiempo hidráulica se describe como:\(\tau =R_{w} C_{r}\).

Además, sustituyendo:\(\mathit{\Delta}P=\rho gh\) y\(C_h=\frac{A}{\rho g}\), podemos expresar de manera equivalente la ODE en términos de la altura del líquido,\(h\left(t\right)\), en el reservorio como:

\[AR_l\frac{dh}{dt}+\rho gh=R_lq_{in}\]

En lo anterior, la presión hidráulica se mide en\(\left[\frac{N}{m^2}\right]\), el flujo volumétrico se mide en\(\left[\frac{m^3}{s}\right]\), la capacitancia hidráulica se mide en\(\left[\frac{m^5}{N}\right]\), y la resistencia al flujo se mide en\(\left[\frac{Ns}{m^5}\right]\).

Figura\(\PageIndex{5}\): Un depósito hidráulico con flujo de entrada y salida a través de la válvula de fondo.

Resolución del modelo ODE de primer orden

Considerar la respuesta de un modelo ODE de primer orden:\(\tau \frac{dy\left(t\right)}{dt}+y\left(t\right)=u(t)\) a una función de forzamiento escalonado.

Al aplicar la transformada de Laplace con condiciones iniciales:\(y\left(0\right)=y_0\), obtenemos una ecuación algebraica:

\[\tau \left(sy\left(s\right)-y_0\right)+y(s)=u(s)\]

Asumimos una entrada de paso de unidad\(u\left(t\right)\), donde\(u\left(s\right)=\frac{1}{s}\); entonces, la salida se resuelve como:

\[y\left(s\right)=\frac{1}{s\left(\tau s+1\right)}+\frac{\tau y_0}{\tau s+1}\]

Usamos expansión de fracción parcial (PFE) para expresar la salida como:

\[y\left(s\right)=\frac{1}{s}-\frac{\tau }{\tau s+1}+\frac{\tau y_0}{\tau s+1}\]

Mediante el uso de la transformada inversa de Laplace, obtenemos la solución de dominio de tiempo para la ODE como:

\[y\left(t\right)=1+\left(y_0-1\right)e^{-t/\tau },\ \ t\ge 0\]

Deje que el valor de estado estacionario de la salida se denote como:\(y_{\infty }={\mathop{lim}_{t\to \infty } y(t)\ }\); entonces, la respuesta escalonada de un modelo general de ODE de primer orden se expresa como:

\[y\left(t\right)=\left[y_{\infty }+\left(y_0-y_{\infty }\right)e^{-t/\tau }\right]u\left(t\right)\]

En lo anterior,\(u\left(t\right)\) denota una función de paso unitario, utilizada para mostrar causalidad, es decir, la respuesta es válida para\(t\ge 0\).

Función de transferencia

La descripción de la función de transferencia de un sistema dinámico se obtiene a partir del modelo ODE mediante la aplicación de la transformada de Laplace asumiendo cero condiciones iniciales. La función de transferencia describe la relación entrada-salida en forma de función racional, es decir, una relación de dos polinomios en la variable Laplace\(s\).

Un modelo ODE de primer orden con entrada\(u(t)\) y salida\(y(t)\) se describe como:\(\tau \frac{\rm dy(t)}{\rm dt} +y(t)=u(t)\).

Para el modelo de primer orden, la aplicación de la transformada Laplace con cero condiciones iniciales da:\((\tau s+1)y(s)=u(s)\).

La función de transferencia de entrada-salida resultante se da como:

\[\frac{y(s)}{u(s)} =\frac{1}{\tau s+1}\]

Respuesta de salida

Para condiciones iniciales cero,\(y_0=0\), la salida se expresa como:

\[y\left(t\right)=\left(1-e^{-t/\tau }\right)u\left(t\right)\]

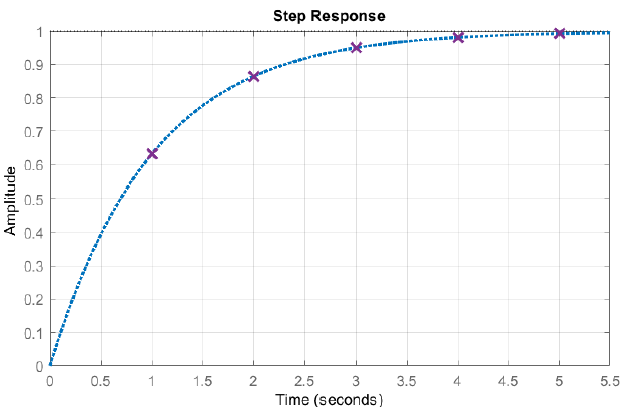
La respuesta del sistema para\(\tau =1\,sec\) se grafica en la Figura 1.5.

Los valores de salida en los momentos seleccionados,\(t=k\tau ,\ \ k=0,1,\dots\) se compilan en la siguiente tabla. Por convención, se supone que la salida ha alcanzado el estado estacionario cuando alcanza el 98% de su valor final. De ahí que el tiempo de asentamiento del sistema se exprese como:\(t_s=4\tau\).

Cuadro 1.1: La respuesta escalonada de un modelo de primer orden en instancias de tiempo seleccionadas.

Tiempo	Valor de salida
0	\(y\left(0\right)=0\)
1\(\tau\)	\(1-e^{-1}\cong 0.632\)
2\(\tau\)	\(1-e^{-2}\cong 0.865\)
3\(\tau\)	\(1-e^{-3}\cong 0.950\)
4\(\tau\)	\(1-e^{-4}\cong 0.982\)
5\(\tau\)	\(1-e^{-5}\cong 0.993\)

Figura\(\PageIndex{6}\): Respuesta de un modelo de ODE de primer orden (\(\tau=1 sec\)).

pkg load control
s=tf('s');
Gs=1/(s+1);
step(Gs), hold
plot(1:5,1-exp(-(1:5)),'x')