1.3: El Teorema de Proyección

Considere el siguiente problema de minimización:

\[\min _{m \in M}\|y-m\|\]

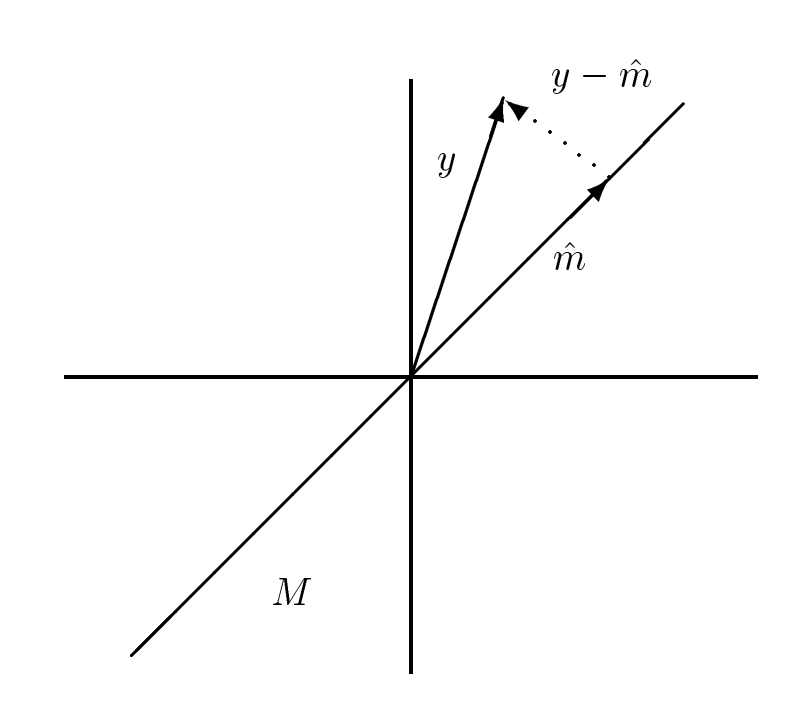
donde la norma se define a través de un producto interno. El teorema de proyección (sugerido por la figura siguiente), establece que la solución óptima\(\hat{m}\) se caracteriza de la siguiente manera:

\[(y-\hat{m}) \perp M\]

Para verificar este teorema, asuma lo contrario. Entonces existe un\(m_{0},\left\|m_{0}\right\|\) = 1, tal que\(<y-\hat{m}, m_{0}>=\delta \neq 0\). Ahora argumentamos que\(\left(\hat{m}+\delta m_{0}\right) \in M\) logra un valor menor al problema de minimización anterior. En particular,

\ [\ begin {alineado}
\ izquierda\ |y-\ hat {m} -\ delta m_ {0}\ derecha\ |^ {2} &=\ |y-\ hat {m}\ |^ {2} --+|<y-\ hat {m},\ delta m_ {0} > \<\ delta m_ {0}, y-\ hat {m} > delta|^ {2}\ izquierda\ |m_ {0}\ derecha\ |^ {2}\ &=\
|y-\ sombrero {m}\ ^ {2} -|\ delta|^ {2} -|\ delta|^ {2} +|\ delta|^ {2}\\ &=\
|y-\ sombrero {m}\ |^ { 2} -|\ delta|^ {2}
\ final {alineado}\]

Esto contradice la optimalidad de\ (\ hat {m}).

• Dado un subespacio\(\mathcal{S}\), mostrar que cualquier vector x puede escribirse de manera única como\(x=x_{\mathcal{S}}+x_{\mathcal{S}^{\perp}}\), dónde\(x_{\mathcal{S}} \in \mathcal{S}\) y\(x_{\mathcal{S} \perp} \in \mathcal{S}^{\perp}\).