7.2: Descripción general

Para un sistema causal con\(m\) entradas\(u_{j}(t)\) y\(p\) salidas\(y_{i}(t)\) (por lo tanto, variables\(m+ p\) manifiestas), una descripción del espacio de estado de\(n\) orden th es aquella que introduce variables\(n\) latentes\(x_{l}(t)\) llamadas variables de estado con el fin de obtener un particular formulario para las restricciones que definen el modelo. Dejar

\ [u (t) =\ left [\ begin {array} {c}
u_ {1} (t)\\
\ vdots\\
u_ {m} (t)
\ end {array}\ right],\ quad y (t) =\ left [\ begin {array} {c}
y_ {1} (t)\
\ vdots\\
y_ {p} (t)
\ end {array}\ derecha],\ quad x (t) =\ izquierda [\ begin { array} {c}
x_ {1} (t)\\
\ vdots\\
x_ {n} (t)
\ end {array}\ derecha]\ nonumber\]

una descripción\(n\) del espacio de estado de orden th-order toma la forma

\[\underbrace{\dot{x}(t)=f(x(t), u(t), t)}_{\text{state evolution equations}} \label{7.1}\]

\[\underbrace{y(t)=g(x(t), u(t), t)}_{\text{instantaneous output equations}} \label{7.2}\]

Para guardar la escritura de las mismas ecuaciones para el tiempo continuo y discreto, interpretamos

\[\dot{x}(t)=\frac{d x(t)}{d t}, t \in \mathbb{R} \text { or } \mathbb{R}^{+} \nonumber\]

para sistemas de TC, y

\[\dot{x}(t)=x(t+1), \quad t \in \mathbb{Z} \text { or } \mathbb{Z}^{+}\nonumber\]

para sistemas DT. Solo consideraremos modelos estado-espacio de orden finito (o finito-dimensional, o agrupados), aunque también hay una teoría bastante bien desarrollada (pero mucho más sutil y técnica) de modelos estado-espacio de orden infinito (o infinito-dimensionales, o distribuidos).

Modelos DT

La característica clave de una descripción estado-espacio es la siguiente propiedad, a la que nos referiremos como la propiedad estatal. Dado el vector de estado presente (o “estado”) y la entrada presente en el momento\(t\), podemos calcular: (i) la salida actual, usando la Ecuación\ ref {7.2}; y (ii) el siguiente estado usando la Ecuación\ ref {7.1}. Es fácil ver que esto nos pone en condiciones de hacer lo mismo a la vez\(t + 1\), y por lo tanto de continuar el proceso en cualquier intervalo de tiempo. Ampliando este argumento, podemos hacer la siguiente afirmación:

Así, el estado en cualquier momento\(t_{0}\) resume todo lo relacionado con el pasado que sea relevante para el futuro. Teniendo en cuenta este hecho -que las variables de estado son las variables de memoria (o, en situaciones más físicas, las variables de almacenamiento de energía) de un sistema- a menudo nos guía rápidamente hacia buenas elecciones de variables de estado en cualquier contexto dado.

Modelos CT

La misma propiedad estatal resulta sostenerse en el caso de CT, al menos para\(f ( . )\) eso se comportan lo suficientemente bien como para que las ecuaciones de evolución de estado tengan una solución única para todas las entradas de interés y sobre todo el eje de tiempo | estos serán típicamente los únicos tipos de sistemas de TC de interés para nosotros. Una demostración de esta afirmación, y una elucidación de las condiciones precisas bajo las cuales se sostiene, requeriría una excursión a la teoría de las ecuaciones diferenciales más allá de lo apropiado para este curso. Podemos hacer que este resultado sea plausible, sin embargo, considerando la aproximación de la serie Taylor

\[\begin{align} x\left(t_{0}+\epsilon\right) &\approx x\left(t_{0}\right)+\left(\frac{d x(t)}{d t}\right)_{t=t_{0}} \epsilon\ \label{7.3} \\[4pt] &=x\left(t_{0}\right)+f\left(x\left(t_{0}\right), u\left(t_{0}\right), t_{0}\right) \epsilon \label{7.4} \end{align}\]

donde la segunda ecuación resulta de aplicar la ecuación de evolución del estado\ ref {7.1}. Esto sugiere que podemos calcular aproximadamente\(x(t_{0} + \epsilon)\), dado\(x(t_{0})\) y\(u(t_{0})\); el error en la aproximación es de orden\(\epsilon^{2}\), y por lo tanto se puede hacer más pequeño haciendo\(\epsilon\) más pequeño. Para que se porten suficientemente bien\(f ( . )\), de manera similar podemos dar un paso adelante desde\(t_{0}+\epsilon \text { to } t_{0}+2 \epsilon\), y así sucesivamente, llegando eventualmente a la última hora\(t_{f}\), tomando el orden de\(\epsilon^{-1}\) los pasos en el proceso. El error acumulado en el momento\(t_{f}\) es entonces de orden\(\epsilon^{-1} \cdot \epsilon^{2}=\epsilon\), y puede hacerse arbitrariamente pequeño haciendo\(\epsilon\) lo suficientemente pequeño. También tenga en cuenta que, una vez que se determina el estado en cualquier momento y se conoce la entrada en ese momento, entonces la salida en ese momento viene dada inmediatamente por la Ecuación\ ref {7.2}, incluso en el caso CT.

La aproximación simple de la serie Taylor en la Ecuación\ ref {7.4} corresponde al más crudo de los esquemas numéricos -el método “Euler hacia adelante ”- para integrar un sistema de ecuaciones de la forma en la Ecuación\ ref {7.1}. Existen esquemas mucho más sofisticados (por ejemplo, métodos Runge-Kutta, esquemas Adams-Gear para sistemas “rígidos” que exhiben escalas de tiempo muy diferentes, etc.), pero el esquema Euler hacia adelante es suficiente para hacer plausible el hecho de que la propiedad estatal resaltada anteriormente se aplique tanto a los sistemas CT como a los DT.

Ejemplo 7.1 Circuito RC

Este ejemplo demuestra un punto fino en la definición de un estado para los sistemas de TC. Considere un circuito RC en serie con una fuente de voltaje\(u\). Usando KVL, obtenemos la siguiente ecuación que describe el sistema:

\[-u+v_{R}+R C \dot{v}_{C}=0\nonumber\]

Es claro que\(v_{C}\) define un estado para el sistema como lo describimos anteriormente. ¿\(v_{R}\)Define un estado? Si\(v_{R}(t_{0})\) se da, y\(u(t), t_{0} \leq t < t_{f}\) se conoce la entrada, entonces se puede calcular\(v_{C}(t_{0})\) y usar la propiedad state se\(v_{C}(t_{f})\) puede calcular a partir de la cual se\(v_{R}(t_{f})\) puede calcular. Esto dice que\(v_{R}(t)\) define un estado que contradice nuestra intuición ya que no es un componente de almacenamiento de energía.

Hay una solución fácil de este problema si asumimos que todas las entradas son funciones continuas por partes. En ese caso definimos la propiedad state como la capacidad de calcular valores futuros del estado a partir del valor inicial\(x(t_{0})\) y la entrada\(u(t), t_{0} < t < t_{f}\). Observe la estricta desigualdad. Te dejamos verificar que esta definición descarta\(v_{R}\) como variable de estado.

Linealidad e invarianza en el tiempo

Si en la descripción estado-espacio en la Ecuación\ ref {7.1}, (7.2), tenemos

\[f(x(t), u(t), t)=f(x(t), u(t))\ \tag{7.5}\]

\[g(x(t), u(t), t)=g(x(t), u(t))\ \tag{7.6}\]

entonces el modelo es invariante en el tiempo (en el sentido definido anteriormente, para modelos de comportamiento). Esto corresponde a requerir invarianza temporal de las funciones que especifican cómo se combinan las variables de estado y las entradas para determinar la evolución del estado y las salidas. Los resultados de los experimentos en un sistema invariable en el tiempo dependen únicamente de las entradas y del estado inicial, no de cuándo se realizan los experimentos.

Si, por otro lado, las funciones\(f ( . )\) y\(g( . )\) en la descripción estado-espacio son funciones lineales de las variables de estado y entradas, es decir, si

\[f(x(t), u(t), t)=A(t) x(t)+B(t) u(t) \label{7.7}\]

\[g(x(t), u(t), t)=C(t) x(t)+D(t) u(t) \label{7.8}\]

entonces el modelo es lineal, nuevamente en el sentido conductual. El caso de un modelo lineal y de variación periódica (LPV) suele ser de interés; cuando\(A(t) = A(t + T ), B(t) = B(t + T ), C(t) = C(t + T )\), y\(D(t) = D(t + T )\) para todos\(t\), el modelo es LPV con periodo\(T\).

De aún más importancia para nosotros es el caso de un modelo que es lineal e invariable en el tiempo (LTI). Para un modelo LTI, la descripción del espacio de estado simplifica a

\[f(x(t), u(t), t)=A x(t)+B u(t) \label{7.9} \]

\[g(x(t), u(t), t)=C x(t)+D u(t) \label{7.10}\]

Estudiaremos principalmente modelos LTI en este curso. Tenga en cuenta que los modelos LTI estado-espacio a veces se\((A, B, C, D)\) designan como

\ [\ left [\ begin {array} {c|c}
A & B\
\ hline C & D
\ end {array}\ derecha]\ nonumber\]

ya que estas cuatro matrices especifican completamente el modelo estado-espacio.

Cuadro 7.1: Algunos ejemplos de descripciones de estado-espacio lineales, no lineales, variables en el tiempo, variables periódicamente e invariantes en el tiempo.

Sistema	Tipo
\(\dot{x}(t)=tx^{2}(t)\)	NLTV
\(\dot{x}(t)=x^{2}(t)\)	NLTI
\(\dot{x}(t)=t x(t)\)	LTV
\(\dot{x}(t)=(\cos t) x(t)\)	LPV
\(\dot{x}(t)= x(t)\)	LTI

Algunos ejemplos de las diversas clases de sistemas enumerados anteriormente se dan en la Tabla 7.1. A continuación se presentan ejemplos más elaborados.

Se podría pensar que la formulación estado-espacio es restrictiva ya que solo involucra derivados de primer orden. Sin embargo, al elegir adecuadamente las variables de estado, se pueden describir dinámicas de orden superior. Los ejemplos en esta sección y sobre la tarea lo dejarán claro.

Ejemplo 7.2: Sistema Masa-Muelle

Para el sistema masa-resorte en el Ejemplo 6.2, derivamos la siguiente representación del sistema:

\[M \ddot{z}=-k z+u\nonumber\]

Para poner esto en forma de espacio de estado, elija posición y velocidad como variables de estado:

\ [\ begin {array} {l}
x_ {1} =z\\
x_ {2} =\ punto {z}\ (7.11)
\ end {array}\ nonumber\]

Por lo tanto,

\ [\ begin {alineado}
\ punto {x} _ {1} &=\ punto {z} =x_ {2}\
\ punto {x} _ {2} &=-\ frac {k} {M} {M} z+\ frac {1} {M} u=-\ frac {k} {M} {M} x_ {1} +\ frac {1} {M} u
\ fin alineado}\ nonumber\]

La entrada es la fuerza\(u\) y deja que la salida sea la posición de la masa. La descripción del espacio de estado resultante de este sistema es

\ [\ left [\ begin {array} {c}
\ dot {x} _ {1}\
\ dot {x} _ {2}
\ end {array}\ right] =\ left [\ begin {array} {c}
x_ {2}\
-\ frac {k} {M} {M} x_ {1} +\ frac {1} {M} u
\ end {array}\ derecha]\ nonumber\]

\ [\ begin {ecuación}
y=x_ {1}
\ end {ecuación}\ nonumber\]

El ejemplo anterior sugiere algo que es cierto en general para los sistemas mecánicos: las variables de estado natural son las variables de posición y velocidad (asociadas con la energía potencial y la energía cinética respectivas

Ejemplo 7.3: Circuito no lineal

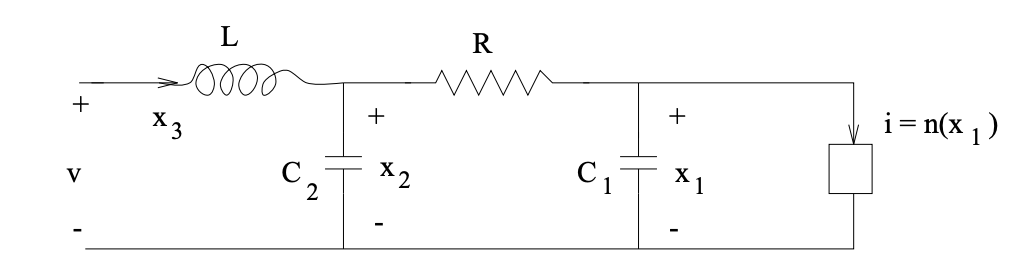
Figura\(\PageIndex{1}\): Circuito no lineal

Deseamos poner las relaciones que describen el comportamiento del circuito anterior en forma de estado- espacio, tomando el voltaje\(v\) como entrada y eligiendo como variables de salida el voltaje a través del elemento no lineal y la corriente a través del inductor. La relación constituyente para la admitancia no lineal en el diagrama de circuito es\(i_{nonlin} = \mathcal{N} (v_{nonlin})\), donde\(N ( . )\) denota alguna función no lineal.

Intentemos tomar como variables de estado las tensiones del condensador y la corriente del inductor, porque estas variables representan los mecanismos de almacenamiento de energía en el circuito. La descripción correspondiente del espacio de estado expresará las tasas de cambio de estas variables en términos de los valores instantáneos de estas variables y el valor instantáneo de la tensión de entrada\(v\). Es natural, por lo tanto, buscar expresiones para\(C_{1} \dot{x}_{1}\) (la corriente a través\(C_{1}\), para\(C_{2} \dot{x}_{2}\) (la corriente a través\(C_{2}\), y para\(L \dot{x}_{3}\) (la tensión a través\(L\)).

Aplicando KCL al nodo donde\(R\)\(C_{1}\), y el dispositivo no lineal se encuentran, obtenemos

\[C_{1} \dot{x}_{1}=\frac{\left(x_{2}-x_{1}\right)}{R}-\mathcal{N}\left(x_{1}\right)\nonumber\]

Aplicando KCL al nodo donde\(R\),\(C_{2}\) y nos\(L\) encontramos,

\[C_{2} \dot{x}_{2}=x_{3}-\frac{\left(x_{2}-x_{1}\right)}{R}\nonumber\]

Finalmente, KVL aplicado a un bucle que contiene\(L\) rendimientos

\[L \dot{x}_{3}=v-x_{2}\nonumber\]

Ahora podemos combinar estas tres ecuaciones para obtener una descripción estado-espacio de este sistema:

\ [\ left [\ begin {array} {c}
\ punto {x} _ {1}\
\ punto {x} _ {2}\
\ punto {x} _ {3}
\ end {array}\ derecha] =\ izquierda [\ begin {array} {c}
\ frac {1} {C_ {1}}\ left (\ frac {x_ {2} -x_ {1}}} {R} -\ mathcal {N}\ izquierda (x_ {1}\ derecha)\ derecha)\
\ frac {1} {C_ {2}}\ izquierda (x_ {3} -\ frac {x_ {2} -x_ {1}} {R}\ derecha)\\
-\ frac {1} {L} x_ {2}
\ end {array}\ derecha] +\ izquierda [\ begin {array} {c}
0\\
0\
\ frac {1} {L} v
\ end {array}\ derecha]\\ tag {7.12}\]

\ [y=\ left [\ begin {array} {l}
x_ {1}\\
x_ {3}
\ end {array}\ derecha]\ etiqueta {7.13}\]

Observe que las variables de salida son descritas por una ecuación de salida instantánea de la forma (7.2). Esta descripción estado-espacio es invariable en el tiempo pero no lineal. Esto tiene sentido, ¡porque el circuito sí contiene un elemento no lineal!

Ejemplo 7.4: Discretización

Supongamos que tenemos un sistema de tiempo continuo descrito en forma estado-espacio por

\ [\ comenzar {alineado}
\ frac {d x (t)} {d t} &=A x (t) +B u (t)\\
y (t) &=C x (t) +D u (t)
\ final {alineado}\ nonumber\]

Muestreemos ahora este sistema con un periodo de\(T\), y aproximemos la derivada como una diferencia hacia adelante:

\[\frac{1}{T}(x((k+1) T)-x(k T))=A x(k T)+B u(k T), \quad k \in \mathbb{Z} \label{7.14}\]

Es conveniente cambiar nuestra notación, escritura\(x[k] \equiv x(k T)\), y de manera similar para\(u\) y\(y\). Por lo tanto, nuestra ecuación muestreada puede ser reescrita como

\ [\ begin {alineado}
x [k+1] & =( I+T A) x [k] +T B u [k]\\
&=\ hat {A}\ mathbf {x} [k] +\ hat {B}\ mathbf {u} [k]\
y [k] &=C x [k] +D u [k]\ (7.15)
\ end {alineado}\ nonumber\]

que está en forma estandar estado-espacio.

En muchas aplicaciones modernas, los sistemas de control se implementan digitalmente. Para ello, el ingeniero de control debe ser capaz de analizar tanto los sistemas discretos de tiempo como los sistemas de tiempo continuo. En este ejemplo se utilizó un método de muestreo crudo para obtener un modelo de tiempo discreto a partir de uno de tiempo continuo. Discutiremos métodos de discretización más refinados más adelante en este libro.

También es importante señalar que existen fenómenos físicos que requieren o sugieren directamente modelos de tiempo discreto; no todos los modelos de tiempo discreto que uno encuentra en las aplicaciones son discretizaciones de los de tiempo continuo.