13.1: Nociones de Estabilidad

Para un sistema general no accionado

\[\begin{align} \dot{x}(t) &=f(x(t), 0, t) \quad(C T) \label{13.1}\\[4pt] x(k+1) &=f(x(k), 0, k) \quad(D T) \label{13.2} \end{align}\]

decimos que un punto\(\bar{x}\) es un punto de equilibrio a partir del tiempo\(t_{0}\) para el sistema CT anterior si\(f(\bar{x}, 0, t)= 0, \forall t \geq t_{0}\), y es un punto de equilibrio a partir del tiempo\(k_{0}\) para el sistema DT por encima de si\(f(\bar{x}, 0, k)= \bar{x}, \forall k \geq k_{0}\). Si el sistema se inicia en el estado\(\bar{x}\) en el momento\(t_{0}\) o\(k_{0}\), permanecerá ahí para siempre. Los sistemas no lineales pueden tener múltiples puntos de equilibrio (o equilibrios). (Otra clase de soluciones especiales para sistemas no lineales son las soluciones periódicas, pero aquí solo nos centraremos en los equilibrios). Nos gustaría caracterizar de alguna manera la estabilidad de los equilibrios. Por ejemplo, ¿tiende el estado a regresar al punto de equilibrio después de una pequeña perturbación alejada de él? ¿Permanece cerca del punto de equilibrio en algún sentido? ¿diverge?

La noción más fructífera de estabilidad para un punto de equilibrio de un sistema no lineal viene dada por la siguiente definición. Supondremos que el punto de equilibrio de interés está en el origen, ya que si\(\bar{x} \neq 0\), siempre se puede aplicar una simple traducción para obtener un sistema equivalente con el equilibrio a 0.

Definición\(\PageIndex{1}\): Asymptotically Stable

Un sistema se denomina asintóticamente estable alrededor de su punto de equilibrio en el origen si satisface las siguientes dos condiciones:

1. Teniendo en cuenta alguna\(\epsilon>0, \exists \delta_{1}>0\) tal que si\(\left\|x\left(t_{0}\right)\right\|<\delta_{1}\), entonces\(\|x(t)\|<\epsilon, \forall t>t_{0}\).
2. \(\exists \delta_{2}>0\)tal que si\(\left\|x\left(t_{0}\right)\right\|<\delta_{2}\), entonces\(x(t) \rightarrow 0\) como\(t \rightarrow \infty\).

La primera condición requiere que la trayectoria del estado pueda ser confinada a una “bola” arbitrariamente pequeña centrada en el punto de equilibrio y de radio\(\epsilon\), cuando se libera de una condición inicial arbitraria en una bola de radio suficientemente pequeño (pero positivo)\(\delta_{1}\). Esto se llama estabilidad en el sentido de Lyapunov (I.s.l.). Es posible tener estabilidad en el sentido de Lyapunov sin tener estabilidad asintótica, en cuyo caso nos referimos al punto de equilibrio como marginalmente estable. También existen sistemas no lineales que satisfacen el segundo requisito sin ser estables I.s.l., como muestra el siguiente ejemplo. Un punto de equilibrio que no es estable I.s.l. se denomina inestable

Ejemplo\(\PageIndex{1}\): Unstable Equilibrium Point That Attracts All Trajectories

Considere el sistema de segundo orden con variables de estado\(x_{1}\) y\(x_{2}\) cuya dinámica se describe más fácilmente en coordenadas polares a través de las ecuaciones

\ [\ begin {align}
\ punto {r} &=r (1-r)\\ [4pt]
\ punto {\ theta} &=\ sin ^ {2} (\ theta/2)\ etiqueta {13.3}
\ end {align}\]

donde el radio\(r\) está dado por\(r=\sqrt{x_{1}^{2}+x_{2}^{2}}\) y el ángulo\(\theta\) por\(0 \leq \theta= \arctan \left(x_{2} / x_{1}\right)<2 \pi\). (Puede intentar obtener una descripción estado-espacio que involucre directamente\(x_{1}\) y\(x_{2}\).) Es fácil ver que precisamente hay dos puntos de equilibrio: uno en el origen, y el otro en\(r = 1, \theta = 0\). Te dejamos para verificar con cálculos aproximados (o simulación por computadora a partir de diversas condiciones iniciales) que las trayectorias del sistema tienen la forma mostrada en la siguiente figura.

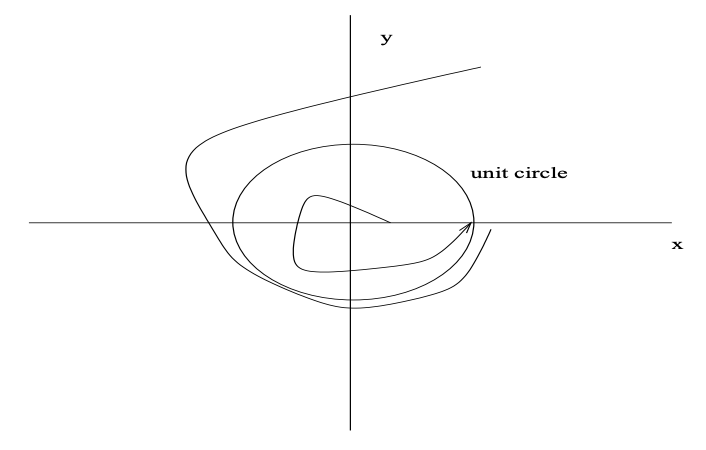
Figura\(\PageIndex{1}\): Trayectorias del sistema

Evidentemente todas las trayectorias (excepto la trivial que inicia y permanece en el origen) terminan en\(r = 1, \theta = 0\). Sin embargo, este punto de equilibrio no es estable I.s.l., porque estas trayectorias no pueden limitarse a una bola arbitrariamente pequeña alrededor del punto de equilibrio cuando son liberadas de puntos arbitrarios con cualquier bola (por pequeña que sea) alrededor de este equilibrio.