19.5: Ejercicios

Ejercicio 19.1

Supongamos que\(P(s)=\frac{a}{s}\) está conectado con un controlador\(K(s)\) en una configuración de retroalimentación unitaria. ¿Existe\(K\) tal que el sistema sea estable para ambos\(a = 1\) y\(a = -1\).

Ejercicio 19.2

Para\(P (s)\) y\(K(s)\) dado por

\[P(s)=\frac{1}{(s+2)(s+a)}, \quad K(s)=\frac{1}{s}\nonumber\]

encontrar el rango de\(a\) tal que el sistema de bucle cerrado con\(P\) y\(K\) es estable.

Ejercicio 19.3

\(P\)Déjese dar por:

\[P(s)=(1+W(s) \Delta(s)) P_{0}\nonumber\]

donde

\[P_{0}(s)=\frac{1}{s-1}, \quad W(s)=\frac{2}{s+10}\nonumber\]

y\(\Delta\) es arbitraria estable con\(\|\Delta\|_{\infty} \leq 2\). Encuentre una ganancia del controlador\(K(s) = k\) (constante) tal que el sistema sea estable. Compute todas las ganancias posibles de este tipo.

Ejercicio 19.4

Encuentre la condición de estabilidad y robustez para el conjunto de planta descrito por:

\[P=\left\{\frac{P_{0}}{1+\Delta W P_{0}}, \quad\|\Delta\|_{\infty} \leq 1\right\}\nonumber\]

Asumir que\(WP_{0}\) es estrictamente apropiado para el bien posedness.

Ejercicio 19.5

Supongamos

\[P(s)=\frac{1}{s-a} \text { and } \quad \mathrm{K}(\mathrm{s})=10\nonumber\]

están conectados en configuración de retroalimentación estándar. Si bien es fácil en este caso calcular el margen de estabilidad exacto como\(a\) cambios, en general, tales problemas son difíciles de resolver cuando hay muchos parámetros. Un enfoque es integrar el problema en un problema de estabilización robusta con dinámicas sin modelar y derivar la condición de robustez de estabilidad apropiada. Claramente, lo último proporciona un límite conservador sobre\(a\) el que el sistema se mantiene estable.

(a) Encontrar el rango exacto\(a\) para el cual el sistema es estable.

(b) Supongamos que la planta nominal es\(P_{0}=\frac{1}{s}\). Espectáculo que\(P\) pertenece al conjunto de plantas:

\[\Omega=\left\{P=\frac{P_{0}}{1+W \Delta P_{0}},\|\Delta\|_{\infty} \leq 1\right\}\nonumber\]

y\(W = -a\).

(c) Derivar una condición en el sistema de bucle cerrado que garantice la estabilidad del conjunto\(\Omega\). ¿Cómo constriñe esta condición\(a\)? ¿Esto es diferente a la parte (a)?

(d) Repetir con planta nominal\(P_{0}=\frac{1}{s+100}\)

Ejercicio 19.6

Que un modelo sea dado por la planta estable:

\[P_{0}(z)=\frac{1}{z^{-1}-\left(1+a_{0}\right)}, \quad 1>>a_{0}>0\nonumber\]

Considere la clase de plantas dada por:

\[\Omega=\left\{(z)=\frac{1}{z^{-1}-(1+b)} \mid-2 a_{0} \leq b \leq 2 a_{0}\right\}\nonumber\]

1. ¿Se\(\Omega\) puede incrustar el conjunto en un conjunto de perturbaciones acotadas por norma aditiva o multiplicativa, con planta nominal\(P_{0}\)? Muestra cómo o explica tu respuesta.
2. Si su respuesta a la parte anterior es NO, demuestre que la clase se\(\Omega\) puede incrustar en algún otro conjunto más grande caracterizado por perturbaciones delimitadas por normas. Dar una condición suficiente para la estabilidad usando el teorema de pequeña ganancia.
3. Mejora tu condición anterior para que capte el hecho de que lo desconocido es un parámetro real. (¡La condición no tiene por qué ser necesaria, pero aún debe tomar en consideración la información de fase!).

Ejercicio 19.7

Considera el Ejercicio 17.4. Supongamos que debido a problemas de implementación (por ejemplo, efectos de cuantificación), el controlador real se puede modelar como:

\[K_{a}=(I-K W \Delta)^{-1} K\nonumber\]

donde\(W\) es un filtro estable fijo, y\(\Delta\) es una perturbación estable de\(\mathcal{H}_{\infty}\) -norma menor que 1, pero por lo demás arbitraria. Proporcionar una condición no conservadora para la robustez de estabilidad del sistema de bucle cerrado. Utilice la parametrización de\(K\) en términos de\(Q\) para expresar su condición en función de\(P\) y\(Q\).

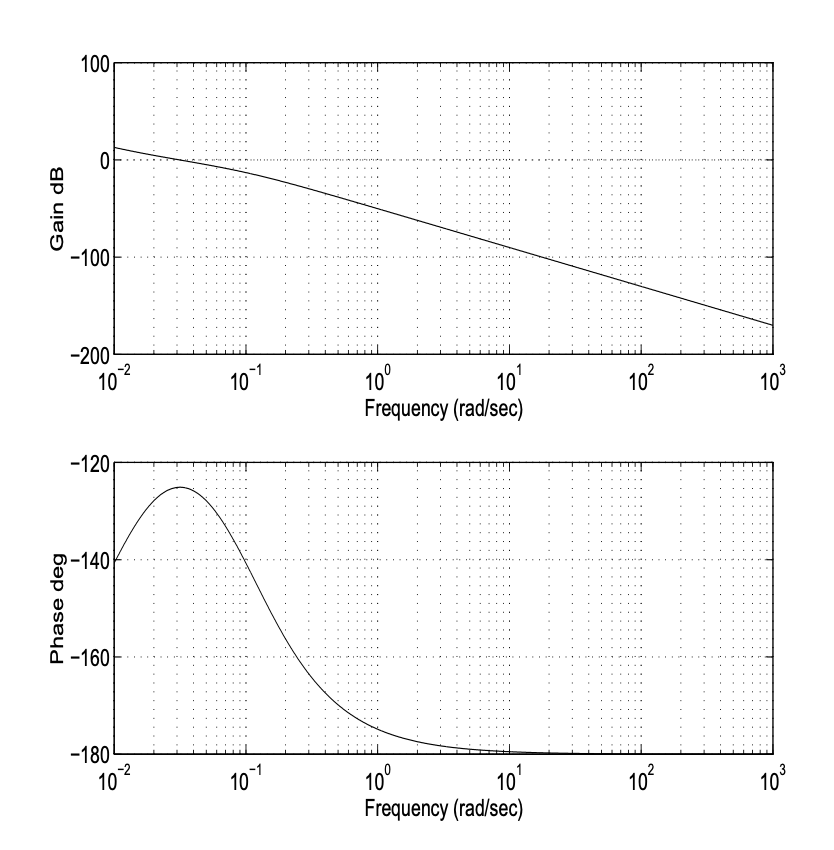
Figura 19.13: Ganancia de bucle\(P_{0} K_{1}\)