19.4: Estabilidad Robusta

En esta sección mostraremos cómo podemos analizar la estabilidad de un sistema de retroalimentación cuando la planta es incierta y se sabe que pertenece a un conjunto de la forma que describimos anteriormente. Comenzaremos con el caso de las pertubaciones aditivas. Considere la configuración de retroalimentación de unidad en la Figura 19.1. La función de transferencia de bucle abierto es\(L(s)=\left(P_{0}(s)+W(s) \Delta(s)\right) K(s)\), y

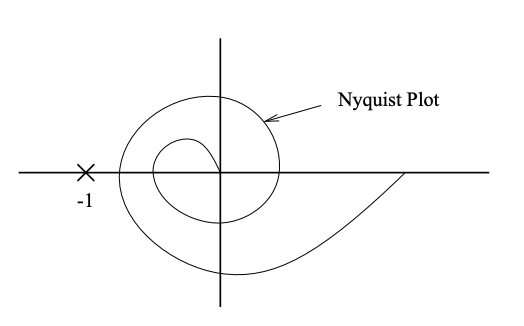
Figura 19.5: Gráfica Nyquist

la función nominal de transferencia de bucle abierto es\(L_{0}(s)=P_{0}(s) K(s)\). El sistema de retroalimentación nominal con la función de transferencia de bucle abierto nominal\(L_{0}\) es estable, ¡y queremos saber si el sistema de retroalimentación permanece estable para todos\(\Delta (s)\) satisfactorios\(|\Delta(j \omega)| \leq 1\) para todos! 2 R. Supondremos que el sistema nominal de bucle abierto es estable. Esto no provoca pérdida de generalidad y el resultado se mantiene en el caso general. Del criterio Nyquist, tenemos que la trama nyquist de\(L_{0}\) no rodea el punto\(-1\). Para el sistema perturbado, tenemos que

\ [\ comenzar {alineado}
1+L (j\ omega) &=1+P (j\ omega) K (j\ omega)\\
&=1+\ izquierda (P_ {0} (j\ omega) +W (j\ omega)\ Delta (j\ omega)\ derecha) K (j\ omega)\
&=1+L_ {0} (j\ omega) +W (j\ omega) Delta\ (j\ omega) K (j\ omega)
\ final {alineado}\ nonumber\]

De la Figura 19.6, queda claro que no\(L(\mathrm{J} \omega)\) rodeará el punto\(-1\) si se cumple la siguiente condición,

\[|W(j \omega) K(j \omega)|<\left|1+L_{0}(j \omega)\right|\nonumber\]

que se puede escribir como

\[\left|\frac{W(j \omega) K(j \omega)}{1+L_{0}(j \omega)}\right|<1 \ \tag{19.6}\]

Un argumento de ganancia pequeña

A continuación presentaremos una derivación diferente del resultado anterior que no se basa en el criterio Nyquist, y será la base para las generalizaciones multivariables de los resultados de estabilidad robusta. Dado que el sistema de retroalimentación nominal es estable, los ceros de 1 + L0 (s) están todos en la mitad izquierda del plano complejo. Por lo tanto, por la continuidad de los ceros, el sistema perturbado

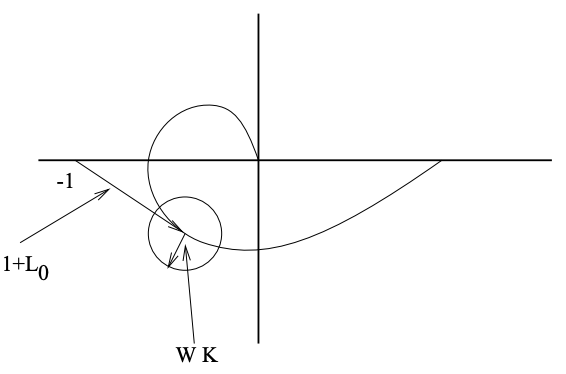
Figura 19.6: Ilustración de Gráfica Nyquist Estabilidad Robusta

será estable si y solo si

\[\left|1+\left(P_{0}(j \omega)+W(j \omega) \Delta(j \omega)\right) K(j \omega)\right|>0\nonumber\]

para todos\(\omega \in \mathbb{R},\|\Delta\|_{\infty} \leq 1\). Al reorganizar los términos, el sistema perturbado es estable si y solo si

\[\min _{|\Delta(j \omega)| \leq 1}\left|1+\frac{W(j \omega) K(j \omega)}{1+P_{0}(j \omega) K(j \omega)} \Delta(j \omega)\right|>0 \quad \text { for all } \omega \in \mathbb{R}\nonumber\]

El siguiente lema nos ayudará a transformar esta condición a la dada anteriormente.

Lema 19.1

Los siguientes son equivalentes

1. \[\min _{|\Delta(j \omega)| \leq 1}\left|1+\frac{W(j \omega) K(j \omega)}{1+P_{0}(j \omega) K(j \omega)} \Delta(j \omega)\right|>0 \quad \text { for all } \omega \in \mathbb{R}\nonumber\]
2. \[1-\left|\frac{W(j \omega) K(j \omega)}{1+P_{0}(j \omega) K(j \omega)}\right|>0 \quad \text { for all } \omega \in \mathbb{R}\nonumber\]

Prueba

Primero mostramos que 2) implica 1), lo que es consecuencia de las siguientes desigualdades

\ [\ begin {alineado}
\ izquierda|1+\ frac {W (j\ omega) K (j\ omega)} {1+P_ {0} (j\ omega) K (j\ omega)}\ Delta (j\ omega)\ derecha| &\ geq 1-\ izquierda|\ frac {W (j\ omega) K (j\ omega)} {1+P_ {0} (\ omega) K (j\ omega)}\ Delta (j\ omega)\ derecha|\\
&\ geq 1-\ izquierda|\ frac {W (j\ omega) K (j\ omega)} {1+P_ {0 } (j\ omega) K (j\ omega)}\ derecha|
\ fin {alineado}\ nonumber\]

Por lo contrario supongamos que 2) es violado, es decir existe\(\omega_{0}\) tal que

\[\left|\frac{W\left(j \omega_{0}\right) K\left(j \omega_{0}\right)}{1+P_{0}\left(j \omega_{0}\right) K\left(j \omega_{0}\right)}\right| \geq 1\nonumber\]

Escribir

\[\frac{W\left(j \omega_{0}\right) K\left(j \omega_{0}\right)}{1+P_{0}\left(j \omega_{0}\right) K\left(j \omega_{0}\right)}=a e^{j \phi}\nonumber\]

y vamos\(\bar{\Delta}\left(j \omega_{0}\right)=\frac{1}{a} e^{-j \phi-j \pi}\). Claramente,\(\left|\bar{\Delta}\left(j \omega_{0}\right)\right| \leq 1\) y

\[1+\frac{W\left(j \omega_{0}\right) K\left(j \omega_{0}\right)}{1+P_{0}\left(j \omega_{0}\right) K\left(j \omega_{0}\right)} \bar{\Delta}\left(j \omega_{0}\right)=0\nonumber\]

Ahora seleccione una perturbación racional real\(\bar{\Delta}(s)\) como

\[\bar{\Delta}(s)=\pm \frac{1}{a} \frac{s-\alpha}{s+\alpha}\nonumber\]

tal que\(\pm \frac{j \omega_{0}-\alpha}{\omega_{0}+\alpha}=e^{-j \phi-j \pi}\).

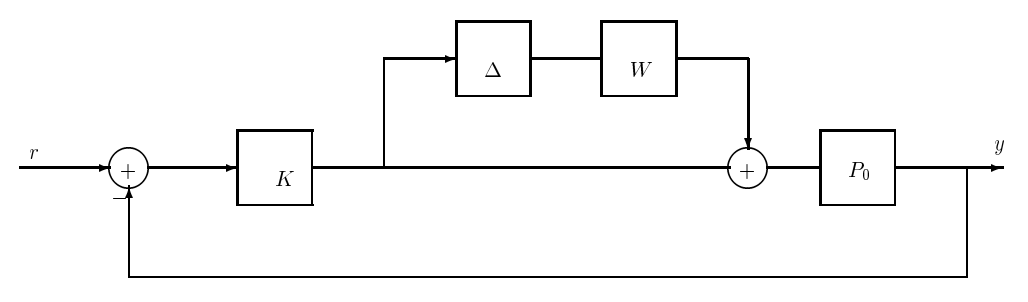
Figura 19.7: Representación de la planta real en un bucle servo a través de una perturbación multiplicativa de la planta nominal.

Se puede obtener un conjunto similar de resultados para el caso de perturbaciones multiplicativas. En particular, se puede garantizar una estabilidad robusta de la configuración de la Figura 19.7 si el sistema es estable para la planta nominal\(P_{0}\) y

\[\left|\frac{W(j \omega) P_{0}(j \omega) K(j \omega)}{1+P_{0}(j \omega) K(j \omega)}\right|<1 . \quad \text { for all } \omega \in \mathbb{R} \ \tag{19.7}\]

Ejemplo 19.3 Estabilizar un frijol

Nos interesa derivar un controlador que estabilice el haz en la Figura 19.8 y rastrea una entrada de paso (con buenas propiedades). El modelo de cuerpo rígido desde la entrada de par hasta la deflexión de la punta viene dado por

\[P_{0}(s)=\frac{6.28}{s^{2}}\nonumber\]

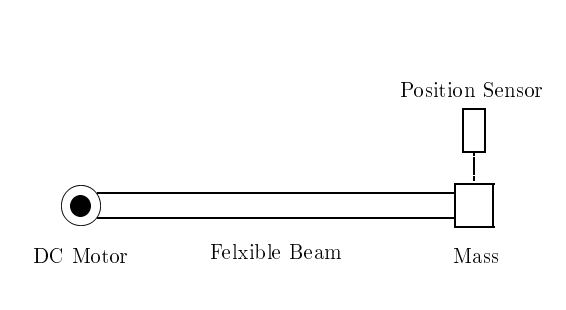
Figura 19.8: Viga Flexible.

Considera el controlador

\[K_{0}(s)=\frac{500(s+10)}{s+100}\nonumber\]

La ganancia de bucle viene dada por

\[P_{0}(s) K_{0}(s)=\frac{3140(s+10)}{s^{2}(s+100)}\nonumber\]

y se muestra en la Figura 19.9. Los polos de bucle cerrado están ubicados en -49.0, -28.6, -22.4, y la función Sensibilidad nominal viene dada por

\[S_{0}(s)=\frac{1}{1+P_{0}(s) K_{0}(s)}=\frac{s^{2}(s+100)}{s^{3}+100 s^{2}+3140 s+31400}\nonumber\]

y se muestra en la Figura 19.10. Es evidente a partir de esto que el sistema tiene buenas propiedades de rechazo de perturbaciones y rastreo. La respuesta de paso de bucle cerrado se muestra en la Figura 19.11

Si bien este controlador parece ser un diseño excelente, resulta que funciona bastante mal en la práctica. El ancho de banda de este controlador (que nunca estuvo restringido) es lo suficientemente grande como para excitar los modos flexibles del haz, los cuales no fueron tomados en cuenta en el modelo. Un modelo más complicado de la viga viene dado por

\[P_{1}(s)=\underbrace{\frac{6.28}{s^{2}}}_{\text {nominal plant }}+\underbrace{\frac{12.56}{s^{2}+0.707 s+28}}_{\text {flexible mode }}\nonumber\]

Si\(K_{0}\) está conectado a esta planta, entonces los polos de bucle cerrado son -1.24, 0.29, 0.06, -0.06, lo que implica inestabilidad.

En lugar de usar el nuevo modelo para rediseñar el controlador, nos gustaría usar el modelo nominal\(P_{0}\), y dar cuenta de los modos flexibles como dinámicas sin modelar con una cierta concentración de frecuencia. Hay varias ventajas en esto. Para

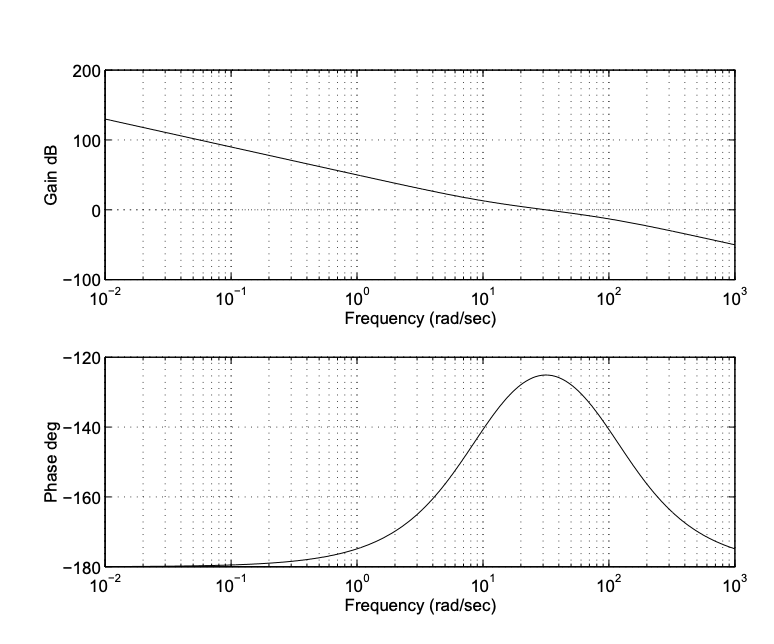
Figura 19.9: Gráfica de Bode de bucle abierto

uno, el diseño se basa en un modelo nominal más simple y por lo tanto puede resultar en un controlador más simple. Este enfoque también nos permite acomodar modos flexibles adicionales sin aumentar la complejidad de la descripción. Y finalmente, nos permite compensar el rendimiento por la robustez.

Considera el conjunto de plantas:

\[\Omega=\left\{P=P_{0}(1+\Delta) ;|\Delta(j \omega)| \leq l(\omega), \Delta \text { is stable }\right\}\nonumber\]

donde

\[l(\omega) \leq 2\left|\frac{\omega^{2}}{28-\omega^{2}+0.707 j \omega}\right|\nonumber\]

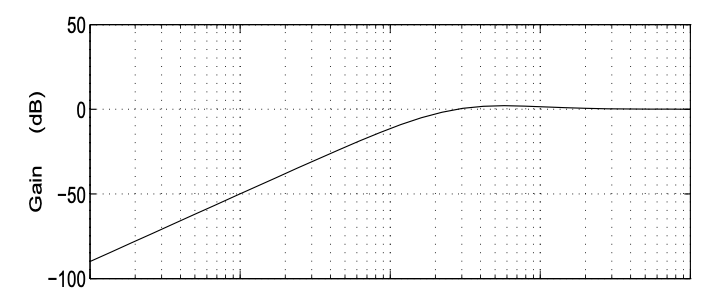
Figura 19.10: Sensibilidad nominal

Este conjunto incluye el modelo\(P_{1}\). La condición de estabilidad Robustez viene dada por:

\[|T(j \omega)|<\frac{1}{l(\omega)}\nonumber\]

Dónde\(T\) está el mapa nominal de bucle cerrado con cualquier controlador\(K\). Primero, considere el análisis de estabilidad del controlador inicial\(K_{0}(s)\). La Figura 19.12 muestra tanto la respuesta de frecuencia para\(\left|T_{0}(j \omega)\right|\) como\([l(\omega)]^{-1}\). Es evidente que se viola la condición de estabilidad y robustez ya que

\[\left|T_{0}(j \omega)\right| \nless \frac{1}{\ell(\omega)}, \quad 3 \leq \omega \leq 70 \mathrm{rad} / \mathrm{sec}\nonumber\]

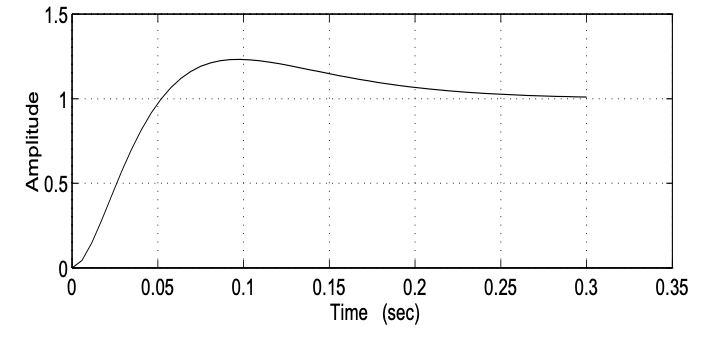
Figura 19.11: Respuesta escalonada

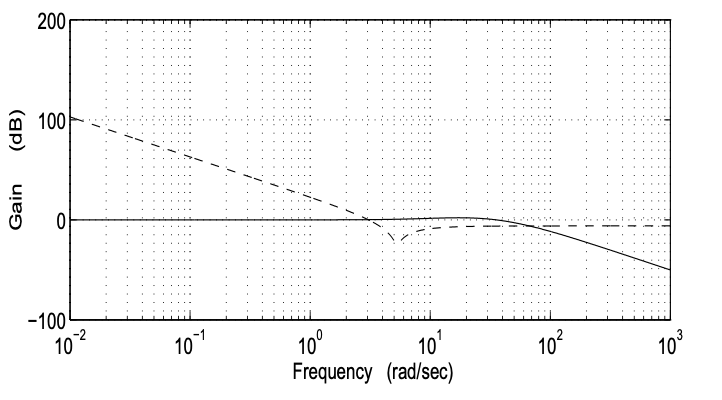
Figura 19.12:\(\left|T_{0}(j \omega)\right| \text { and }[l(\omega)]^{-1}\)

Probemos un nuevo diseño con un controlador diferente

\[K_{1}(s)=\frac{\left(5 \times 10^{-4}\right)(s+0.01)}{s+0.1}\nonumber\]

La nueva ganancia de bucle es

\[P_{0}(s) K_{1}(s)=\frac{\left(3.14 \times 10^{-3}\right)(s+0.01)}{s^{2}(s+0.1)}\nonumber\]

que se muestra en la Figura 19.13 Primero verificamos el estado de robustez con el nuevo controlador. \(T_{1}\)está dado por

\[T_{1}(s)=\frac{P_{0}(s) K_{1}(s)}{1+P_{0}(s) K_{1}(s)}\nonumber\]

La Figura 19.14 representa ambos\(\left|T_{1}(j \omega)\right|\) y\([\ell(\omega)]^{-1}\). Es claro que la condición está satisfecha. La Figura 19.15 muestra la nueva respuesta escalonada nominal del sistema. Observe que la respuesta es mucho más lenta que la derivada por el controlador\(K_{0}\). Esto se debe esencialmente al ancho de banda limitado del nuevo controlador, que era necesario para evitar la inestabilidad.