20.5: Una descripción fraccionaria lineal

Comenzamos con un modelo de planta nominal dado\(P_{0}\), y un controlador de retroalimentación\(K\) que estabiliza\(P_{0}\). La pregunta de estabilidad robusta es entonces: ¿bajo qué condiciones el controlador estabilizará todo\(P \in \Omega\)? De manera más general, suponemos que tenemos un sistema interconectado que es nominalmente estable internamente, con lo que queremos decir que la función de transferencia de una entrada agregada en cualquier entrada de subsistema a la salida observada en cualquier salida de subsistema siempre es estable en el sistema nominal. La cuestión de estabilidad robusta es entonces: bajo qué condiciones el sistema interconectado permanecerá internamente estable para todos los modelos perturbados posibles.

Si la incertidumbre de la planta se especifica (aditiva, multiplicativamente o usando una representación de retroalimentación) a través de un bloque de incertidumbre de la forma\(W \Delta\), donde\(W\) y\(\Delta\) son estables, entonces el sistema real (de bucle cerrado) se puede mapear en la configuración de retroalimentación muy simple

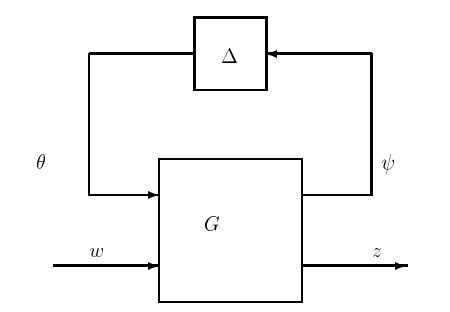
Figura 20.3: Modelo estándar para la incertidumbre.

que se muestra en la Figura 20.3. (La generalización a un bloque de incertidumbre de la forma\(W_{1} \Delta W_{2}\) es trivial, y se omite aquí para evitar la notación adicional).

Al igual que en la subsección anterior, las señales\(\psi\) y\(\theta\) respectivamente denotan la entrada y salida del bloque de incertidumbre. La entrada\(w\) se agrega en algún punto accesible arbitrario del sistema interconectado, y\(z\) denota una salida tomada de un punto accesible arbitrario. Un punto accesible en nuestra terminología es simplemente alguna entrada o salida de subsistema en el sistema real o perturbado; la entrada\(\psi\) y salida\(\theta\) del bloque de incertidumbre no calificaría como puntos accesibles.

Si eliminamos el bloque de perturbación\(\Delta\) en la Fig. 20.3, nos quedamos con el sistema nominal de bucle cerrado, el cual es estable por hipótesis (ya que el compensador\(K\) ha sido elegido para estabilizar la planta nominal y está agrupado\(G\)). La estabilidad del sistema nominal implica que las funciones de transferencia relacionan las salidas\(\psi\) y\(z\) del sistema nominal con las entradas\(\theta\) y\(w\) son todas estables. Así, en la representación de la función de transferencia

\ [\ left (\ begin {array} {l}
\ Psi (s)\\
Z (s)
\ end {array}\ right) =\ left (\ begin {array} {cc}
M (s) & N (s)\
J (s) & L (s)
\ end {array}\ right)\ left (\ begin {array} {c}
\ Theta (s)\\
W (s)
\ end {array}\ derecha)\\ tag {20.7}\]

cada una de las matrices de transferencia\(M\)\(N\),\(J\), y\(L\) es estable

Ahora incorporando la restricción impuesta por la perturbación, a saber

\[\Theta=(\Delta) \Psi \ \tag{20.8}\]

y resolviendo para la función de transferencia\(z\) relacionada\(w\) en el sistema perturbado, obtenemos

\[G_{w z}(s)=L+J \Delta(I-M \Delta)^{-1} N \ \tag{20.9}\]

Obsérvese que\(M\) es la función de transferencia “vista” por la perturbación\(\Delta\), desde la entrada\(\theta\) que impone al resto del sistema, hasta la salida\(\psi\) que mide del resto del sistema. Recordando eso\(w\) y\(z\) denotado entradas y salidas arbitrarias en los puntos accesibles del sistema de bucle cerrado real, vemos que la estabilidad interna del sistema de bucle cerrado real (es decir, perturbado) requiere que la función de transferencia anterior sea estable para todos los permitidos\(\Delta\).