5.1: Introducción a las estadísticas de corto plazo

Última actualización
Guardar como PDF

Page ID: 84293

Franz S. Hover & Michael S. Triantafyllou
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El espectro contiene información sobre la magnitud de cada componente de frecuencia en un proceso aleatorio estacionario y ergódico. Una suma de funciones armónicas con fase aleatoria satisface ergodicidad y estacionariedad, y este será un modelo dominante de un proceso aleatorio en nuestra discusión. Además, el teorema del límite central establece que un proceso aleatorio de suficiente longitud y tamaño de conjunto tiene una distribución gaussiana.

El cálculo primario es la multiplicación en el dominio de la frecuencia de un espectro de entrada por una magnitud de función de transferencia al cuadrado, para obtener el espectro de salida. Además, una entrada gaussiana que impulsa un sistema LTI creará una salida gaussiana. Lo más importante es que los espectros de entrada y salida tienen información estadística que podremos integrar en el proceso de diseño del sistema. En esta sección, nos centramos en las estadísticas a corto plazo, es decir, aquellas que se aplicarán a un proceso aleatorio que es verdaderamente estacionario. Un ejemplo fácil es un campo de olas oceánicas: en el transcurso de minutos u horas, el proceso es estacionario, pero a lo largo de los días los efectos de tormentas distantes cambiarán las estadísticas.

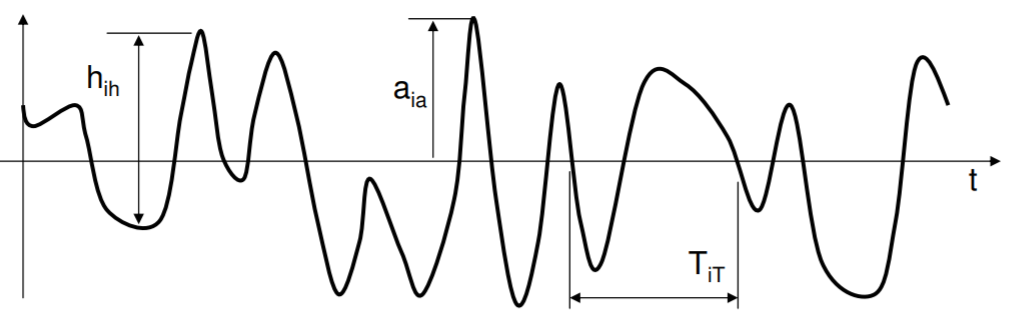
Considerando “eventos” específicos dentro de un proceso aleatorio, varios de los más importantes son la amplitud\(a_{i_a}\), la altura\(h_{i_h}\) y el período\(T_{i_T}\). El índice aquí está contando a través del registro el número de mediciones de amplitud, mediciones de altura y mediciones de período. En la siguiente figura, el periodo se mide específicamente entre cruces descendentes cero, y la amplitud es el valor máximo alcanzado después de un cruce ascendente y antes del siguiente cruce descendente. La altura va desde el mínimo después de un cruce descendente cero hasta el máximo después del siguiente cruce ascendente cero. Estas definiciones tienen que aplicarse de manera consistente, porque a veces (como se muestra) hay fluctuaciones que no cruzan sobre la línea cero.

Ejemplos de encontrar amplitud, altura y período dentro de una gráfica de espectro. — Figura\(\PageIndex{1}\): gráfica de un espectro con el período\(T_{i_T}\) medido entre cruces descendentes cero, la altura\(h_{i_h}\) medida desde el mínimo después de un cruce descendente por cero hasta el máximo después del siguiente cruce ascendente cero, y la amplitud\(a_{i_a}\) medida como el valor máximo alcanzado después de un cruce ascendente y antes del siguiente cruce descendente.

Nos centraremos en las estadísticas de la amplitud\(a\); el espectro utilizado a continuación es el de\(a\). Definamos tres momentos pares:

\ begin {align} M_0\, &=\ int\ límites_ {0} ^ {\ infty} S^+ (\ omega)\, d\ omega\\ [4pt] M_2\, &=\ int\ límites_ {0} ^ {\ infty}\ omega^2 S^+ (\ omega)\, d\ omega\ [4pt] M_4\, &=\ int\ límites_ {0} ^ {\ infty}\ omega^4 S^+ (\ omega)\, d\ omega. \ end {align}

Ya sabemos que\(M_0\) está relacionado con la varianza del proceso. Sin pruebas, estos se combinan en un parámetro de “ancho de banda” que utilizaremos pronto:

\[ \epsilon ^2 = 1 - \dfrac{M_2 ^2}{M_o M_4}. \]

Físicamente,\(\epsilon\) está cerca de 1 si hay muchos mínimos y máximos locales entre cruces por cero (banda ancha), mientras que está cerca de cero si solo hay un máximo después de un cruce ascendente por cero antes de volver a cero (banda estrecha).