6.4: Ondas Lineales

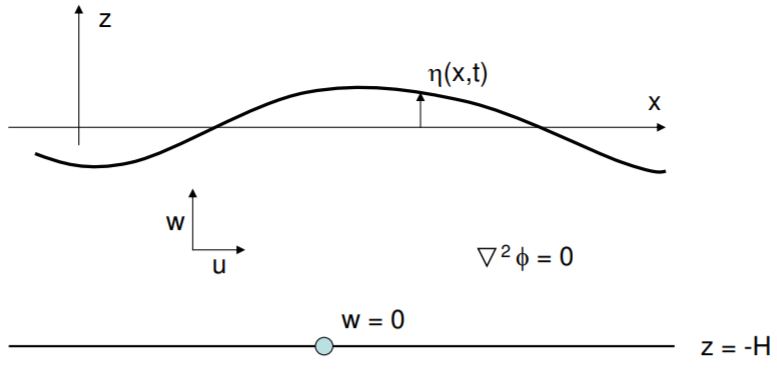
Consideramos ondas de pequeña amplitud en dos dimensiones\(x\) y\(z\), y llamamos a la deflexión superficial\(\eta(x, \, t)\), positivas en la\(z\) dirección positiva. Dentro del fluido, se mantiene la conservación de la masa, y en la superficie asumiremos que\(p = p_a\), la presión atmosférica, que podemos tomar como cero ya que es meramente un desplazamiento a todas las presiones bajo la superficie. En el fondo marino, por supuesto,\(w = 0\) porque el flujo no puede entrar y salir del límite; al mismo tiempo, debido a la suposición de flujo irrotacional, la velocidad\(u\) puede ser distinta de cero directamente al límite.

Figura\(\PageIndex{1}\): los grados de libertad disponibles para el agua en movimiento en la superficie oceánica vs. en el fondo marino.

Echando un vistazo al tamaño relativo de los términos, vemos que\((u^2 + v^2 + w^2)/2\) es mucho más pequeño que\(gz\) - considere que las ondas tienen una frecuencia de un radián por segundo más o menos, con una escala de tamaño característica (vertical) de un metro, mientras que por supuesto\(g\) es orden diez. De ahí que la ecuación de Bernoulli cerca de la superficie se simplifique para:

\[ \rho \dfrac{\partial \phi}{\partial t} + \rho g \eta \approx 0 \textrm{ at } z = 0. \]

A continuación, observamos el simple hecho de nuestras definiciones de que

\[ \dfrac{\partial \eta}{\partial t} \approx \dfrac{\partial \phi}{\partial z} \textrm{ at } z = 0. \]

En palabras, la tasa temporal de cambio de la elevación de la superficie es la misma que la\(z\) derivada del potencial, a saber\(w\). Combinando estas dos ecuaciones obtenemos

\[ \dfrac{\partial^2 \phi}{\partial t^2} + g \dfrac{\partial \phi}{\partial z} = 0 \textrm{ at } z = 0. \]

La solución para la superficie es una onda viajera

\[ \eta(x, \, t) = a \cos (\omega t - kx + \psi), \]

donde\(a\) es amplitud,\(\omega\) es la frecuencia,\(k\) es el número de onda (ver más abajo), y\(\psi\) es un ángulo de fase aleatorio. La ola viajera tiene velocidad\(\omega / k\). El potencial candidato correspondiente es

\ begin {align}\ phi (x,\, z,\, t)\, &=\, -\ dfrac {a\ omega} {k}\ dfrac {\ cosh (k (z+h))} {\ sinh (kH)}\ sin (\ omega t - kx +\ psi),\ textrm {donde}\\ [4pt]\ omega\, =\, 2\ pi/T\, =\,\ sqrt {kg\ tanh (kH)}\ textrm {(dispersión),}\\ [4pt] k\, &=\, 2\ pi/\ lambda. \ end {align}

Aquí\(\lambda\) está la longitud de onda, la extensión horizontal entre crestas. Confirmemos que este potencial satisface los requisitos. Primero, ¿resuelve la ecuación de Bernoulli en\(z = 0\)?

\ begin {align}\ dfrac {\ parcial^2\ phi} {\ parcial t^2}\, &=\,\ dfrac {a\ omega^3} {k}\ dfrac {1} {\ tanh kH}\ sin (\ omega t - kx +\ psi)\\ [4pt] &=\, a\ omega g\ sin (\ omega t - x +\ psi)\ textrm {y}\\ [4pt]\ dfrac {\ parcial\ phi} {\ parcial z}\, &=\, -a\ omega\ sin (\ omega t - kx +\ psi). \ end {align}

Claramente, la ecuación de Bernoulli en la superficie está satisfecha. Trabajando con las diversas definiciones, tenemos más

\ begin {align} u (x,\, z,\, t)\, &=\,\ dfrac {\ parcial\ phi} {\ parcial x}\, =\, a\ omega\ dfrac {\ cosh (k (z+h))} {\ sinh (kH)}\ cos (\ omega t - kx +\ psi),\\ [4pt] w (x,\, z,\, t)\, & =\,\ dfrac {\ parcial\ phi} {\ z parcial}\, =\, -a\ omega\ dfrac {\ sinh (k (z+h))} {\ sinh (kH)}\ sin (\ omega t - kx +\ psi ),\\ [4pt] p (x,\, z,\, t)\, &\ approx\, -\ rho\ dfrac {\ parcial\ phi} {\ parcial t} -\ rho gz\\ [4pt] &=\,\ rho\ dfrac {a\ omega^2} {k}\ dfrac {\ cosh (k (z+h))} {\ sinh (kH)}\ cos (\ omega t - kx +\ psi) -\ rho gz. \ end {align}

En la superficie\(z = 0\), es claro que los senos hiperbólicos en\(w(x, \, z, \, t)\) cancelan. Entonces tomar una integral a tiempo recupera fácilmente la expresión dada anteriormente para la deflexión de la superficie\(\eta(x, \, t)\). La presión aquí es\(\rho g \eta\), como se esperaría. A profundidad\(z = -H\),\(w = 0\) porque\(\sinh (0) = 0\), cumpliendo así con la condición de límite inferior. Las trayectorias de las partículas en\(x\) la dirección y la\(z\) dirección son respectivamente

\ begin {align}\ xi_p (x,\, z,\, t)\, &=\, a\ dfrac {\ cosh (k (z+h))} {\ sinh (kH)}\ sin (\ omega t - kx +\ psi)\\ [4pt]\ eta_p (x,\, z,\, t)\, &=\, d\ frac {a} {k}\ dfrac {\ cosh (k (z+h))} {\ sinh (kH)}\ cos (\ omega t - kx +\ psi). \ end {align}

De ahí que los movimientos de las partículas tomen la forma de elipses, moviéndose en sentido horario cuando la onda se mueve en\(x\) dirección positiva.

Tenga en cuenta que no hay términos no lineales\( [x, \, y, \, z, \, u, \, v, \, w, \, p, \, \phi] \) en ninguna de estas ecuaciones, y por lo tanto este modelo para ondas es lineal. En particular, esto significa que se pueden superponer ondas de diferentes frecuencias y fases, sin cambiar el comportamiento de las ondas independientes.