10.1: Momentum de una Partícula
- Page ID
- 84082
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Consideramos la dinámica del cuerpo rígido con un sistema de coordenadas fijado en el cuerpo. Desarrollaremos ecuaciones útiles para la simulación de vehículos, así como para comprender las señales medidas por una unidad de medición inercial (IMU).
Un marco común para embarcaciones, submarinos, aviones, vehículos terrestres con ruedas y otros vehículos tiene el\(x\) eje referenciado al cuerpo hacia adelante, el\(y\) eje a puerto (izquierda) y el\(z\) eje hacia arriba. Este será el sentido de nuestro sistema de coordenadas referenciadas por el cuerpo aquí.
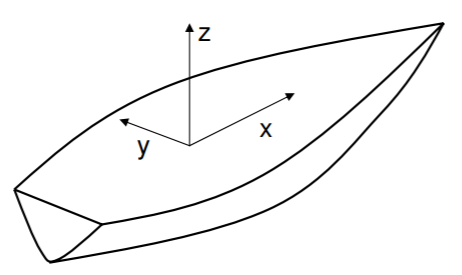.png)
Dado que el cuerpo se mueve con respecto a un marco inercial, las dinámicas expresadas en el marco referenciado al cuerpo requieren atención adicional. Primero, el impulso lineal para una partícula obedece a la igualdad\[ \vec{F} \, = \, \dfrac{d}{dt} (m \vec{v}). \]
Un cuerpo rígido consiste en una gran cantidad de estas pequeñas partículas, las cuales pueden ser indexadas. Las sumaciones que usamos a continuación pueden generalizarse a integrales con bastante facilidad. Tenemos\[ \vec{F_i} + \vec{R_i} \, = \, \dfrac{d}{dt} (m_i \vec{v}_i), \] donde\(\vec{F}_i\) está la fuerza externa que actúa sobre la partícula y\(\vec{R}_i\) es la fuerza neta ejercida por todas las demás partículas circundantes (fuerzas internas). Dado que la recolección de partículas no es separada por las fuerzas internas, debemos tener fuerzas internas iguales y opuestas de tal manera que\[ \sum_{i=1}^N \vec{R}_i \, = \, 0.\] Luego sumando todas las ecuaciones de momentum de partículas da\[ \sum_{i=1}^N \vec{F}_i \, = \, \sum_{i=1}^N \dfrac{d}{dt} (m_i \vec{v}_i). \]
Tenga en cuenta que las velocidades de las partículas no son independientes, porque las partículas están rígidamente unidas.
Ahora consideremos un marco de referencia de cuerpo, con origen \(0\), en el que la partícula\(i\) reside en el vector de radio referenciado al cuerpo\(\vec{r}\); el cuerpo se traduce y gira, y ahora consideramos cómo la ecuación de impulso depende de este movimiento.


