12.3: Diseño para Rendimiento Nominal

Última actualización
Guardar como PDF

Page ID: 84154

Franz S. Hover & Michael S. Triantafyllou
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

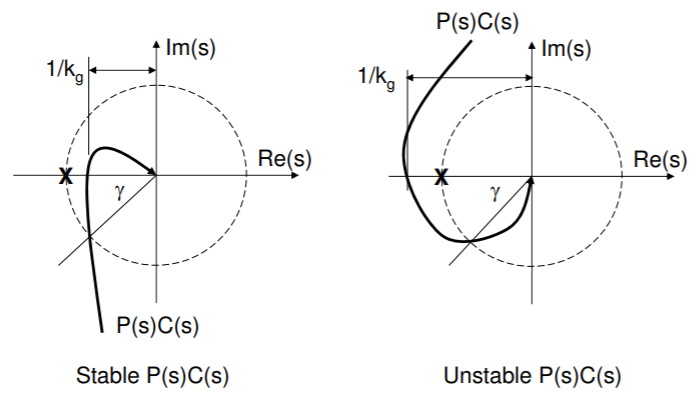
Los requisitos de rendimiento de un controlador de retroalimentación, utilizando el modelo de planta nominal, se pueden fundir en términos de la parcela de Nyquist. Dado que la función de sensibilidad mapea\(r(s)\) la entrada de referencia al error de seguimiento\(e(s)\), sabemos que\(|S(s)|\) debe ser pequeña a bajas frecuencias. Por ejemplo,

Figura comparando dos gráficas, mostrando cómo varía el valor del margen de ganancia entre una función de transferencia OL estable y una inestable. — Figura\(\PageIndex{1}\): la comparación de gráficas demuestra cómo las diferencias en el valor del margen de ganancia (\(k_g\)) determinan la estabilidad o inestabilidad de la función de transferencia OL, como se explicó en la sección anterior.

si se va a mantener el seguimiento del uno por ciento para todas las frecuencias por debajo\(\omega = \gamma\), entonces\(|S(s)| = < 0.01, \, \forall \omega < \gamma.\) Esto se puede formalizar escribiendo

\[ |W_1(s) S(s)| < 1, \]

donde\(W_1(s)\) es una función de ponderación estable de frecuencia. Para forzar\(S(s)\) a ser pequeño a bajo\(\omega\),\(W_1 (s)\) debe ser grande en el mismo rango. El requisito\(|W_1(s) S(s)| < 1\) es equivalente a\(|W_1(s)| < |1 + P(s)C(s)|\), y esta última condición puede interpretarse como: Los loci de\(P(s)C(s)\) deben permanecer fuera del disco de radio\(W_1(s)\), el cual es estar centrado en el punto crítico\((-1 + 0j)\). El disco va a ser bastante grande, posiblemente infinitamente grande, a las frecuencias más bajas.