16.5: Resolver sistemas de ecuaciones con matrices

Última actualización
Guardar como PDF

Page ID: 84065

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Un sistema de ecuaciones es cualquier conjunto de ecuaciones que comparten algunas variables. Una ecuación lineal es una ecuación que consiste enteramente en constantes y variables simples. Estas variables sólo pueden multiplicarse por una constante, y no pueden multiplicarse juntas, elevarse a un exponente, utilizarse en troncos o raíces cuadradas, o pasar por otras funciones matemáticas más complejas. A continuación se proporciona un ejemplo de un sistema de ecuaciones lineales.

\[ F_{AX} + F_{BX} = 0 \]

\[ F_{AY} - 8 = 0 \]

\[ -16 + 4 F_{AY} + 8 F_{AX} = 0 \]

En cursos como la estática y la dinámica, a menudo terminaremos con un sistema de ecuaciones lineales y se nos pedirá que resolvamos las incógnitas en esas ecuaciones. Cuando tenemos solo algunas ecuaciones en nuestro sistema, generalmente resolveremos las ecuaciones a mano usando métodos algebraicos como la sustitución o eliminación a través de la suma o la resta. Para problemas más grandes y complejos, podemos terminar con sistemas de ecuaciones más grandes y en algún momento las matemáticas pueden llegar a ser difíciles de manejar a mano. Para estos grandes sistemas de ecuaciones lineales, la forma más fácil de resolver para las incógnitas es convertir el sistema de ecuaciones en una sola ecuación matricial, y luego usar herramientas informáticas para resolver la ecuación matricial para incógnitas. Algunas herramientas informáticas te permitirán ingresar al sistema de ecuaciones manualmente, pero en segundo plano la computadora probablemente solo la esté convirtiendo en una ecuación matricial en segundo plano. Por esta razón puede ser útil entender este proceso.

En cuanto a los supuestos, es importante mencionar que este método sólo funcionará con sistemas de ecuaciones lineales, y para tener una ecuación matricial resoluble necesitaremos tener el mismo número de ecuaciones que las variables desconocidas. Por ejemplo, arriba tenemos un sistema de ecuaciones con tres ecuaciones y tres variables desconocidas. Si estos números no coinciden no podremos resolver la ecuación matricial utilizando el método que se describe a continuación.

Conversión de un Sistema de Ecuaciones en una Ecuación Matriz:

El primer paso para convertir un sistema de ecuaciones en una ecuación matricial es reorganizar las ecuaciones en un formato consistente. Generalmente pondremos todas las variables con sus coeficientes en un lado de la ecuación y las constantes en el otro lado de la ecuación. Adicionalmente, es mejor enumerar las variables en el mismo orden en cada ecuación. Este proceso de reorganización de las ecuaciones hará más fácil la conversión más adelante.

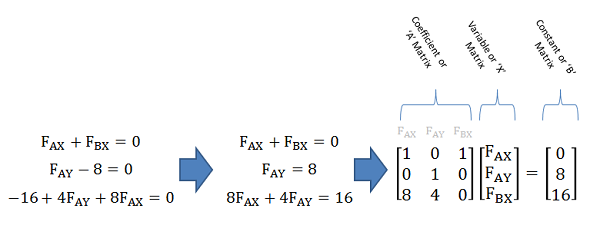
Las ecuaciones 1-3 de arriba se reescriben para que para cada ecuación, todas las variables se recojan en el lado izquierdo de la ecuación mientras que las constantes están en el lado derecho. Luego se reescribe el lado izquierdo de cada ecuación, con los coeficientes como una fila de una matriz de 3 por 3 (llamada matriz de coeficientes, o matriz A). La columna más a la izquierda de la matriz A contiene coeficientes de la variable F_AX, la columna media contiene coeficientes de la variable F_AY y la columna más a la derecha contiene coeficientes de la variable F_BX. La matriz A se multiplica por Matrix X, la matriz variable, que consiste en una matriz de 3 por 1 con las entradas F_AX, F_AY y F_BX de arriba a abajo. El producto de las matrices A y X es igual a la Matriz B, la matriz constante, que es una matriz de 3 por 1. Las entradas en la Matriz B son los lados derechos de las versiones reescritas de las Ecuaciones 1-3, con cada fila alineada con la fila de los coeficientes correspondientes en la Matriz A. — Figura\(\PageIndex{1}\): Para convertir un sistema de ecuaciones en una ecuación de matriz única, primero reorganizaremos las ecuaciones para un orden consistente. Después escribiremos las\(B)\) matrices coeficiente (\(A\)), variable (\(X\)) y constante (.

A continuación iniciaremos el proceso de redacción de las tres matrices que conforman la ecuación matricial. Estas tres matrices son la matriz de coeficientes (a menudo denominada\(A\) matriz), la matriz variable (a menudo denominada\(X\) matriz) y la matriz constante (a menudo denominada\(B\) matriz).

La matriz de coeficientes (o\(A\) matriz) es una\(N \times N\) matriz (donde\(N\) está el número de ecuaciones/número de variables desconocidas) que contiene todos los coeficientes para las variables. Cada fila de la matriz representa una sola ecuación mientras que cada columna representa una sola variable (a veces es útil escribir la variable en la parte superior de cada columna). Para instancias donde una variable no aparece en una ecuación, asumimos un coeficiente de 0.
La matriz variable (o\(X\) matriz) es una\(N \times 1\) matriz que contiene todas las variables desconocidas. Es importante que el orden de las variables en la matriz de coeficientes coincida con el orden de las variables en la matriz de variables.
Finalmente, en el otro lado del signo igual tenemos la matriz constante (o\(B\) matriz). Esta es una\(N \times 1\) matriz que contiene todas las constantes del lado derecho de las ecuaciones. Es importante que el orden de las constantes coincida con el orden de ecuaciones en la matriz de coeficientes.

Una vez que tenemos las tres matrices establecidas, estamos listos para resolver las incógnitas en la matriz variable.

Resolviendo la ecuación matricial:

Comenzando con nuestras\(B\) matrices\(A\)\(X\), y en la ecuación matricial a continuación, estamos buscando resolver para los valores de las variables desconocidas que están contenidas en nuestra\(X\) matriz.

\[ [A][X] = [B] \]

Para una ecuación escalar, simplemente haríamos esto dividiendo ambos lados por\(A\), donde\(X\) estaría el valor para\(B/A\). Con una ecuación matricial, en cambio necesitaremos múltiples ambos lados de la ecuación por la inversa de la\(A\) matriz. Esto cancelará la\(A\) matriz en el lado izquierdo, dejando solo la\(X\) matriz que estás buscando. A la izquierda tendremos el inverso de la\(A\) matriz multiplicado por la\(B\) matriz. El resultado de esta operación será una\(N \times 1\) matriz que contiene la solución para todas las variables. El valor en cada fila de la solución corresponderá a la variable listada en la misma fila de la\(X\) matriz.

\[ [X] = [A]^{-1} [B] \]

Es posible encontrar el inverso de la\(A\) matriz a mano y luego multiplicarlo con la\(B\) matriz, pero este proceso tardaría más que solo resolver las ecuaciones usando álgebra. La verdadera fortaleza del método es que las herramientas informáticas como MATLAB o Wolfram Alpha pueden realizar la inversión y multiplicación de matrices por usted.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/ZLaeFbqR9QU.

Ejemplo\(\PageIndex{1}\)

Las ecuaciones de equilibrio para el cuerpo que se muestran a continuación se enumeran a la derecha. Convierte el sistema de ecuaciones en una sola ecuación matricial y resuelve las incógnitas.

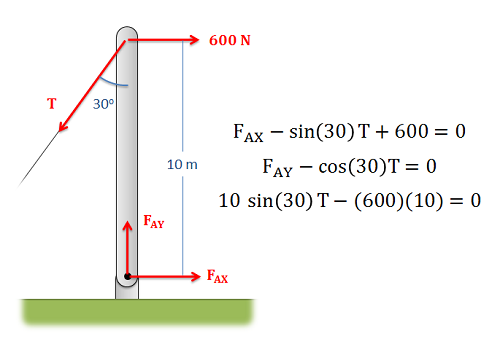
Un polo vertical de 10 metros de largo experimenta dos fuerzas en su extremo superior: una fuerza hacia la derecha de 600 N y una fuerza de tensión T a lo largo de un cable que corre hacia abajo y hacia la izquierda del extremo superior del poste a 30° de la vertical. El extremo inferior del poste experimenta una fuerza hacia la derecha de F_AX y una fuerza hacia arriba de F_AY. Tres ecuaciones describen las fuerzas sobre el cuerpo en equilibrio. Ecuación 1: F_AX - sin (30°) T + 600 = 0. Ecuación 2: F_AY - cos (30°) T = 0. Ecuación 3:10 sin (30) T - (600) (10) = 0. — Figura\(\PageIndex{2}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un sistema de ecuaciones a resolver para las fuerzas experimentadas por un poste vertical unido al suelo.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/QX-hJhXTEe0.