16.4: Productos cruzados

Última actualización
Guardar como PDF

Page ID: 84048

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El producto cruzado es una operación matemática que se puede realizar en cualquiera de dos vectores tridimensionales. El resultado de la operación de producto cruzado será un tercer vector que es perpendicular a ambos vectores originales y tiene una magnitud del primer vector multiplicada por la magnitud del segundo vector por el seno del ángulo entre los vectores.

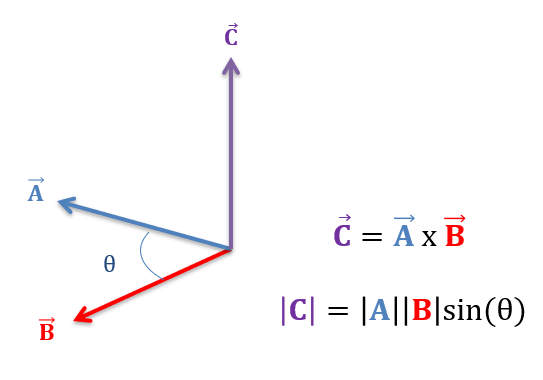
Dos vectores A y B se encuentran en el plano del “suelo”. Sus colas se ubican en el mismo punto, formando un ángulo de theta entre ellas, y el vector A apunta hacia la izquierda y hacia la pantalla mientras que el vector B apunta hacia la izquierda y ligeramente fuera de la pantalla. El producto cruzado de A y B es un tercer vector C que apunta hacia arriba, en el plano de la “pared” que es perpendicular al plano del “suelo”, desde el punto de intersección de A y B. — Figura\(\PageIndex{1}\): El producto cruzado de dos vectores será un vector que es perpendicular a ambos vectores originales con una magnitud de\(|\vec{A}|\)\(|\vec{B}|\) veces por el seno del ángulo entre\(\vec{A}\) y\(\vec{B}\).

Al encontrar un producto cruzado, puede notar que en realidad hay dos direcciones que son perpendiculares a ambos vectores originales. Estas dos direcciones serán exactamente en direcciones opuestas. Para encontrar cuál de estas dos direcciones usa el producto cruzado, usaremos la regla de la derecha.

Para usar la regla de la derecha, sostenga la mano derecha, apunte el dedo índice en la dirección del primer vector, gire el dedo medio hacia la dirección del segundo vector y sostenga el pulgar hacia arriba. Ahora tu pulgar debería apuntar en la dirección del vector de producto cruzado.

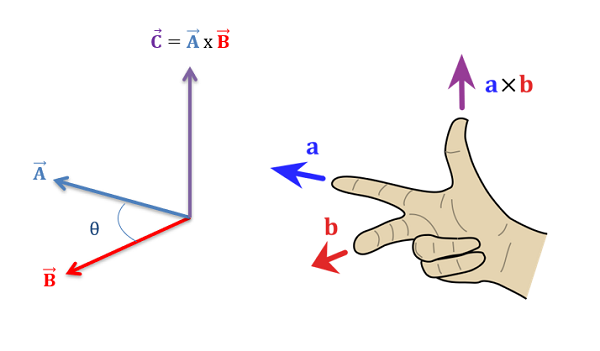
Se muestra el conjunto de vectores de la Figura 1 anterior, así como la mano derecha de una persona. El dedo índice extendido de la mano apunta en la dirección del vector A: hacia la izquierda y hacia la página. El dedo medio extendido apunta en la dirección del vector B: hacia la izquierda y ligeramente fuera de la página. El pulgar extendido apunta hacia arriba, en la dirección del vector C, o el producto de A cruz B. — Figura\(\PageIndex{2}\): Podemos usar la regla de la derecha para determinar la dirección del producto cruzado. Imagen adaptada de obra por Acdx, licencia CC-BY-SA 3.0.

Una cosa adicional que puede notar con la regla de la derecha es que cambiar el orden de los dos vectores de entrada (switching\(\vec{A}\) and\(\vec{B}\)) daría como resultado que el producto cruzado apuntara exactamente en la dirección opuesta. Esto se debe a que la operación cruzada del producto no es conmutativa, lo que significa que el orden sí importa. Específicamente, cambiar el orden de las entradas te da un resultado que es exactamente lo contrario de lo que tu cálculo original.

Cálculo del producto cruzado

Para encontrar el producto cruzado a mano, el método más sencillo es el siguiente.

Escriba las letras\(x \,\, y \,\, z \,\, x \,\, y\) seguidas como se muestra en el diagrama a continuación.
Escriba los\(z\) componentes\(x\),\(y\), y del primer vector debajo de las letras correspondientes de la fila de letras del Paso 1. Repita esto para el segundo vector, escribiendo los componentes del segundo vector en una fila debajo del primer vector.
Dibuja en diagonales como se muestra en el diagrama. Las diagonales que viajan hacia la derecha a medida que se mueven hacia abajo representan cantidades positivas, mientras que las diagonales que viajan hacia la izquierda a medida que bajan representan cantidades negativas.
Usando las letras que recorren las diagonales en la fila superior como guía para qué componente del resultado forma parte cada cantidad, tome la suma de los productos diagonales positivos y negativos para cada uno de los tres componentes del resultado. Esto debería darte la fórmula final que se muestra en el diagrama.

El vector A contiene los componentes [a, b, c] y el vector B contiene los componentes [d, e, f]. Las letras x, y, z, x, y están escritas en una fila horizontal. En una segunda fila, los componentes de A se escriben debajo de sus variables correspondientes: a, b, c, a, b. En una tercera fila, los componentes de B se escriben en el orden d, e, f, d, e. Tres líneas diagonales recorren la matriz, moviéndose de la parte superior izquierda a la inferior derecha: una pasa por x, b, f; otra a través de y , c, d; la tercera a z, a, e. Pasando de la parte superior derecha a la inferior izquierda, otras tres líneas diagonales recorren la matriz: una pasa por y, a, f; otra a través de x, c, e; la tercera a través de z, b, d. En la parte inferior del diagrama, la respuesta para el producto cruzado del vector A y el vector B se da en forma de componente [(bf-ce), (cd-af), (ae-bd)]. — Figura\(\PageIndex{3}\): Podemos utilizar la ayuda visual anterior para ayudar a recordar la fórmula para el producto cruzado.

Además de calcular el producto cruzado a mano, también podemos usar herramientas informáticas como el comando “cross” en MATLAB o herramientas basadas en web como la calculadora Wolfram Alpha Vector Operation. El acceso a estas herramientas le permite calcular de manera muy fácil y rápida el producto cruzado y es una gran ventaja al usar operaciones de vectores para analizar problemas.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/S0eav05be_U.

Ejemplo\(\PageIndex{1}\)

Calcular el producto cruzado de los vectores de fuerza\(\vec{A}\) y\(\vec{B}\) en el diagrama de abajo a mano.

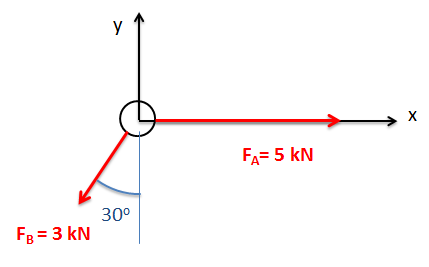
Plano de coordenadas cartesianas de orientación estándar, con dos vectores de fuerza que irradian desde el origen. El vector A tiene una magnitud de 5 kN y apunta en la dirección x positiva. El vector B tiene una magnitud de 3 kN y apunta 30° en sentido horario desde la dirección y negativa. — Figura\(\PageIndex{4}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Dos vectores de fuerza irradian desde el origen de un plano de coordenadas cartesianas.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/KQhOkEflq9s.

Ejemplo\(\PageIndex{2}\)

Calcular el producto cruzado de los vectores\(\vec{A}\) y\(\vec{B}\) en el diagrama de abajo a mano.

El vector A tiene componentes x, y, z [1, 3, 5]. El vector B tiene componentes x, y, z [6, 4, 2]. ¿Cuál es su producto cruzado? — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\).

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/oHLU_q3kVKc.

Ejemplo\(\PageIndex{3}\)

Calcular el producto cruzado de los vectores\(\vec{A}\) y\(\vec{B}\) en el diagrama siguiente usando MATLAB.

El vector A tiene componentes x, y, z [1, 3, 5]. El vector B tiene componentes x, y, z [6, 4, 2]. ¿Cuál es su producto cruzado?

Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\).

Solución:: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/a9w6GWQJ96A.

Ejemplo\(\PageIndex{4}\)

Calcule el producto cruzado de vectores\(\vec{A}\) y\(\vec{B}\) en el diagrama siguiente, usando la Calculadora de Operación de Vectores Wolfram.

Solución:: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/24JCFHWWGG4.