1.3: Descripción de la deformación en el sistema de coordenadas cilíndricas

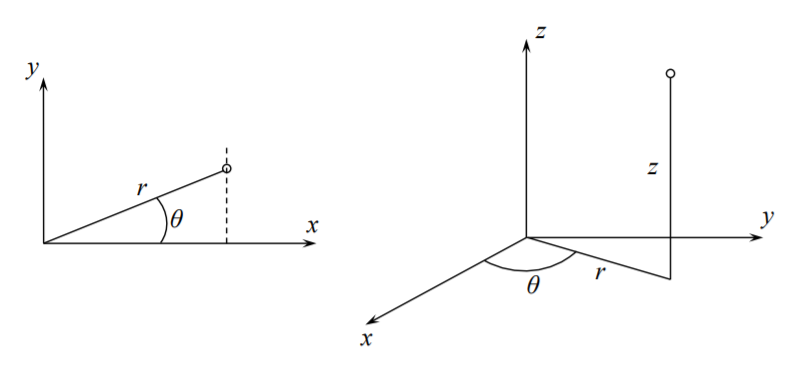
En esta sección las relaciones deformación-desplazamiento se derivarán en el sistema de coordenadas cilíndricas\((r, \theta, z)\).

El sistema de coordenadas polares es un caso especial con\(z = 0\). Los componentes del vector de desplazamiento son\(\{u_r, u_{\theta}, u_z\}\). Existen dos formas de derivar las ecuaciones cinemáticas. Dado que la deformación es un tensor, se puede aplicar la regla de transformación de una coordenada a otra. Este enfoque se sigue por ejemplo en las páginas 125-128 del libro sobre “Un primer curso en mecánica continua” de Y.C. Fung. O bien, la expresión para cada componente del tensor de deformación puede derivarse de la geometría. Aquí se adopta este último enfoque. Los componentes diagonales (normales)\(\epsilon_{rr}\)\(\epsilon_{\theta\theta}\), y\(\epsilon_{zz}\) representan el cambio de longitud de un elemento infinitesimal. Los componentes no diagonales (cizallamiento) describen el cambio de ángulos.

Figura\(\PageIndex{1}\): Sistema de coordenadas rectangular y cilíndrico.

Figura\(\PageIndex{2}\): Cambio de longitud en la dirección radial.

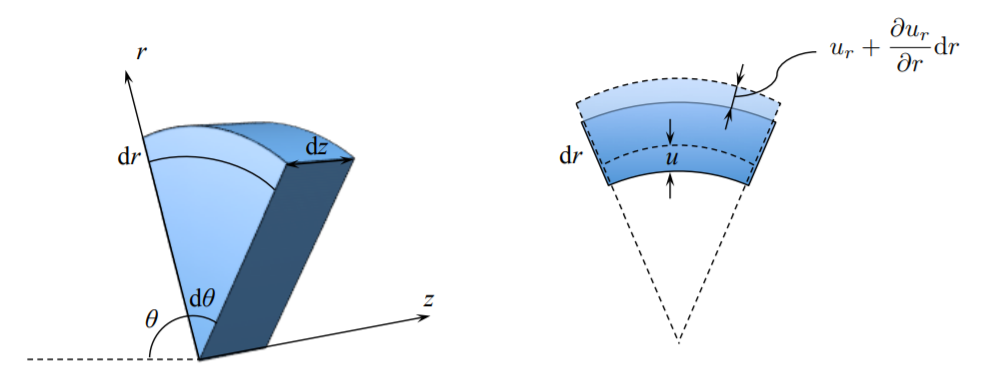
La deformación radial se debe únicamente a la presencia del gradiente de desplazamiento en la\(r\) dirección -dirección

\[\epsilon_{rr} = \frac{ \left\{ u_r + \frac{\partial u_r}{\partial r} d r - u_r \right\} }{ d r} = \frac{\partial u_r}{\partial r}\]

La deformación circunferencial tiene dos componentes

\[\epsilon_{\theta\theta} = \epsilon_{\theta\theta}^{(1)} + \epsilon_{\theta\theta}^{(2)}\]

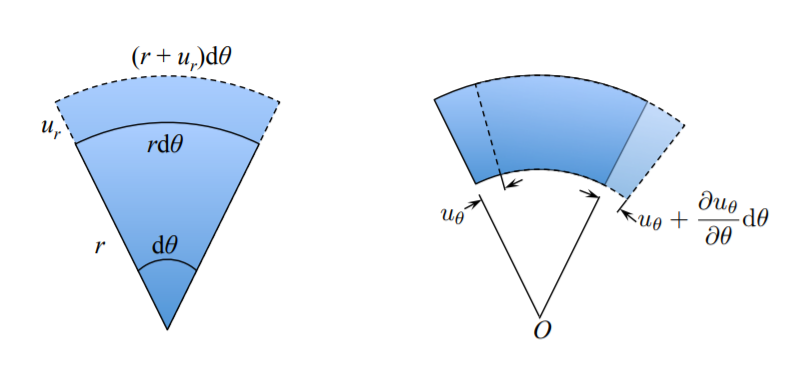
El primer componente es el cambio de longitud debido al desplazamiento radial, y el segundo componente es el cambio de longitud debido al desplazamiento circunferencial.

A partir de la Figura (\(\PageIndex{3}\)) los componentes\(\epsilon_{\theta\theta}^{(1)}\) y\(\epsilon_{\theta\theta}^{(2)}\) se calculan como

\[\epsilon_{\theta\theta}^{(1)} = \frac{(r+u_r) d \theta - r d\theta}{r d \theta} = \frac{u_r}{r}\]

\[\epsilon_{\theta\theta}^{(2)} = \frac{u_{\theta} + \frac{\partial u_{\theta}}{\partial \theta} d \theta - u_{\theta} }{r d \theta} = \frac{1}{r}\frac{\partial u_{\theta}}{\partial \theta}\]

Figura\(\PageIndex{3}\): Dos modos de deformación responsables de la deformación circunferencial (aro).

El componente circunferencial total (aro) del tensor de tensión es

\[\epsilon_{\theta \theta} = \frac{u_r}{r} + \frac{1}{r} \frac{\partial u_{\theta}}{\partial d \theta}\]

Los componentes de deformación en la\(z\) dirección -son los mismos que en el sistema de coordenadas rectangulares

\[\epsilon_{zz} = \frac{\partial u_z}{\partial z}\]

La deformación por cizallamiento\(\epsilon_{r\theta}\) describe un cambio en el ángulo recto.

Figura\(\PageIndex{4}\): Construcción que explica el cambio de ángulos por desplazamiento radial y circunferencial.

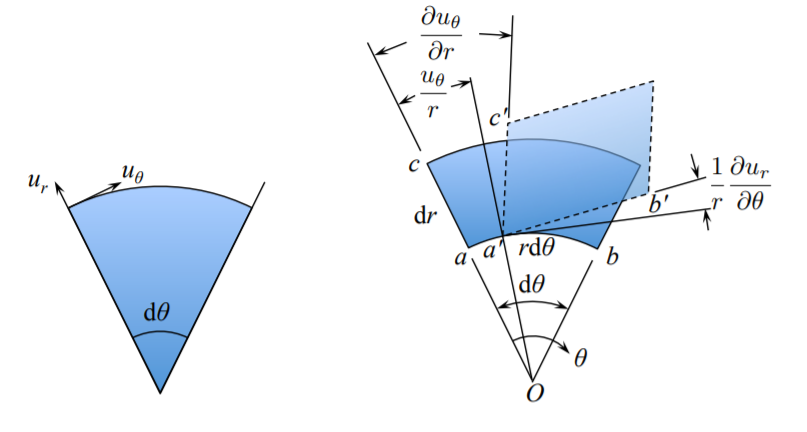
De la Figura (\(\PageIndex{4}\)) la deformación por cizallamiento sobre el\(\{r, \theta\}\) plano es

\[\epsilon_{r \theta} = \frac{1}{2} \left[ \frac{\partial u_{\theta}}{\partial r} - \frac{u_{\theta}}{r} + \frac{1}{r}\frac{\partial u_r}{\partial \theta} \right]\]

En el\(\{r, z\}\) plano, la\(\epsilon_{rz}\) cizalla se desarrolla a partir de los respectivos gradientes, ver Figura (\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): Cambio de ángulos son\(\{r, z\}\) planos.

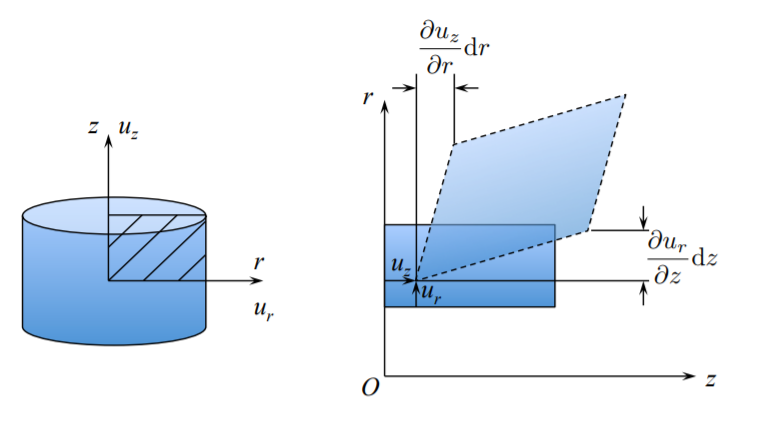
De la construcción en la Figura (\(\PageIndex{4}\)), el componente\(\epsilon_{rz}\) es

\[\epsilon_{rz} = \frac{1}{2} \left( \frac{\partial u_r}{\partial z}+ \frac{\partial u_z}{\partial r}\right)\]

Finalmente, una imagen similar es válida en el\(\{z, \theta\}\) plano (tangente)

Figura\(\PageIndex{6}\): Visualización del componente de deformación\(\epsilon_{\theta z}\).

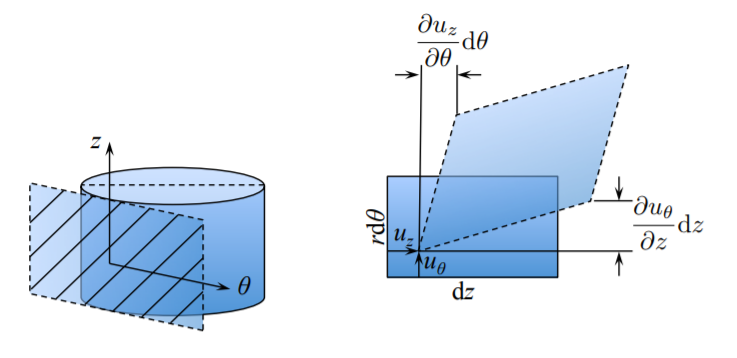
El componente\(\epsilon_{\theta z}\) del tensor de deformación es la mitad del cambio de ángulos, i.e.

\[\epsilon_{\theta z} = \frac{1}{2} \left( \frac{\partial u_z}{r \partial \theta} + \frac{\partial u_{\theta}}{\partial z}\right)\]

Para resumir la derivación, los seis componentes del tensor de deformación infinitesimal en el sistema de coordenadas cilíndrico son

\[\epsilon_{rr} = \frac{\partial u_r}{\partial r} \]

\[\epsilon_{\theta \theta} = \frac{u_r}{r} + \frac{1}{r} \frac{\partial u_{\theta}}{\partial \theta}\]

\[\epsilon_{zz} = \frac{\partial u_x}{\partial z}\]

\[\epsilon_{r \theta} = \epsilon_{\theta r} = \frac{1}{2} \left( \frac{1}{r}\frac{\partial u_r}{\partial \theta} + \frac{\partial u_{\theta}}{\partial r} - \frac{u_{\theta}}{r}\right)\]

\[\epsilon_{\theta z} = \epsilon_{z \theta} = \frac{1}{2} \left( \frac{\partial u_z}{r \partial \theta}+ \frac{\partial u_{\theta}}{\partial z}\right)\]

\[\epsilon_{zr} = \epsilon_{rz} = \frac{1}{2} \left( \frac{\partial u_r}{\partial z}+ \frac{\partial u_z}{\partial r}\right)\]

Se obtienen considerables simplificaciones en el caso de la simetría axial (rotacional para la cual\(u_{\theta} = 0\) y\(\frac{\partial}{\partial \theta} [\,] = 0\)

\[\epsilon_{rr} = \frac{\partial u_r}{\partial r} \quad \epsilon_{r \theta} = 0\]

\[\epsilon_{\theta \theta} = \frac{u_r}{r} \quad \epsilon_{\theta z} = 0\]

\[\epsilon_{zz} = \frac{\partial u_z}{\partial z} \quad \epsilon_{zr} = \frac{1}{2} \left( \frac{\partial u_r}{\partial z}+ \frac{\partial u_z}{\partial r}\right)\]

La aplicación de las relaciones geométricas anteriores para la carga axisimétrica de placas circulares y carcasas cilíndricas se dará en capítulos posteriores.