1.5: Hipótesis de Euler-Bernoulli
- Page ID
- 85198
En esta sección a menudo se hace referencia al eje de la viga. El significado del eje del haz es intuitivo para una viga prismática de sección transversal rectangular. Es el eje medio. También se utilizan frecuentemente otros términos, como: eje neutro, eje de flexión y eje centroidal. Todos expresan la misma propiedad de que no se\(\sigma_{xx}\) deben desarrollar tensiones axiales en el eje bajo flexión pura.
Hipótesis 1: El plan permanece plano
Esto se ilustra en la Figura (\(\PageIndex{1}\)) que muestra una sección transversal arbitraria de la viga antes y después de la deformación.
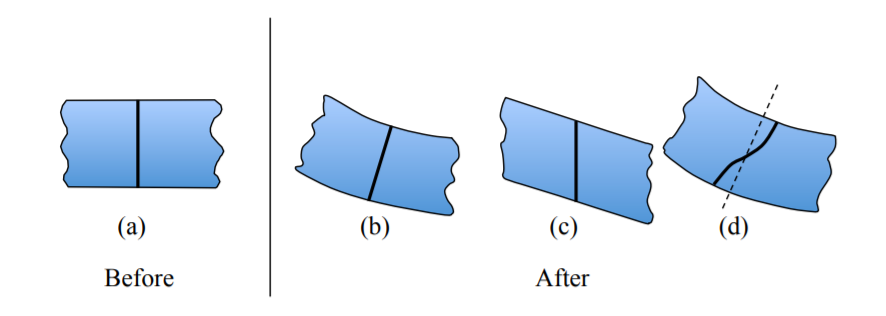
Imagina un corte recto hecho a través de la viga no deformada. La hipótesis plano-resta-plano significa que todos los puntos de material en el corte original se alinean también en un plano en la viga deformada. Los casos b) y c) obedecen a la hipótesis pero la sección deformada (d) la viola.
Hipótesis 2: Lo normal sigue siendo normal
Si el corte inicial se realizó en ángulo recto del eje de viga no deformado como en la Figura\(\PageIndex{2}\) ((a)), debe permanecer normal al eje deformado, ver Figura (\(\PageIndex{2}\)(b)).
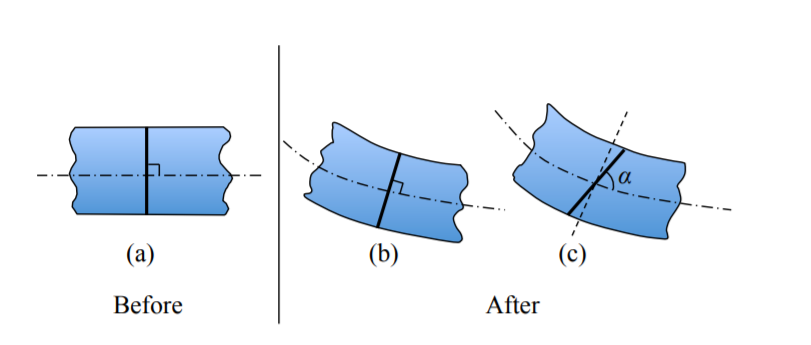
En el boceto de la Figura\(\PageIndex{2}\) ((c)) se viola la hipótesis cuando el ángulo\(\alpha \neq 90^{\circ}\).
La hipótesis de Euler-Bernoulli da lugar a una elegante teoría de las cepas infinitesimales en vigas con secciones transversales arbitrarias y carga en dos direcciones fuera del plano. El lector interesado es referido a varias monografías con un tratamiento detallado del tema, de carga biaxial de vigas. El presente conjunto de notas sobre vigas se desarrolla bajo el supuesto de deformación plana. Esto significa que el movimiento del eje del haz está restringido solo a un plano.
Matemáticamente, la Hipótesis 1 se satisface cuando el componente u del vector de desplazamiento es una función lineal de\(z\).
\[u(z) = u^{\circ} - \theta z \text{ at any x} \label{2.35}\]
El primer término constante,\(u^{\circ}\) es el desplazamiento del eje de la viga (debido a la fuerza axial). El segundo término se debe a la flexión sola, Figura (\(\PageIndex{3}\)).
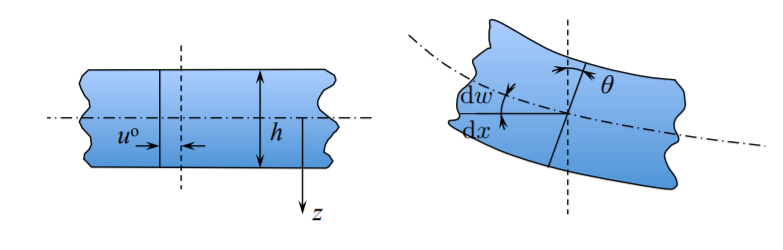
La segunda hipótesis de Euler-Bernoulli se satisface si la rotación de la sección transversal deformada\(\theta\) es igual a la pendiente local del eje medio doblado\(\frac{ d w}{ d x}\)
\[\theta = \frac{ d w}{ d x} \label{2.36}\]
Al eliminar el ángulo de rotación θ entre las ecuaciones\ ref {2.35} y\ ref {2.36} rendimientos
\[u(x, z) = u^{\circ} - \frac{ d w}{ d x}z \label{2.37}\]
Se puede observar en la Figura (\(\PageIndex{3}\)) que el desplazamiento en el lado inferior (de tracción) de la viga es negativo, lo que explica el signo menos en el segundo término de Ecuaciones\ ref {2.36} y\ ref {2.37}.
Hipótesis 3
La forma y tamaño de la sección transversal de la viga permanecen sin cambios. Esto significa que la componente vertical del vector de desplazamiento no depende de la\(z\) coordenada -. Todos los puntos de la sección transversal se mueven en la misma cantidad.
\[w = w(x) \label{2.38}\]
En el caso de la deformación plana, que cubre la mayoría de los casos prácticos de la respuesta del haz, el\(y\) componente -componente del vector de desplazamiento desaparece
\[v = 0\]
Ahora estamos en condiciones de calcular todos los componentes del tensor de deformación a partir de la Ecuación (1.2.10)
\[\epsilon_{xx} = \frac{ d u_{x}}{ d x} = \frac{ d u}{ d x}\]
\[\epsilon_{zz} = \frac{ d u_{y}}{ d y} = \frac{ d v}{ d y} = 0 \text{ on account of } \ref{2.42}\]
\[\epsilon_{zz} = \frac{ d u_{zz}}{ d z} = \frac{ d w(x)}{ d z} = 0 \text{ from } \ref{2.38}\]
\[\epsilon_{xy} = \frac{1}{2} \left(\frac{ d u_{x}}{ d y} + \frac{ d u_y}{ d x} \right) = 0 \text{ from } \ref{2.37} \text{ and } \ref{2.42}\]
\[\epsilon_{yz} = \frac{1}{2} \left(\frac{ d u_{y}}{ d z} + \frac{ d u_z}{ d y} \right) = \frac{1}{2} \left(\frac{ d v}{ d z} + \frac{ d w}{ d y} \right) = 0 \]
\[\begin{align} \epsilon_{zx} & = \frac{1}{2} \left(\frac{ d u_{z}}{ d x} + \frac{ d u_x}{ d z} \right) = \frac{1}{2} \left(\frac{ d w}{ d x} + \frac{ d u}{ d z} \right) \\ & = \frac{1}{2} \left(\frac{ d w}{ d x} - \frac{ d w}{ d x} \right) = 0 \nonumber \end{align}\]
Se observa que todos los componentes del tensor de tensión desaparecen excepto el que está en la dirección del eje de la viga.
Tenga en cuenta que\(\epsilon_{xx}\) es el único componente del tensor de deformación en la teoría del haz elemental. Por lo tanto, el subíndice “\(xx\)” se puede descartar y, a menos que se especifique lo contrario\(\epsilon_{xx} = \epsilon\). Introduciendo la ecuación\ ref {2.37} en la ecuación\ ref {2.38} se obtiene
\[\epsilon (x, z) = \frac{ d u^{\circ}(x)}{ d x} - \frac{ d ^2w(x)}{ d x^2}z\]
El primer término representa la deformación derivada de una extensión uniforme de toda la sección transversal
\[\epsilon^{\circ}(x) = \frac{ d u^{\circ}(x)}{ d x} \label{2.42}\]
El segundo término suma un aporte de flexión. Introducción a la definición de la curvatura del eje del haz
\[\kappa \buildrel \rm {def} \over{=} −\frac{ d ^2w(x)}{ d x^2},\]
la expresión para cepa se puede poner en la forma final:
\[\epsilon(x, z) = \epsilon^{\circ}(x) + z\kappa\]
Matemáticamente, la curvatura se define como un gradiente de la pendiente de una curva. El signo menos en la Ecuación (1.3.4) se desprende de la descripción rigurosa de la curvatura de una línea en el sistema de coordenadas asumido. Físicamente, asume que las tensiones en el lado de tracción de la viga son positivas. Se ofrece una interpretación bastante diferente de la hipótesis de Euler-Bernoulli al considerar una expansión de dos términos del perfil de deformación exacto en la serie Taylor alrededor del punto
\[\epsilon(x, z) = \epsilon(x, z) = |_{z=0} + \left. \frac{ d {\epsilon}}{ d z}\right|_{z=0} z + \left. \frac{1}{2}\frac{ d ^2 \epsilon} { d z^2}\right|_{z=0} z^2 + \ldots\]
Tomar solo los dos primeros términos es una buena aproximación de ingeniería pero conduce a algunas inconsistencias internas de la teoría del haz elemental. Estas inconsistencias se explicarán en los dos capítulos siguientes.


